- ビットごとの XOR 演算子とも呼ばれます。 排他的論理和
- を使用して表されます。 '^'
- 名前が示すように、それはに作用します ビットレベル オペランドの。
- ビットごとの XOR 演算子は、ビットごとの演算子のカテゴリに分類されます。
- ビットごとの排他的論理和演算子 (XOR) では 2 つのオペランドが必要で、これら 2 つのオペランドは XOR 記号 (つまり '^') で区切られます。
- 2 つのオペランドに XOR 演算子を適用した後に得られる出力または結果を決定するには、XOR 演算子の論理真理値表に従う必要があります。
- XOR 真理値表は、XOR 演算子の適切なロジックを使用して構築された数学表です。
- XOR 演算子の背後で使用されるロジックは次のとおりです。 XOR 演算が 2 つに適用されるたびに 違う 2 つのオペランドのビットの場合、結果は常に次のようになります。 「1」、 そして、XOR 演算が 2 つに適用されると、 同じ 2 つのオペランドのビットの結果が出力を生成します 「0」。
排他的論理和 (XOR) 演算子の真理値表
2 つのオペランドがあるとします。最初のオペランドが A、2 番目のオペランドが B である場合、これら 2 つのオペランドによって形成される入力の合計の組み合わせは 4 になります。次の XOR 真理値表を使用して、対応する出力を決定します。結果は C でキャプチャされます。ここでは C = A ^ B。
この真理値表では、入力をビットの形式、つまり 0 と 1 で受け取り、出力もビットの形式、つまり 0 と 1 で生成されます。
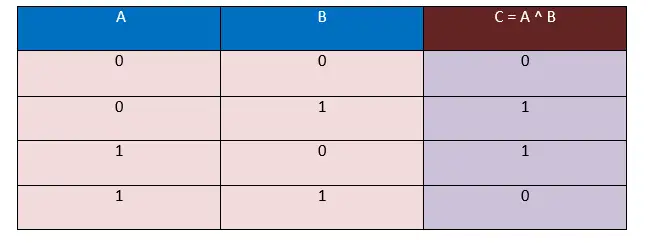
ここで、上記の XOR 真理値表では、オペランド A と B の値が異なる場合、つまり ( 0, 1 )、( 1, 0 ) の場合、出力される結果は常に 1 になることがわかります。オペランド A と B の値が同じ、つまり ( 0, 0 )、( 1, 1 ) の場合、出力される結果は常に 0 になります。
同様に、このようにして、次の真理値表を描くことができます。 ブール値 値 -
2 つのオペランドがあるとします。最初のものは あ そして2番目は B 。これら 2 つのオペランドによって形成される入力の合計の組み合わせは 4 になります。次の XOR 真理値表を使用して、対応する出力を決定します。結果は C に取り込まれます (ここでは C = A ^ B)。
この真理値表では、真理値、つまり True ( T ) と False ( F ) の形式で入力を受け取ります。出力は True 値、つまり T と F の形式でも生成されます。

ここで、上記の XOR 真理値表では、オペランド A と B の値が異なる場合、つまり ( F, T )、( T, F ) の場合、結果は常に T になることがわかります。オペランド A と B の値が同じ、つまり ( F, F )、( T, T ) の場合、結果は常に F になります。
上の表から、次のことがわかります。 T ( True ) は 1 で示され、F ( False ) は 0 で示されます。
与えられた問題を解決するための手順 -
- 問題で指定されるオペランドは常に 10 進数値になります。
- まず、オペランドの値を次のように変換する必要があります。 バイナリ
- オペランドの値を 2 進数に変換した後、両方のオペランドを重ね合わせます。
- 排他的論理和 (XOR) 演算を適用する前に、次のことを確認してください。 桁数 それらの中で。
- 桁数が一致しない場合、小さいオペランドの左端に追加の 0 が桁数のバランスをとります。
- 最後に、上記の真理値表を利用して、XOR 演算を適用するために一度に 1 ビットずつ、オペランドに 1 つずつ XOR 演算を適用します。
- 最後に、結果はアウトプットという形で生成されます。
- 生成される出力はバイナリ形式になります。バイナリ形式を 10 進数形式に変換し、結果の値を書き留めます。
C++ でのビットごとの排他的論理和 (XOR) 演算の実行
例を使用して、C++ での XOR 演算の実行について詳しく理解してみましょう。
例 1: 整数値の排他的論理和を求めます。また、それを説明し、実行コードを C++ で記述します。
解決: 上記の質問で指定された対応する 2 つのオペランド、つまり 10 と 14 を格納する 2 つの変数 ' a ' と ' b ' を考えてみましょう。
ここで、a = 10、b = 14 です。
以下の手順に従って、指定された 2 つのオペランドの排他的論理和を求めます。
- 10 と 14 は 10 進形式であることがわかっており、ビットごとの XOR 演算を適用するには、それを 2 進形式に変換する必要があります。
- バイナリ形式 ' a '、つまり 10 は 「1010」 ' b ' のバイナリ形式、つまり 14 は 「1110」。
- ここで、a に存在する 2 進数の数が 4 であり、b に存在する 2 進数の数も 4 であることがわかります。したがって、両方の変数に存在する 2 進数の数は同じであり、すでにバランスが取れているため、バランスを取るためにさらに 0 の数を追加する必要はありません。
- ここで、「b」に存在する 2 進数を「a」に存在する 2 進数に当てはめます。
- 最後に、対応するビットに XOR 演算を 1 つずつ適用して一致させ、出力を書き留めます。
- 上記の質問が 10 進数形式で示されているように、最終的に生成される出力はバイナリ形式になるため、結果を 10 進数形式に変換する必要があります。
説明:
a = 10 (10 進数形式)
b = 14 (10 進数形式)
ここで、XOR b の場合、a と b をバイナリ形式に変換する必要があります。
ランダムSQLで並べ替える
a = 1010 (バイナリ形式)
b = 1110 (バイナリ形式)
ここで、a と b に XOR 演算を適用します。
a = 1010
b = 1110
---------------
a ^ b = 0100 (バイナリ形式)
a ^ b の結果は 0100 で、これはバイナリ形式です。
結果を 10 進数形式に変換すると、4 になります。
10^14 = 4
注: 上記の XOR 真理値表を使用すると、対応するビットの出力が生成されます。
ここで、C++ 言語で 10 と 14 にビットごとの XOR 演算を適用し、結果 (つまり 4) を取得します。
上記の例の C++ コード:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> 出力

例 2: 整数値の排他的論理和を求めます。また、それを説明し、実行コードを C++ で記述します。
解決: 上記の質問で指定された対応する 2 つのオペランド、つまり 3 と 15 を格納する 2 つの変数 ' a ' と ' b ' を考えてみましょう。
ここで、a = 3、b = 15 です。
以下の手順に従って、指定された 2 つのオペランドの排他的論理和を求めます。
- 3 と 15 は 10 進形式であることがわかっており、ビットごとの XOR 演算を適用するには、それを 2 進形式に変換する必要があります。
- バイナリ形式 ' a '、つまり 3 は '十一' ' b ' のバイナリ形式、つまり 15 は 「1111」。
- ここで、a に存在する 2 進数の数が 2 であり、b に存在する 2 進数の数が 4 であることがわかります。したがって、両方の変数に存在する 2 進数の数は同じではありません。したがって、アンバランスなので、下位の 2 進数、つまり a の左側にさらに多くの 0 を追加する必要があります。これは ' 十一' 、バランスをとるために。
- バランスをとると、a の値は次のようになります。 「0011」 、b は 「1111」。
- ここで、「 b 」に存在する 2 進数を「 a 」に存在する 2 進数にまとめます。
- 最後に、対応するビットに XOR 演算を 1 つずつ適用して一致させ、出力を書き留めます。
- 上記の質問が 10 進数形式で示されているように、最終的に生成される出力はバイナリ形式になるため、結果を 10 進数形式に変換する必要があります。
説明:
a = 3 (10 進数形式)
b = 15 (10 進数形式)
ここで、XOR b の場合、a と b をバイナリ形式に変換する必要があります。
a = 0011 (バイナリ形式)
b = 1111 (バイナリ形式)
ここで、a と b に XOR 演算を適用します。
a = 0011
b = 1111
---------------
a ^ b = 1100 (バイナリ形式)
a ^ b の結果は 1100 で、これはバイナリ形式です。
結果を 10 進数形式に変換すると、12 になります。
3^15 = 12
注: 上記の XOR 真理値表を使用すると、対応するビットの出力が生成されます。
ここで、C++ 言語で 3 と 15 にビットごとの XOR 演算を適用し、結果 (12) を取得します。
上記の例の C++ コード:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> 出力

