前提条件 – データ マイニング、類似性測定は、データセット内のデータ オブジェクトの特徴を表す次元との距離を指します。この距離が小さい場合は類似度が高くなりますが、距離が大きい場合は類似度が低くなります。一般的な類似性尺度には次のようなものがあります。
- ユークリッド距離。
- マンハッタンの距離。
- ジャカードの類似性。
- ミンコフスキー距離。
- コサイン類似度。
コサイン類似度 データ オブジェクトがサイズに関係なくどの程度類似しているかを判断するのに役立つメトリックです。 Python ではコサイン類似度を使用して 2 つの文間の類似性を測定できます。コサイン類似度では、データセット内のデータ オブジェクトはベクトルとして扱われます。 2 つのベクトル間のコサイン類似度を求める公式は次のとおりです。
(x, y) = x . y / ||x|| ||y||>
どこ、
- バツ 。 y = ベクトル「x」と「y」の積（ドット）。||x|| そして ||そして|| = 2 つのベクトル「x」と「y」の長さ (大きさ)。||x||
||そして|| = 2 つのベクトル「x」と「y」の正規積。 例 ： 2 つのベクトル間の類似性を見つける例を考えてみましょう – 'バツ' そして 'そして' 、コサイン類似度を使用します。 「x」ベクトルには値があり、 x = { 3, 2, 0, 5 } 「y」ベクトルには値があり、 y = { 1, 0, 0, 0 } コサイン類似度を計算する式は次のとおりです。 
(x, y) = x。 y / ||x|| ||そして||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3 ||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16 ||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1 ∴ (x, y) = 3 / (6.16 * 1) = 0.49>
2 つのベクトル「x」と「y」の間の非類似性は、次の式で与えられます。
∴ (x, y) = 1 - (x, y) = 1 - 0.49 = 0.51>
- 2 つのベクトル間のコサイン類似度は「θ」で測定されます。
- θ = 0°の場合、「x」ベクトルと「y」ベクトルは重なっており、これらが類似していることがわかります。
- θ = 90°の場合、「x」ベクトルと「y」ベクトルは異なります。
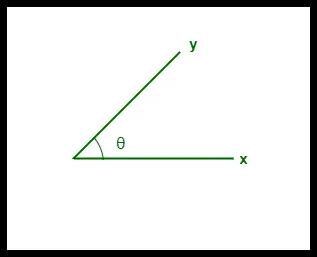
2 つのベクトル間のコサイン類似度
利点:
- コサイン類似度は、2 つの類似したデータ オブジェクトのサイズが原因でユークリッド距離だけ離れていても、それらの間の角度がさらに小さくなる可能性があるため、有益です。角度が小さいほど類似度が高くなります。
- 多次元空間にプロットすると、コサイン類似度はデータ オブジェクトの大きさではなく方向 (角度) を捉えます。