コタンジェントの公式

三角法は、直角三角形の辺の長さと角度の関係を扱う数学の重要な分野です。サイン、コサイン、タンジェント、コセカント、セカント、およびコタンジェントは、6 つの三角比または関数です。ここで、三角比は直角三角形の辺間の比として表されます。

sinθ = 反対側/斜辺
cos θ = 隣接辺/斜辺
Tanθ = 反対側/隣接側
cosec θ = 1/sin θ = 斜辺/反対側
secθ = 1/cosθ = 斜辺/隣接辺
cotθ = 1/tanθ = 隣接側/反対側

コタンジェント関数は、指定されたタンジェント関数の逆関数です。直角三角形の余接角の値は、指定された角度に隣接する辺の長さと、指定された角度の反対側の辺の長さの比です。コタンジェント関数をcotと書きます。

三角ABC

さて、角度 θ の余接公式は次のようになります。

cot θ = (隣接側)/(反対側)

コタンジェント関数は、第 1 象限と第 3 象限では正となり、第 2 象限と第 4 象限では負になります。

cot (2π + θ) = cot θ (1^セント四分円）
cot (π – θ) = – cot θ (2^nd四分円）
cot (π + θ) = cot θ (3^rd四分円）
cot (2π – θ) = – cot θ (4^番目四分円）

負の角度の余接は正の角度の余接の負の値であるため、余接関数は負の関数です。

cot (-θ) = – cot θ

正接関数に関して言えば、余接関数は次のように書かれます。

cotθ = 1/tanθ

（または）

cot θ = Tan (90° – θ) (または) Tan (π/2 – θ)

サイン関数とコサイン関数に関するコタンジェント関数は次のように記述できます。

cotθ = cosθ/sinθ

cot θ = 隣接する側/反対側であることがわかります。
Javaのリストボックス

次に、分子と分母の両方を斜辺で割ります。

⇒ cotθ = (隣辺/斜辺) / (反対側/斜辺)

sin θ = 反対側/斜辺であることがわかります。

cos θ = 隣接辺/斜辺

したがって、cot θ = cos θ/sin θ

正弦関数の観点からのコタンジェント関数は次のように書くことができます。

cot θ = (√1 – sin ² i)/罪 i

cot θ = cos θ/sin θ であることがわかっています。

私たちが持っているピタゴラス的アイデンティティから。

コス²θ+sin²θ = 1

⇒ cosθ = √1 – sin²私

したがって、cot θ = $frac{sqrt{left(1-sin^{2} heta ight)}}{sin heta}$

コサイン関数の観点からコタンジェント関数は次のように書くことができます。

cotθ = cosθ/(√1 -cos ² 私）

cot θ = cos θ/sin θ であることがわかっています。

私たちが持っているピタゴラス的アイデンティティから。

コス²θ+sin²θ = 1

sinθ = √1 – cos²私

したがって、cot θ = $frac{cos heta}{sqrt{left(1-cos^{2} heta ight)}}$

セカント関数とコセカント関数に関するコタンジェント関数は次のように記述できます。

cot θ = cosec θ/sec θ
スピーカーとは何ですか

cot θ = cos θ/sin θ となります。

これは、cot θ = (1/sin θ) / (1/cos θ) と書くことができます。

⇒ cot θ = cosec θ/sec θ

コセカント関数に関するコタンジェント関数は次のように記述できます。

cot θ = √(cosec ² - 1)

ピタゴラス的恒等式から、次のようになります。

コセック²θ – コット²θ = 1

⇒ 簡易ベッド²θ = 1 – コ秒²- 1

したがって、cot θ = √(cosec²- 1)

セカント関数の観点からコタンジェント関数は次のように記述できます。

コットθ = 1/(√秒 ² i – 1)

ピタゴラス的恒等式から、次のようになります。

秒²θ – それで²θ = 1

タンθ = √秒²私 – 1

cot θ = 1/tan θ であることがわかっています。

したがって、コットθ = $frac{1}{sqrt{left(1-sec^{2} heta ight)}}$

三角比表

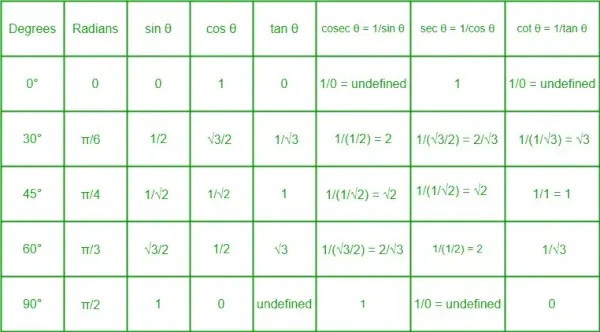
三角比表

余接の法則または余接の法則

余接の法則は正弦の法則に似ていますが、ここでは半角が関係します。余接の法則は、三角形の辺の長さと 3 つの角の半分の余接との関係を説明します。三角形 ABC について考えます。ここで、a、b、c は三角形の辺の長さです。

余接の法則は次のように述べています。

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

ここで、s は三角形 ABC の半周長、r は三角形の内接円の半径です。

s = (a + b + c)/2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

サンプル問題

問題 1:tan θ = 3/4 の場合の cot θ の値を求めます。

解決：

与えられたデータ、tan θ = 3/4

私達はことを知っています、 cotθ = 1/tanθ

⇒ コットθ = 1/(3/4) = 4/3

したがって、コットθ = 4/3

問題 2: cot α、sin α = 1/3、cos α = 2√2/3 の値を求めます。

解決：

与えられたデータ、sin α = 1/3 および cos α = 2√2/3

私達はことを知っています、 cot α = cos α/sin α

⇒ cot α = (2√2/3) / (1/3) = 2√2

したがって、cot αの値 = 2√2
文字列を追加する

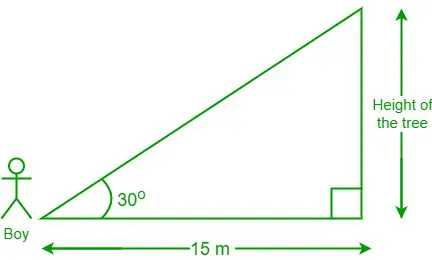
問題 3: 木から 15 メートル離れたところに立っている少年は、木のてっぺんに対して 30 度の角度を見ています。木の高さはどれくらいですか？

解決：

与えられたデータからの図

与えられたデータによると、少年と木の根元の間の距離 = 15 m、θ = 30°

木の高さを「h」とします

我々は持っています、 cot θ = 隣接側/反対側

⇒ コット 30° = 15/h

⇒ √3 = 15/h [コット 30° = √3 なので]

⇒ h = 15/√3

⇒ h = 5√3 m

したがって、木の高さ = 5√3 m

問題 4: sec x = 6/5 の場合の cot x の値を求めます。

解決：

与えられたデータ、秒 x = 6/5

我々は持っています、秒 ² × – それで ² x = 1

⇒ (6/5)²- それで²x = 1

⇒ 36/25 – それで²x = 1

⇒それで²x = 36/25 – 1

⇒それで²x = 11/25

⇒ タン x = √(11/25) = √11/5

私達はことを知っています、 コット x = 1/タン x

⇒ コット x = 1/(√11/5) = 5/√11

したがって、cot x = 5/√11

問題 5: cosec θ = 25/24 の場合の cot θ の値を求めます。

解決：

与えられたデータ、cosec θ = 25/24

私達はことを知っています、 cot θ = √(cosec ² - 1)

⇒ コットθ = √(25/24)²- 1

⇒ コットθ =√(625 – 576)/576 = √49/576

⇒ コットθ = 7/24

したがって、cot θ の値 = 7/24
xamppの代替品

問題 6: sin β = 5/13 の場合の cot β の値を求めます。

解決：

与えられたデータ、sin β = 5/13

私達はことを知っています、 それなし ² β+cos ² β = 1

⇒ (5/13)²+cos²β = 1

⇒ コス²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ cosβ = √144/169 = 12/13

cot β = cosβ/sin β

= (12/13) / (5/13)

⇒ コットβ＝12/5

したがって、cot β の値 = 12/5
javacが認識されない

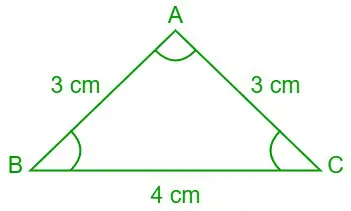
問題 7: 余接の法則を使用して、三角形 ABC の 3 辺の長さが a = 4 cm、b= 3 cm、c= の場合の∠A、∠B、∠C の値 (度単位) を求めてください。 3cm。

解決：

a = 4 cm、b = 3 cm、c = 3 cm とすると、

三角ABC

余接の法則より、

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

ここで、s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒ r = √[(1)(2)(2)/5]

三角形の半径 r = 2/√5

余接の法則の方程式より、

コット (A/2)/1 = 1/(2/√5)

⇒ コット (A/2) = √5/2 ⇒ A/2 = コット^-1(√5/2)

⇒ (A/2) = 41.8° ⇒ ∠A = 83.6°

cot(B/2)/2 = 1/(2/√5)

⇒ cot(B/2)/2 = √5/2 ⇒ cot(B/2) = √5

⇒ (B/2) = 簡易ベッド^-1(√5) = 24.1° ⇒ ∠B = 48.2°

コット (C/2)/2 = 1/(2/√5)

⇒ cot(C/2) = √5 ⇒ (C/2) = cot^-1(√5)

⇒ (C/2) = 24.1° ⇒ ∠C = 48.2°

したがって、三角形ABCの角度は∠A = 83.6°、∠B = 48.2°、∠C = 48.2°となります。