この記事では、56 ビットのキー長で知られる歴史的な暗号化アルゴリズムである Data Encryption Standard (DES) について説明します。その運用、キー変換、暗号化プロセスを調査し、データ セキュリティにおけるその役割と今日の状況における脆弱性を明らかにします。
DESとは何ですか?
データ暗号化標準 (DES) は、データ セキュリティにおいて重要な役割を果たしてきた 56 ビットのキー長を持つブロック暗号です。 。 データ暗号化標準 (DES) は非常に強力な攻撃に対して脆弱であることが判明しており、そのため DES の人気は若干低下傾向にあります。 DES はブロック暗号であり、データを次のサイズのブロックで暗号化します。 64ビット これは、64 ビットの平文が DES への入力として送られ、64 ビットの暗号文が生成されることを意味します。同じアルゴリズムとキーが暗号化に使用され、 復号化 、若干の違いはありますが。キーの長さは 56ビット 。
基本的な考え方を以下に示します。
AndroidでYouTubeの広告をブロックする方法
DES では 56 ビットのキーが使用されると述べました。実際には、初期キーは 64 ビットで構成されます。ただし、DES プロセスが開始される前に、キーの 8 ビットごとに破棄されて 56 ビットのキーが生成されます。つまり、ビット位置 8、16、24、32、40、48、56、および 64 が破棄されます。

したがって、キーの 8 ビットごとに破棄すると、 56ビット鍵 オリジナルから 64ビット鍵 。
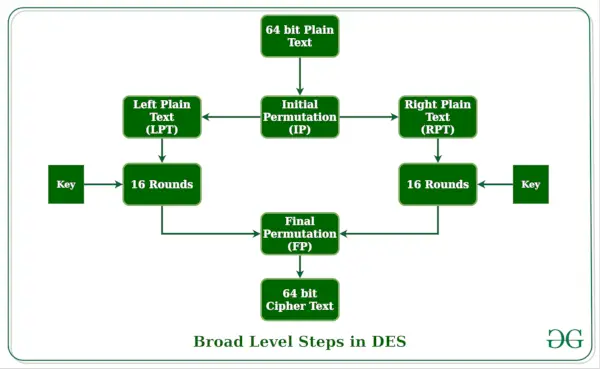
DES は、次の 2 つの基本的な属性に基づいています。 暗号化 : 置換 (混乱とも呼ばれます) と転置 (拡散とも呼ばれます)。 DES は 16 のステップで構成され、各ステップはラウンドと呼ばれます。各ラウンドでは、置換と転置のステップが実行されます。次に、DES の大まかな手順について説明します。
- 最初のステップでは、64 ビットのプレーン テキスト ブロックが最初のブロックに渡されます。 順列 (IP)機能。
- 最初の置換はプレーンテキストに対して実行されます。
- 次に、初期置換 (IP) によって、置換されたブロックの 2 つの半分が生成されます。左プレーンテキスト (LPT) と右プレーンテキスト (RPT) と言います。
- ここで、各 LPT と RPT は 16 ラウンドの暗号化プロセスを経ます。
- 最後に、LPT と RPT が再結合され、結合されたブロックに対して最終置換 (FP) が実行されます。
- このプロセスの結果、64 ビットの暗号文が生成されます。
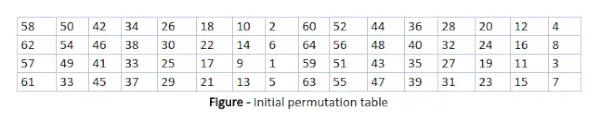
初期順列 (IP)
すでに述べたように、初期順列 (IP) は 1 回だけ発生し、最初のラウンドの前に発生します。図に示すように、IP での転置がどのように進められるべきかを示唆しています。たとえば、IP は元のプレーン テキスト ブロックの最初のビットを元のプレーン テキストの 58 番目のビットに置き換え、2 番目のビットを元のプレーン テキスト ブロックの 50 番目のビットに置き換えると述べています。
これは、元のプレーン テキスト ブロックのビット位置をごちゃ混ぜにしていることに他なりません。同じ規則が、図に示されている他のすべてのビット位置に適用されます。
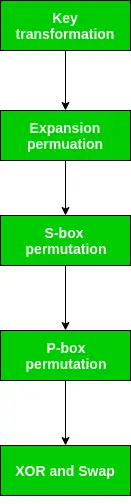
IP が完了した後に述べたように、結果として得られる 64 ビットの並べ替えられたテキスト ブロックは 2 つのハーフ ブロックに分割されます。各ハーフブロックは 32 ビットで構成され、16 ラウンドのそれぞれは、図に概説されている大まかなレベルのステップで構成されます。
ステップ 1: キー変換
初期の 64 ビット キーは、初期キーの 8 ビットごとに破棄されることで 56 ビット キーに変換されることに注目しました。したがって、それぞれに 56 ビットのキーが利用可能です。この 56 ビットのキーから、キー変換と呼ばれるプロセスを使用して、ラウンドごとに異なる 48 ビットのサブキーが生成されます。このため、56 ビットの鍵は 28 ビットずつの 2 つの半分に分割されます。これらの半分は、ラウンドに応じて 1 つまたは 2 つの位置だけ左に循環的にシフトされます。
例えば: ラウンド番号が 1、2、9、または 16 の場合、シフトは 1 つの位置だけで行われ、他のラウンドでは循環シフトが 2 つの位置で行われます。ラウンドごとにシフトされる鍵ビットの数を図に示します。

適切なシフトの後、56 ビットのうち 48 ビットが選択されます。要件に基づいて 48 ビットから 64 ビットまたは 56 ビットを取得する可能性があります。これは、このモデルが非常に多用途であり、必要または提供されるあらゆる範囲の要件を処理できることを認識するのに役立ちます。 56 ビットのうち 48 ビットを選択するためのテーブルを次の図に示します。たとえば、シフト後、ビット番号 14 は最初の位置に移動し、ビット番号 17 は 2 番目の位置に移動します。テーブルを観察すると、48 ビットの位置のみが含まれていることがわかります。ビット番号 18 は、他の 7 ビットと同様に、56 ビット キーを 48 ビット キーに減らすために破棄されます (表には見つかりません)。キー変換プロセスには置換と、元の 56 ビット キーの 48 ビット サブセットの選択が含まれるため、圧縮置換と呼ばれます。
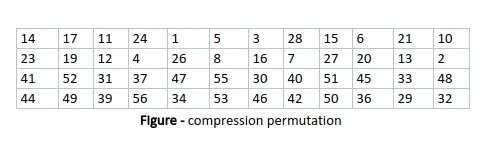
この圧縮順列技術により、各ラウンドでキー ビットの異なるサブセットが使用されます。そのため、DES をクラックするのは容易ではありません。
スクリプトを実行する方法
ステップ 2: 拡張順列
最初の並べ替えの後、Left Plain Text(LPT) と Right Plain Text(RPT) と呼ばれる 2 つの 32 ビット プレーン テキスト領域ができたことを思い出してください。拡張順列中に、RPT は 32 ビットから 48 ビットに拡張されます。ビットも並べ替えられるため、拡張並べ替えと呼ばれます。これは、32 ビット RPT が 8 つのブロックに分割され、各ブロックが 4 ビットで構成されるときに発生します。次に、前のステップの各 4 ビット ブロックが対応する 6 ビット ブロックに拡張されます。つまり、4 ビット ブロックごとにさらに 2 ビットが追加されます。
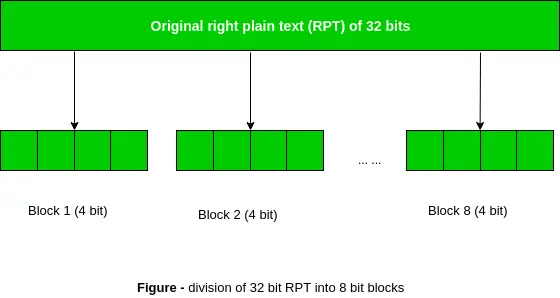
このプロセスにより、出力の作成中に入力ビットの拡張と並べ替えが行われます。キー変換プロセスでは、56 ビットのキーが 48 ビットに圧縮されます。次に、拡張置換プロセスにより、 32ビットRPT に 48ビット 。これで、48 ビット鍵は次のようになります。 無料 48 ビット RPT を使用し、その結果の出力が次のステップに渡されます。 S-ボックス置換 。
パイソン
Javaで文字列を整数に変換する
# Python3 code for the above approach> # Hexadecimal to binary conversion> def> hex2bin(s):> >mp>=> {>'0'>:>'0000'>,> >'1'>:>'0001'>,> >'2'>:>'0010'>,> >'3'>:>'0011'>,> >'4'>:>'0100'>,> >'5'>:>'0101'>,> >'6'>:>'0110'>,> >'7'>:>'0111'>,> >'8'>:>'1000'>,> >'9'>:>'1001'>,> >'A'>:>'1010'>,> >'B'>:>'1011'>,> >'C'>:>'1100'>,> >'D'>:>'1101'>,> >'E'>:>'1110'>,> >'F'>:>'1111'>}> >bin> => ''> >for> i>in> range>(>len>(s)):> >bin> => bin> +> mp[s[i]]> >return> bin> # Binary to hexadecimal conversion> def> bin2hex(s):> >mp>=> {>'0000'>:>'0'>,> >'0001'>:>'1'>,> >'0010'>:>'2'>,> >'0011'>:>'3'>,> >'0100'>:>'4'>,> >'0101'>:>'5'>,> >'0110'>:>'6'>,> >'0111'>:>'7'>,> >'1000'>:>'8'>,> >'1001'>:>'9'>,> >'1010'>:>'A'>,> >'1011'>:>'B'>,> >'1100'>:>'C'>,> >'1101'>:>'D'>,> >'1110'>:>'E'>,> >'1111'>:>'F'>}> >hex> => ''> >for> i>in> range>(>0>,>len>(s),>4>):> >ch>=> ''> >ch>=> ch>+> s[i]> >ch>=> ch>+> s[i>+> 1>]> >ch>=> ch>+> s[i>+> 2>]> >ch>=> ch>+> s[i>+> 3>]> >hex> => hex> +> mp[ch]> >return> hex> # Binary to decimal conversion> def> bin2dec(binary):> >binary1>=> binary> >decimal, i, n>=> 0>,>0>,>0> >while>(binary !>=> 0>):> >dec>=> binary>%> 10> >decimal>=> decimal>+> dec>*> pow>(>2>, i)> >binary>=> binary>/>/>10> >i>+>=> 1> >return> decimal> # Decimal to binary conversion> def> dec2bin(num):> >res>=> bin>(num).replace(>'0b'>, '')> >if>(>len>(res)>%> 4> !>=> 0>):> >div>=> len>(res)>/> 4> >div>=> int>(div)> >counter>=> (>4> *> (div>+> 1>))>-> len>(res)> >for> i>in> range>(>0>, counter):> >res>=> '0'> +> res> >return> res> # Permute function to rearrange the bits> def> permute(k, arr, n):> >permutation>=> ''> >for> i>in> range>(>0>, n):> >permutation>=> permutation>+> k[arr[i]>-> 1>]> >return> permutation> # shifting the bits towards left by nth shifts> def> shift_left(k, nth_shifts):> >s>=> ''> >for> i>in> range>(nth_shifts):> >for> j>in> range>(>1>,>len>(k)):> >s>=> s>+> k[j]> >s>=> s>+> k[>0>]> >k>=> s> >s>=> ''> >return> k> # calculating xow of two strings of binary number a and b> def> xor(a, b):> >ans>=> ''> >for> i>in> range>(>len>(a)):> >if> a[i]>=>=> b[i]:> >ans>=> ans>+> '0'> >else>:> >ans>=> ans>+> '1'> >return> ans> # Table of Position of 64 bits at initial level: Initial Permutation Table> initial_perm>=> [>58>,>50>,>42>,>34>,>26>,>18>,>10>,>2>,> >60>,>52>,>44>,>36>,>28>,>20>,>12>,>4>,> >62>,>54>,>46>,>38>,>30>,>22>,>14>,>6>,> >64>,>56>,>48>,>40>,>32>,>24>,>16>,>8>,> >57>,>49>,>41>,>33>,>25>,>17>,>9>,>1>,> >59>,>51>,>43>,>35>,>27>,>19>,>11>,>3>,> >61>,>53>,>45>,>37>,>29>,>21>,>13>,>5>,> >63>,>55>,>47>,>39>,>31>,>23>,>15>,>7>]> # Expansion D-box Table> exp_d>=> [>32>,>1>,>2>,>3>,>4>,>5>,>4>,>5>,> >6>,>7>,>8>,>9>,>8>,>9>,>10>,>11>,> >12>,>13>,>12>,>13>,>14>,>15>,>16>,>17>,> >16>,>17>,>18>,>19>,>20>,>21>,>20>,>21>,> >22>,>23>,>24>,>25>,>24>,>25>,>26>,>27>,> >28>,>29>,>28>,>29>,>30>,>31>,>32>,>1>]> # Straight Permutation Table> per>=> [>16>,>7>,>20>,>21>,> >29>,>12>,>28>,>17>,> >1>,>15>,>23>,>26>,> >5>,>18>,>31>,>10>,> >2>,>8>,>24>,>14>,> >32>,>27>,>3>,>9>,> >19>,>13>,>30>,>6>,> >22>,>11>,>4>,>25>]> # S-box Table> sbox>=> [[[>14>,>4>,>13>,>1>,>2>,>15>,>11>,>8>,>3>,>10>,>6>,>12>,>5>,>9>,>0>,>7>],> >[>0>,>15>,>7>,>4>,>14>,>2>,>13>,>1>,>10>,>6>,>12>,>11>,>9>,>5>,>3>,>8>],> >[>4>,>1>,>14>,>8>,>13>,>6>,>2>,>11>,>15>,>12>,>9>,>7>,>3>,>10>,>5>,>0>],> >[>15>,>12>,>8>,>2>,>4>,>9>,>1>,>7>,>5>,>11>,>3>,>14>,>10>,>0>,>6>,>13>]],> >[[>15>,>1>,>8>,>14>,>6>,>11>,>3>,>4>,>9>,>7>,>2>,>13>,>12>,>0>,>5>,>10>],> >[>3>,>13>,>4>,>7>,>15>,>2>,>8>,>14>,>12>,>0>,>1>,>10>,>6>,>9>,>11>,>5>],> >[>0>,>14>,>7>,>11>,>10>,>4>,>13>,>1>,>5>,>8>,>12>,>6>,>9>,>3>,>2>,>15>],> >[>13>,>8>,>10>,>1>,>3>,>15>,>4>,>2>,>11>,>6>,>7>,>12>,>0>,>5>,>14>,>9>]],> >[[>10>,>0>,>9>,>14>,>6>,>3>,>15>,>5>,>1>,>13>,>12>,>7>,>11>,>4>,>2>,>8>],> >[>13>,>7>,>0>,>9>,>3>,>4>,>6>,>10>,>2>,>8>,>5>,>14>,>12>,>11>,>15>,>1>],> >[>13>,>6>,>4>,>9>,>8>,>15>,>3>,>0>,>11>,>1>,>2>,>12>,>5>,>10>,>14>,>7>],> >[>1>,>10>,>13>,>0>,>6>,>9>,>8>,>7>,>4>,>15>,>14>,>3>,>11>,>5>,>2>,>12>]],> >[[>7>,>13>,>14>,>3>,>0>,>6>,>9>,>10>,>1>,>2>,>8>,>5>,>11>,>12>,>4>,>15>],> >[>13>,>8>,>11>,>5>,>6>,>15>,>0>,>3>,>4>,>7>,>2>,>12>,>1>,>10>,>14>,>9>],> >[>10>,>6>,>9>,>0>,>12>,>11>,>7>,>13>,>15>,>1>,>3>,>14>,>5>,>2>,>8>,>4>],> >[>3>,>15>,>0>,>6>,>10>,>1>,>13>,>8>,>9>,>4>,>5>,>11>,>12>,>7>,>2>,>14>]],> >[[>2>,>12>,>4>,>1>,>7>,>10>,>11>,>6>,>8>,>5>,>3>,>15>,>13>,>0>,>14>,>9>],> >[>14>,>11>,>2>,>12>,>4>,>7>,>13>,>1>,>5>,>0>,>15>,>10>,>3>,>9>,>8>,>6>],> >[>4>,>2>,>1>,>11>,>10>,>13>,>7>,>8>,>15>,>9>,>12>,>5>,>6>,>3>,>0>,>14>],> >[>11>,>8>,>12>,>7>,>1>,>14>,>2>,>13>,>6>,>15>,>0>,>9>,>10>,>4>,>5>,>3>]],> >[[>12>,>1>,>10>,>15>,>9>,>2>,>6>,>8>,>0>,>13>,>3>,>4>,>14>,>7>,>5>,>11>],> >[>10>,>15>,>4>,>2>,>7>,>12>,>9>,>5>,>6>,>1>,>13>,>14>,>0>,>11>,>3>,>8>],> >[>9>,>14>,>15>,>5>,>2>,>8>,>12>,>3>,>7>,>0>,>4>,>10>,>1>,>13>,>11>,>6>],> >[>4>,>3>,>2>,>12>,>9>,>5>,>15>,>10>,>11>,>14>,>1>,>7>,>6>,>0>,>8>,>13>]],> >[[>4>,>11>,>2>,>14>,>15>,>0>,>8>,>13>,>3>,>12>,>9>,>7>,>5>,>10>,>6>,>1>],> >[>13>,>0>,>11>,>7>,>4>,>9>,>1>,>10>,>14>,>3>,>5>,>12>,>2>,>15>,>8>,>6>],> >[>1>,>4>,>11>,>13>,>12>,>3>,>7>,>14>,>10>,>15>,>6>,>8>,>0>,>5>,>9>,>2>],> >[>6>,>11>,>13>,>8>,>1>,>4>,>10>,>7>,>9>,>5>,>0>,>15>,>14>,>2>,>3>,>12>]],> >[[>13>,>2>,>8>,>4>,>6>,>15>,>11>,>1>,>10>,>9>,>3>,>14>,>5>,>0>,>12>,>7>],> >[>1>,>15>,>13>,>8>,>10>,>3>,>7>,>4>,>12>,>5>,>6>,>11>,>0>,>14>,>9>,>2>],> >[>7>,>11>,>4>,>1>,>9>,>12>,>14>,>2>,>0>,>6>,>10>,>13>,>15>,>3>,>5>,>8>],> >[>2>,>1>,>14>,>7>,>4>,>10>,>8>,>13>,>15>,>12>,>9>,>0>,>3>,>5>,>6>,>11>]]]> # Final Permutation Table> final_perm>=> [>40>,>8>,>48>,>16>,>56>,>24>,>64>,>32>,> >39>,>7>,>47>,>15>,>55>,>23>,>63>,>31>,> >38>,>6>,>46>,>14>,>54>,>22>,>62>,>30>,> >37>,>5>,>45>,>13>,>53>,>21>,>61>,>29>,> >36>,>4>,>44>,>12>,>52>,>20>,>60>,>28>,> >35>,>3>,>43>,>11>,>51>,>19>,>59>,>27>,> >34>,>2>,>42>,>10>,>50>,>18>,>58>,>26>,> >33>,>1>,>41>,>9>,>49>,>17>,>57>,>25>]> def> encrypt(pt, rkb, rk):> >pt>=> hex2bin(pt)> ># Initial Permutation> >pt>=> permute(pt, initial_perm,>64>)> >print>(>'After initial permutation'>, bin2hex(pt))> ># Splitting> >left>=> pt[>0>:>32>]> >right>=> pt[>32>:>64>]> >for> i>in> range>(>0>,>16>):> ># Expansion D-box: Expanding the 32 bits data into 48 bits> >right_expanded>=> permute(right, exp_d,>48>)> ># XOR RoundKey[i] and right_expanded> >xor_x>=> xor(right_expanded, rkb[i])> ># S-boxex: substituting the value from s-box table by calculating row and column> >sbox_str>=> ''> >for> j>in> range>(>0>,>8>):> >row>=> bin2dec(>int>(xor_x[j>*> 6>]>+> xor_x[j>*> 6> +> 5>]))> >col>=> bin2dec(> >int>(xor_x[j>*> 6> +> 1>]>+> xor_x[j>*> 6> +> 2>]>+> xor_x[j>*> 6> +> 3>]>+> xor_x[j>*> 6> +> 4>]))> >val>=> sbox[j][row][col]> >sbox_str>=> sbox_str>+> dec2bin(val)> ># Straight D-box: After substituting rearranging the bits> >sbox_str>=> permute(sbox_str, per,>32>)> ># XOR left and sbox_str> >result>=> xor(left, sbox_str)> >left>=> result> ># Swapper> >if>(i !>=> 15>):> >left, right>=> right, left> >print>(>'Round '>, i>+> 1>,>' '>, bin2hex(left),> >' '>, bin2hex(right),>' '>, rk[i])> ># Combination> >combine>=> left>+> right> ># Final permutation: final rearranging of bits to get cipher text> >cipher_text>=> permute(combine, final_perm,>64>)> >return> cipher_text> pt>=> '123456ABCD132536'> key>=> 'AABB09182736CCDD'> # Key generation> # --hex to binary> key>=> hex2bin(key)> # --parity bit drop table> keyp>=> [>57>,>49>,>41>,>33>,>25>,>17>,>9>,> >1>,>58>,>50>,>42>,>34>,>26>,>18>,> >10>,>2>,>59>,>51>,>43>,>35>,>27>,> >19>,>11>,>3>,>60>,>52>,>44>,>36>,> >63>,>55>,>47>,>39>,>31>,>23>,>15>,> >7>,>62>,>54>,>46>,>38>,>30>,>22>,> >14>,>6>,>61>,>53>,>45>,>37>,>29>,> >21>,>13>,>5>,>28>,>20>,>12>,>4>]> # getting 56 bit key from 64 bit using the parity bits> key>=> permute(key, keyp,>56>)> # Number of bit shifts> shift_table>=> [>1>,>1>,>2>,>2>,> >2>,>2>,>2>,>2>,> >1>,>2>,>2>,>2>,> >2>,>2>,>2>,>1>]> # Key- Compression Table : Compression of key from 56 bits to 48 bits> key_comp>=> [>14>,>17>,>11>,>24>,>1>,>5>,> >3>,>28>,>15>,>6>,>21>,>10>,> >23>,>19>,>12>,>4>,>26>,>8>,> >16>,>7>,>27>,>20>,>13>,>2>,> >41>,>52>,>31>,>37>,>47>,>55>,> >30>,>40>,>51>,>45>,>33>,>48>,> >44>,>49>,>39>,>56>,>34>,>53>,> >46>,>42>,>50>,>36>,>29>,>32>]> # Splitting> left>=> key[>0>:>28>]># rkb for RoundKeys in binary> right>=> key[>28>:>56>]># rk for RoundKeys in hexadecimal> rkb>=> []> rk>=> []> for> i>in> range>(>0>,>16>):> ># Shifting the bits by nth shifts by checking from shift table> >left>=> shift_left(left, shift_table[i])> >right>=> shift_left(right, shift_table[i])> ># Combination of left and right string> >combine_str>=> left>+> right> ># Compression of key from 56 to 48 bits> >round_key>=> permute(combine_str, key_comp,>48>)> >rkb.append(round_key)> >rk.append(bin2hex(round_key))> print>(>'Encryption'>)> cipher_text>=> bin2hex(encrypt(pt, rkb, rk))> print>(>'Cipher Text : '>, cipher_text)> print>(>'Decryption'>)> rkb_rev>=> rkb[::>->1>]> rk_rev>=> rk[::>->1>]> text>=> bin2hex(encrypt(cipher_text, rkb_rev, rk_rev))> print>(>'Plain Text : '>, text)> # This code is contributed by Aditya Jain> |
>
結合を使用してSQLで更新する
>
JavaScript
// Define DES key and plaintext> const key =>'0123456789abcdef'>;> const plaintext =>'Hello, world!'>;> // Perform DES encryption> const des =>new> DES(key);> const ciphertext = des.encrypt(plaintext);> // Perform DES decryption> const decrypted = des.decrypt(ciphertext);> // Print results> console.log(>'Plaintext: '>, plaintext);> console.log(>'Ciphertext: '>, ciphertext);> console.log(>'Decrypted: '>, decrypted);> // Define DES class> class DES {> >constructor(key) {> >// Initialize DES with key> >this>.key = CryptoJS.enc.Hex.parse(key);> >}> >encrypt(plaintext) {> >// Perform DES encryption on plaintext> >const encrypted = CryptoJS.DES.encrypt(> >plaintext,> >this>.key,> >{ mode: CryptoJS.mode.ECB }> >);> >// Return ciphertext as hex string> >return> encrypted.ciphertext.toString();> >}> >decrypt(ciphertext) {> >// Parse ciphertext from hex string> >const ciphertextHex = CryptoJS.enc.Hex.parse(ciphertext);> >// Perform DES decryption on ciphertext> >const decrypted = CryptoJS.DES.decrypt(> >{ ciphertext: ciphertextHex },> >this>.key,> >{ mode: CryptoJS.mode.ECB }> >);> >// Return decrypted plaintext as UTF-8 string> >return> decrypted.toString(CryptoJS.enc.Utf8);> >}> }> |
>
>出力
...60AF7CA5 Round 12 FF3C485F 22A5963B C2C1E96A4BF3 Round 13 22A5963B 387CCDAA 99C31397C91F Round 14 387CCDAA BD2DD2AB 251B8BC717D0 Round 15 BD2DD2AB CF26B472 3330C5D9A36D Round 16 19BA9212 CF26B472 181C5D75C66D Cipher Text: C0B7A8D05F3A829C Decryption After initial permutation: 19BA9212CF26B472 After splitting: L0=19BA9212 R0=CF26B472 Round 1 CF26B472 BD2DD2AB 181C5D75C66D Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D Round 3 387CCDAA 22A5963B 251B8BC717D0 Round 4 22A5963B FF3C485F 99C31397C91F Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3 Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5 Round 7 10AF9D37 308BEE97 02765708B5BF Round 8 308BEE97 A9FC20A3 84BB4473DCCC Round 9 A9FC20A3 2E8F9C65 34F822F0C66D Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0 Round 11 A15A4B87 236779C2 C1948E87475E Round 12 236779C2 B8089591 69A629FEC913 Round 13 B8089591 4A1210F6 DA2D032B6EE3 Round 14 4A1210F6 5A78E394 06EDA4ACF5B5 Round 15 5A78E394 18CA18AD 4568581ABCCE Round 16 14A7D678 18CA18AD 194CD072DE8C Plain Text: 123456ABCD132536>
出力:
Encryption: After initial permutation: 14A7D67818CA18AD After splitting: L0=14A7D678 R0=18CA18AD Round 1 18CA18AD 5A78E394 194CD072DE8C Round 2 5A78E394 4A1210F6 4568581ABCCE Round 3 4A1210F6 B8089591 06EDA4ACF5B5 Round 4 B8089591 236779C2 DA2D032B6EE3 Round 5 236779C2 A15A4B87 69A629FEC913 Round 6 A15A4B87 2E8F9C65 C1948E87475E Round 7 2E8F9C65 A9FC20A3 708AD2DDB3C0 Round 8 A9FC20A3 308BEE97 34F822F0C66D Round 9 308BEE97 10AF9D37 84BB4473DCCC Round 10 10AF9D37 6CA6CB20 02765708B5BF Round 11 6CA6CB20 FF3C485F 6D5560AF7CA5 Round 12 FF3C485F 22A5963B C2C1E96A4BF3 Round 13 22A5963B 387CCDAA 99C31397C91F Round 14 387CCDAA BD2DD2AB 251B8BC717D0 Round 15 BD2DD2AB CF26B472 3330C5D9A36D Round 16 19BA9212 CF26B472 181C5D75C66D Cipher Text: C0B7A8D05F3A829C Decryption After initial permutation: 19BA9212CF26B472 After splitting: L0=19BA9212 R0=CF26B472 Round 1 CF26B472 BD2DD2AB 181C5D75C66D Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D Round 3 387CCDAA 22A5963B 251B8BC717D0 Round 4 22A5963B FF3C485F 99C31397C91F Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3 Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5 Round 7 10AF9D37 308BEE97 02765708B5BF Round 8 308BEE97 A9FC20A3 84BB4473DCCC Round 9 A9FC20A3 2E8F9C65 34F822F0C66D Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0 Round 11 A15A4B87 236779C2 C1948E87475E Round 12 236779C2 B8089591 69A629FEC913 Round 13 B8089591 4A1210F6 DA2D032B6EE3 Round 14 4A1210F6 5A78E394 06EDA4ACF5B5 Round 15 5A78E394 18CA18AD 4568581ABCCE Round 16 14A7D678 18CA18AD 194CD072DE8C Plain Text: 123456ABCD132536>
結論
結論として、データ暗号化標準 (DES) は ブロック暗号 56 ビットのキー長を備えており、データ セキュリティにおいて重要な役割を果たしています。しかし、脆弱性のため、その人気は低下しました。 DES は、鍵変換、拡張順列、置換を含む一連のラウンドを通じて動作し、最終的に平文から暗号文を生成します。 DES には歴史的な重要性がありますが、より安全性を考慮することが重要です 暗号化 現代のデータ保護ニーズに応える代替手段。
よくある質問
Q.1 : データ暗号化のための DES の代替として何を考慮する必要がありますか?
答え:
最新のデータ暗号化のニーズに対応するには、次のような強力な暗号化アルゴリズムの使用を検討してください。 AES (高度な暗号化標準)。
Java配列ソート
Q.2 : DES ではラウンドごとに 48 ビットのサブキーがどのように生成されますか?
答え:
DES の各ラウンドの 48 ビットのサブキーは、循環シフトと置換のプロセスを通じて 56 ビットのキーから導出され、キーの多様性を確保します。

