削除関数は、二分探索木から指定したノードを削除するために使用されます。ただし、二分探索木の性質に違反しない方法で二分探索木からノードを削除する必要があります。二分探索木からノードを削除する状況は 3 つあります。
削除するノードはリーフノードです
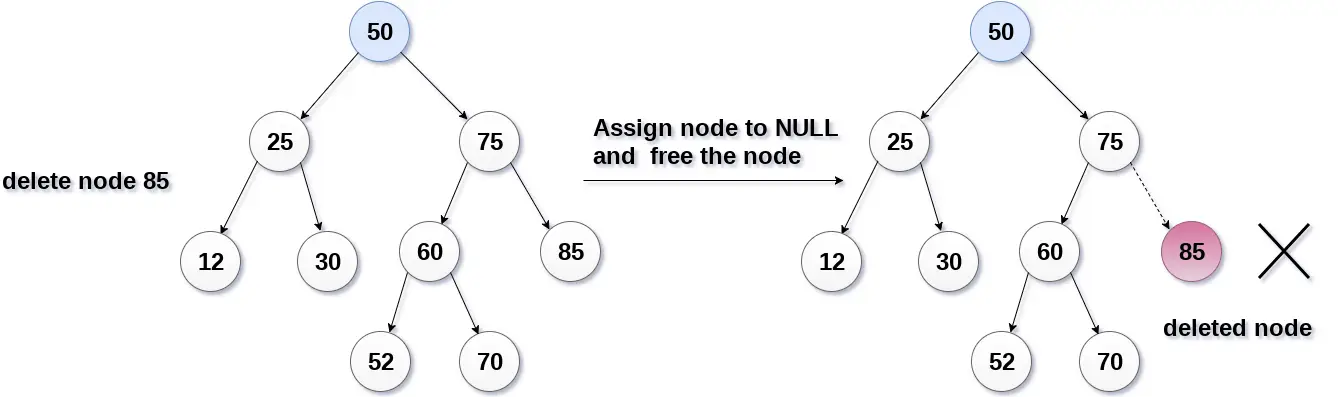
これは最も単純なケースです。この場合、リーフ ノードを NULL に置き換え、割り当てられたスペースを単純に解放します。
次の図では、ノード 85 を削除しています。このノードはリーフ ノードであるため、ノードは NULL に置き換えられ、割り当てられたスペースが解放されます。
削除するノードには子が 1 つだけあります。
この場合、ノードをその子ノードに置き換えて、削除する値が含まれる子ノードを削除します。これを NULL に置き換えて、割り当てられたスペースを解放するだけです。
次の図では、ノード 12 が削除されます。子供は一人だけです。ノードはその子ノードに置き換えられ、置き換えられたノード 12 (現在はリーフ ノード) は単純に削除されます。

削除するノードには 2 つの子があります。
他の 2 つのケースに比べて少し複雑なケースです。ただし、削除されるノードは、(削除される) ノード値がツリーの葉に配置されるまで、再帰的にその順序の後続ノードまたは先行ノードに置き換えられます。この手順の後、ノードを NULL に置き換え、割り当てられた領域を解放します。
次の図では、ツリーのルート ノードであるノード 50 が削除されます。以下に示すツリーの順序どおりの走査。
6、25、30、50、52、60、70、75。
50 をその順序で後続する 52 に置き換えます。ここで、50 はツリーの葉に移動され、単純に削除されます。

アルゴリズム
削除(ツリー、アイテム)
「ツリー内にアイテムが見つかりません」と書き込みます ELSE IF ITEM DATA
削除(TREE->LEFT, ITEM)
ELSE IF アイテム > ツリー -> データ
削除(ツリー -> 右、アイテム)
ELSE IF ツリー -> 左かつツリー -> 右
SET TEMP = findLargestNode(TREE -> LEFT)
ツリーの設定 -> データ = 温度 -> データ
削除(ツリー -> 左、温度 -> データ)
それ以外
設定温度 = 木
ツリー -> 左 = NULL かつツリー -> 右 = NULL の場合
ツリーを設定 = NULL
ELSE IF TREE -> LEFT != NULL
ツリーを設定 = ツリー -> 左
それ以外
ツリー = ツリー -> 右に設定
[IFの終わり]
フリーテンポ
[IFの終わり]
関数:
void deletion(Node*& root, int item) { Node* parent = NULL; Node* cur = root; search(cur, item, parent); if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur- >right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? Cur- >left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } Node* findMinimum(Node* cur) { while(cur->left != NULL) { cur = cur->left; } return cur; } 