あ ハッシュ表 データの素早い挿入、削除、取得を可能にするデータ構造です。これは、ハッシュ関数を使用してキーを配列内のインデックスにマップすることで機能します。この記事では、衝突を処理するために別個のチェーンを使用して Python でハッシュ テーブルを実装します。
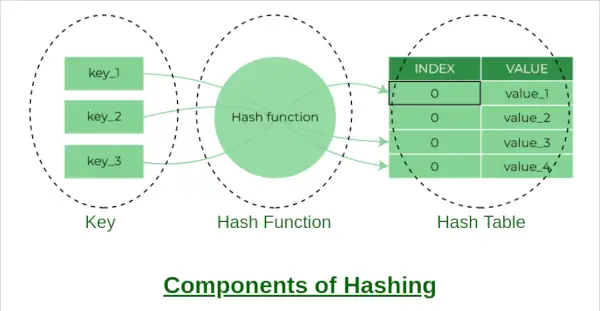
ハッシュの構成要素
個別のチェーンは、ハッシュ テーブル内の衝突を処理するために使用される手法です。 2 つ以上のキーが配列内の同じインデックスにマップされる場合、それらはそのインデックスのリンク リストに格納されます。これにより、複数の値を同じインデックスに保存し、キーを使用してそれらの値を取得できるようになります。
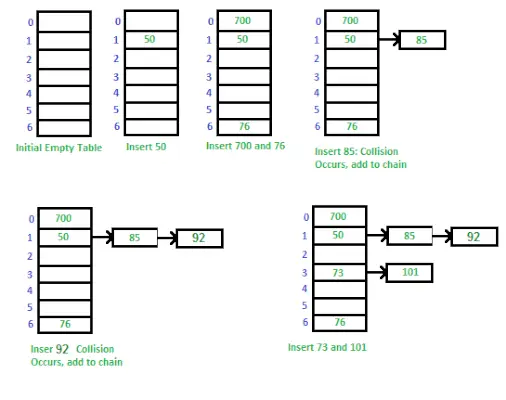
セパレートチェーンを使用したハッシュテーブルの実装方法
個別のチェーンを使用してハッシュ テーブルを実装する方法:
2 つのクラスを作成します。 ノード ' そして ' ハッシュ表 '。
「 ノード ' クラスはリンクされたリスト内のノードを表します。各ノードには、キーと値のペアに加えて、リスト内の次のノードへのポインターが含まれます。
Python3
class> Node:> >def> __init__(>self>, key, value):> >self>.key>=> key> >self>.value>=> value> >self>.>next> => None> |
>
>
「HashTable」クラスには、リンクされたリストを保持する配列と、ハッシュ テーブルからデータを挿入、取得、削除するメソッドが含まれます。
Python3
class> HashTable:> >def> __init__(>self>, capacity):> >self>.capacity>=> capacity> >self>.size>=> 0> >self>.table>=> [>None>]>*> capacity> |
>
>
「 __熱い__ ' メソッドは、指定された容量でハッシュ テーブルを初期化します。 「」を設定します 容量 ' そして ' サイズ ' 変数を使用し、配列を「なし」に初期化します。
次の方法は「 _ハッシュ ' 方法。このメソッドはキーを受け取り、キーと値のペアを格納する配列内のインデックスを返します。 Python の組み込みハッシュ関数を使用してキーをハッシュし、モジュロ演算子を使用して配列内のインデックスを取得します。
Python3
def> _hash(>self>, key):> >return> hash>(key)>%> self>.capacity> |
>
>
の '入れる' メソッドは、キーと値のペアをハッシュ テーブルに挿入します。 ‘を使用してペアを保存するインデックスを取得します。 _ハッシュ ' 方法。そのインデックスにリンクされたリストがない場合は、キーと値のペアを持つ新しいノードを作成し、それをリストの先頭に設定します。そのインデックスにリンクされたリストがある場合は、最後のノードが見つかるかキーがすでに存在するまでリストを繰り返し、キーがすでに存在する場合は値を更新します。キーが見つかった場合は、値を更新します。キーが見つからない場合は、新しいノードを作成し、リストの先頭に追加します。
Python3
def> insert(>self>, key, value):> >index>=> self>._hash(key)> >if> self>.table[index]>is> None>:> >self>.table[index]>=> Node(key, value)> >self>.size>+>=> 1> >else>:> >current>=> self>.table[index]> >while> current:> >if> current.key>=>=> key:> >current.value>=> value> >return> >current>=> current.>next> >new_node>=> Node(key, value)> >new_node.>next> => self>.table[index]> >self>.table[index]>=> new_node> >self>.size>+>=> 1> |
>
>
の 検索 メソッドは、指定されたキーに関連付けられた値を取得します。まず、キーと値のペアを保存するインデックスを取得します。 _ハッシュ 方法。次に、そのインデックスにあるリンク リストでキーを検索します。キーが見つかった場合は、関連付けられた値を返します。キーが見つからない場合は、 キーエラー 。
Python3
def> search(>self>, key):> >index>=> self>._hash(key)> >current>=> self>.table[index]> >while> current:> >if> current.key>=>=> key:> >return> current.value> >current>=> current.>next> >raise> KeyError(key)> |
>
>
の '取り除く' メソッドは、ハッシュ テーブルからキーと値のペアを削除します。まず、` を使用してペアを保存するインデックスを取得します。 _ハッシュ `メソッド。次に、そのインデックスにあるリンク リストでキーを検索します。キーが見つかった場合は、リストからノードを削除します。キーが見つからない場合は、「`」が発生します。 キーエラー `。
Python3
def> remove(>self>, key):> >index>=> self>._hash(key)> > >previous>=> None> >current>=> self>.table[index]> > >while> current:> >if> current.key>=>=> key:> >if> previous:> >previous.>next> => current.>next> >else>:> >self>.table[index]>=> current.>next> >self>.size>->=> 1> >return> >previous>=> current> >current>=> current.>next> > >raise> KeyError(key)> |
>
>
「__str__」 ハッシュ テーブルの文字列表現を返すメソッド。
Python3
部分文字列文字列java
def> __str__(>self>):> >elements>=> []> >for> i>in> range>(>self>.capacity):> >current>=> self>.table[i]> >while> current:> >elements.append((current.key, current.value))> >current>=> current.>next> >return> str>(elements)> |
>
>
「HashTable」クラスの完全な実装は次のとおりです。
Python3
class> Node:> >def> __init__(>self>, key, value):> >self>.key>=> key> >self>.value>=> value> >self>.>next> => None> > > class> HashTable:> >def> __init__(>self>, capacity):> >self>.capacity>=> capacity> >self>.size>=> 0> >self>.table>=> [>None>]>*> capacity> > >def> _hash(>self>, key):> >return> hash>(key)>%> self>.capacity> > >def> insert(>self>, key, value):> >index>=> self>._hash(key)> > >if> self>.table[index]>is> None>:> >self>.table[index]>=> Node(key, value)> >self>.size>+>=> 1> >else>:> >current>=> self>.table[index]> >while> current:> >if> current.key>=>=> key:> >current.value>=> value> >return> >current>=> current.>next> >new_node>=> Node(key, value)> >new_node.>next> => self>.table[index]> >self>.table[index]>=> new_node> >self>.size>+>=> 1> > >def> search(>self>, key):> >index>=> self>._hash(key)> > >current>=> self>.table[index]> >while> current:> >if> current.key>=>=> key:> >return> current.value> >current>=> current.>next> > >raise> KeyError(key)> > >def> remove(>self>, key):> >index>=> self>._hash(key)> > >previous>=> None> >current>=> self>.table[index]> > >while> current:> >if> current.key>=>=> key:> >if> previous:> >previous.>next> => current.>next> >else>:> >self>.table[index]>=> current.>next> >self>.size>->=> 1> >return> >previous>=> current> >current>=> current.>next> > >raise> KeyError(key)> > >def> __len__(>self>):> >return> self>.size> > >def> __contains__(>self>, key):> >try>:> >self>.search(key)> >return> True> >except> KeyError:> >return> False> > > # Driver code> if> __name__>=>=> '__main__'>:> > ># Create a hash table with> ># a capacity of 5> >ht>=> HashTable(>5>)> > ># Add some key-value pairs> ># to the hash table> >ht.insert(>'apple'>,>3>)> >ht.insert(>'banana'>,>2>)> >ht.insert(>'cherry'>,>5>)> > ># Check if the hash table> ># contains a key> >print>(>'apple'> in> ht)># True> >print>(>'durian'> in> ht)># False> > ># Get the value for a key> >print>(ht.search(>'banana'>))># 2> > ># Update the value for a key> >ht.insert(>'banana'>,>4>)> >print>(ht.search(>'banana'>))># 4> > >ht.remove(>'apple'>)> ># Check the size of the hash table> >print>(>len>(ht))># 3> |
>
>出力
True False 2 4 3>
時間の複雑さと空間の複雑さ:
- の 時間の複雑さ の 入れる 、 検索 そして 取り除く 個別のチェーンを使用するハッシュ テーブル内のメソッドは、ハッシュ テーブルのサイズ、ハッシュ テーブル内のキーと値のペアの数、および各インデックスでのリンク リストの長さに依存します。
- 適切なハッシュ関数とキーの均一な分散を仮定すると、これらのメソッドの予想時間計算量は次のようになります。 ○(1) 操作ごとに。ただし、最悪の場合、時間計算量が大幅に増加する可能性があります。 の上) ここで、n はハッシュ テーブル内のキーと値のペアの数です。
- ただし、衝突の可能性を最小限に抑え、良好なパフォーマンスを確保するには、適切なハッシュ関数とハッシュ テーブルの適切なサイズを選択することが重要です。
- の 空間の複雑さ 個別のチェーンを使用したハッシュ テーブルのサイズは、ハッシュ テーブルのサイズと、ハッシュ テーブルに格納されているキーと値のペアの数によって異なります。
- ハッシュテーブル自体は オ(メートル) space、m はハッシュ テーブルの容量です。各リンク リスト ノードは、 ○(1) スペースが必要であり、リンク リストには最大で n 個のノードを含めることができます。ここで、n はハッシュ テーブルに格納されているキーと値のペアの数です。
- したがって、空間の総複雑さは次のようになります。 O(m + n) 。
結論:
実際には、スペースの使用量と衝突の可能性のバランスをとるために、ハッシュ テーブルの適切な容量を選択することが重要です。容量が小さすぎると衝突の可能性が高まり、パフォーマンスが低下する可能性があります。一方、容量が大きすぎると、ハッシュ テーブルが必要以上にメモリを消費する可能性があります。
