三角形の内心 は、三角形の 3 つの角の二等分線すべての交点です。内心は、三角形の角を半分に切った線が集まる重要な点です。この点は、三角形の内側に完全に収まり、3 つの辺すべてに同じに接する内接円と呼ばれる円の中心でもあります。この記事では、この点が重要な理由、コンパスや数字を使用してそれを見つける方法、円の内心の特性など、三角形の内心のさまざまな概念について説明します。
目次
ユーザーのmysqlを表示
三角形の内心とは何ですか?
三角形の内心は、名前が示すように、三角形の中心点です。内心と呼ばれるこの点は、内角を二等分するすべての線が交わる交差点に形成されます。三角形の 3 辺すべてからの点の距離は同じです。三角形の内接円は三角形の内側に完全な円も収まり、この円は三角形の内接円と呼ばれます。
内心の定義
三角形の内心は、三角形の内角を半分に切る 3 本の線がすべて集まる点です。この点は三角形の 3 つの辺から同じ距離にあり、三角形の中心のようになります。これは、内接円と呼ばれる、三角形の内側にぴったり収まる最大の円の中心でもあります。内中心を記号化するには、通常、文字 I を使用します。
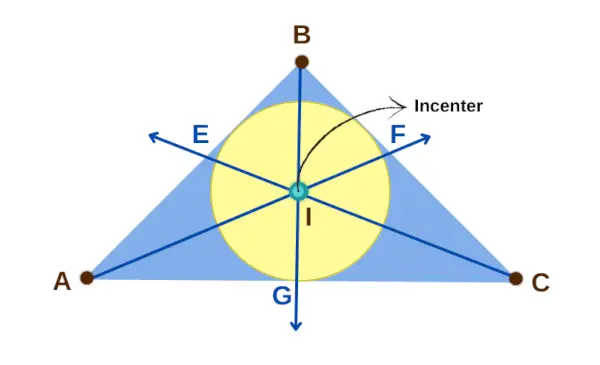
三角形の内心
三角形の内心の性質
三角形の内心のいくつかの重要な特性を以下に示します。
プロパティ 1: もし 私 が三角形 ABC の内心である場合、3 組の線分、AE と AG、CG と CF、BF と BE は長さが等しくなります。これは、AE = AG、CG = CF、BF = BE を意味します。
プロパティ 2: 内心 私 三角形の角度とも特別な関係があります。これにより、角度 ∠BAI と ∠CAI が等しく、∠BCI と ∠ACI が等しく、∠ABI と ∠CBI が等しくなります。これは角の二等分定理に従います。
特性 3: 内心 私 は三角形の 3 辺すべてに接する円の中心であり、からの距離は 私 三角形の各辺 (EI、FI、GI) はすべて同じです。これらの距離は、内半径、または内接円の半径と呼ばれます。
特性 4: 半周長 (s) と半径 (r) を使用して三角形の面積を計算できます。式は A = sr です。ここで、A は面積、s は半周長 (s = (a + b + c)/2、a、b、c は三角形の辺の長さです)、r は半径内。
特性 5: 三角形の内心は常に三角形の内側にあります。場合によっては三角形の外側にある可能性がある垂心とは異なり、内心は常に三角形の境界内に含まれます。
三角形の公式の内心
3 つの座標 (x) を持つ式の内中心を見つける式1、 そして1)、 (バツ2、 そして2)、(x3、 そして3) は:
{(斧 1 +bx 2 +CX 3 )/(a + b + c)、(は 1 +によって 2 +c 3 )/(a + b + c)}
簡単に言えば、内中心を取得するには、次のようにします。
- 点 A の x 座標に辺の長さ a を乗算し、点 B の x 座標に辺の長さ b を乗算し、点 C の x 座標に辺の長さ c を乗算します。次に、これらを加算します。
- 結果を辺の長さ a、b、c の合計で割ります。
- y 座標についても同じプロセスを繰り返しますが、辺の長さ a、b、c を使用します。
三角形の内心 角度公式
三角形の角の内心を求める公式は次のとおりです。
三角形において、D、F、および G は、それぞれ角 A、B、および C の角の二等分線が辺 BC、AC、および AB と交わる点であるとします。
角度 ∠AIB (I は三角形の内心) は、次の式を使用して計算できます。
∠AIB = 180° – (角度 A と B の合計の半分)
または
∠AIB = 180° – (∠A + ∠B)/2
三角形の内心を見つける方法
三角形の内心を見つけるには 2 つの方法があります。構築では、三角形の角の二等分線を描いて内中心を見つけます。座標幾何学では、内心を決定する公式を使用します。
座標ジオメトリの使用 : A(2, 2)、B(6, 2)、および C(4, 5) として指定された座標で三角形の内心を見つけます。
与えられた情報によると
- (バツ1、 そして1) = (2, 2)
- (バツ2、 そして2) = (6, 2)
- (バツ3、 そして3) = (4, 5)
三角形の内心は次のようになります。
I(x, y) = {(斧 1 +bx 2 +CX 3 )/(a + b + c)、(は 1 +によって 2 +c 3 )/(a + b + c)}
辺 a の場合: 点 B と点 C の間の距離 = √((6 – 4)2+ (2 – 5)2) = √8
b 辺の場合: 点 A と点 C の間の距離 = √((2 – 4)2+ (2 – 5)2) = √13
辺 c の場合: 点 A と点 B の間の距離 = √((6 – 2)2+ (2 – 2)2) = 4
a、b、c の値を内心の公式に入れると、次のようになります。
I(x, y) = {(8×2 + 13×5 + 4×4)/(8 + 13 +4)、(8×2 + 13×2 + 4×5)/(8 + 13 +4) )}
⇒ I(x, y) = (16 + 78 + 16)/(25)、(16 + 26 + 20)/(25)
⇒ I(x, y) = (110/25, 62/25) = (22/5,62/25)
∴三角形ABCの内心は(22/5,62/25)の座標となります。
三角形の内心はどのように構築するか?
三角形の内中心を作成するには、コンパスを使用する必要があります。コンパスを使用して、以下の手順に従います。
ステップ1: コンパスの一端を三角形の頂点に置き、もう一端を一辺に接触させます。
ステップ2: コンパスを使用して、三角形の 2 つの辺に 2 つの円弧を描きます。
ステップ 3: コンパス上で同じ距離で、三角形の内側に 2 つの円弧を作成します。これらの円弧は、側面に接触する場所から互いに交差する必要があります。
ステップ 4: 三角形の頂点から内側の 2 つの円弧が交差する位置まで線を描きます。
ステップ5: 三角形のもう一方の頂点からも同じ手順を繰り返します。
ステップ6: 2 本の線が交わる、または交差する場所が三角形の内心になります。
直角三角形の内心
内心 直角三角形 直角三角形のすべての角の二等分線が交わる点です。直角三角形の辺が a、b、c である場合、内接円「r」の半径は r = (ab)/(a + b + c) として与えられます。直角三角形の内心は次のようになります。
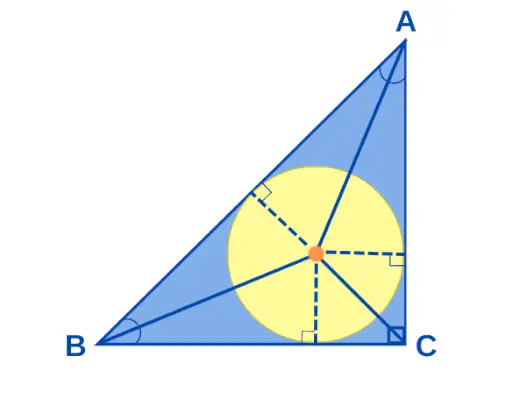
直角三角形の内心
重心、外心、内心、垂心
重心、外心、内心、垂心は、トレイングルに関連する 4 つの重要な点です。図心、外心、内心、直交中心の比較を以下の表に示します。
重心 | 中心付近 文字列をJSON Javaに変換 | 中心 | 直交中心 |
|---|---|---|---|
中央分離帯の交点 | 垂直二等分線の交点 | 角の二等分線の交点 | 高度の交差点 |
中央値を 2:1 で分割します | 三角形の外接円の中心 | 三角形の内接円の中心 | 直角三角形の垂心は直角です |
また、チェックしてください
- 三角形の面積
- 三角形の周囲長
- 三角形の角度の合計プロパティ
三角形の内心の例
例 1: 三角形 ABC の内心を計算します。 AB=8cm、BC=15cm、CA=17cm。
解決:
三角形の内心 = (aA + bB + cC)/(a + b + c) の公式を使用します。
どこ、
- a = 8
- b = 15
- c = 17
そして、角度は、
- A = 30°
- B = 60°
- ℃ = 90°
これらの値を計算式に代入すると、
⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}
⇒ (240 + 900 + 1530)/40
⇒ 2670/40
⇒ 66.75
zip用のLinuxコマンド
例 2: ジェーンは、三角形のフィールドの面積を 120 平方メートルと計算しました。フィールドの周囲は36メートルです。三角形の内側に円が三角形のすべての辺に接するように描かれている場合は、ジェーンが三角形の半径を計算するのを手伝ってください。
解決:
与えられた情報によると、
三角形の面積 = 120 平方メートル
三角形の周囲長 = 36 メートル
三角形の面積 = r × s がわかります。
s = 半周長
s = p/2 = 36/2 = 18
A = r × s
r = A/s
r = 120/18
r = 6.67 メートル
三角形の内心に関する練習問題
問題 1: 頂点 P(1, 2)、Q(4, 6)、および R(7, 2) を持つ三角形 PQR が与えられたとき、内心の座標を見つけます。
問題 2: ∠A = 45°、∠B = 60°、∠C = 75°の三角形 ABC を作図してください。作図法を使用して内中心を見つけます。
問題 3: 三角形 LMN において、∠L = 75°、∠M = 60°、∠N = 45°のとき、内心の座標を求めよ。
問題 4: ∠X = 80°、∠Y = 50°、∠Z = 50°の三角形 XYZ を作図してください。作図法を使用して内中心を見つけます。
三角形の内心: FAQ
三角形の内心とは何ですか?
三角形の内心は、内角の二等分線が交差する点です。三角形の 3 つの辺すべてから等距離にあります。
三角形の内心の意味は何ですか?
内心は、三角形の内接円、つまり三角形の内側に収まる最大の円の中心であるため、重要です。どの方向からも等距離にあるという性質があります。
内心は三角形の外側にある可能性がありますか?
いいえ、内心は常に三角形の内側にあります。これは角の二等分線の同時点であり、定義により、三角形の境界内になければなりません。
コンパスと直定規を使用して内心はどのように作成されますか?
内中心を作成するには、コンパスを使用して各頂点から反対側まで角の二等分線を描きます。内心は、これらの二等分線が交差する点です。
インセンター式とは何ですか?
三角形の内心の公式は次のように記述できます。
frac{(aA+bB+cC)}{a+b+c}
三角形の中心の性質とは何ですか?
内心にはいくつかの重要な特性があります。三角形の辺から等距離にあります。つまり、辺までの距離が等しいことを意味します。また、角を 2 等分する角の二等分線の交点でもあります。
インセンターはどのように決定されるのでしょうか?
内心を決定するには、角の二等分線が交差する場所を見つける必要があります。これは、内心の公式を使用するか、角の二等分線を描いてその交点を見つけることによって行うことができます。
インセンターと周囲中心の違いは何ですか?
内心と外心の主な違いは焦点です。内心は角の二等分線を扱い、内接円の中心です。外心は垂直二等分線を扱い、外接円の中心です。
インセンターとセントロイドは同じですか?
いいえ、内心と重心は異なります。内心は角の二等分線が交わる場所であり、図心は中央線が交差する場所です。中央線は頂点を反対側の中点に接続します。
インセンターとオルソセンターは同じですか?
いいえ、内心と垂心は同じではありません。内心は角度が互いに二等分する点であり、垂心には高度、つまり各頂点から反対側に垂直な線が含まれます。それらは三角形の異なる点です。
