この記事では、データ構造における順序トラバーサルについて説明します。
ノードを昇順で走査したい場合は、順序走査を使用します。順序トラバーサルに必要な手順は次のとおりです。
- 左側のサブツリー内のすべてのノードにアクセスします
- ルートノードにアクセスします
- 右側のサブツリー内のすべてのノードにアクセスします
スタック、配列、キューなどの線形データ構造には、データを走査する方法が 1 つしかありません。しかし、次のような階層データ構造では、 木、 データを走査するには複数の方法があります。ここでは、ツリー データ構造をトラバースする別の方法、つまり順序トラバーサルについて説明します。
順序トラバーサルには 2 つのアプローチが使用されます。
- 再帰を使用した順序トラバーサル
- 反復法を使用した順序トラバーサル
順序トラバーサル手法は次のとおりです。 左ルート右 ポリシー。ここで、Left Root Right は、ルート ノードの左側のサブツリーが最初にトラバースされ、次にルート ノードがトラバースされ、次にルート ノードの右側のサブツリーがトラバースされることを意味します。ここで、順序名自体は、ルート ノードが左右のサブツリーの間にあることを示唆しています。
再帰的手法と反復的手法の両方を使用した順序トラバーサルについて説明します。まず、再帰を使用した順序トラバーサルから始めましょう。
再帰を使用した順序トラバーサル
Step 1: Recursively traverse the left subtree Step 2: Now, visit the root Step 3: Traverse the right subtree recursively
順序トラバーサルの例
次に、順序トラバーサルの例を見てみましょう。例を使用すると、順序トラバーサルの手順が理解しやすくなります。
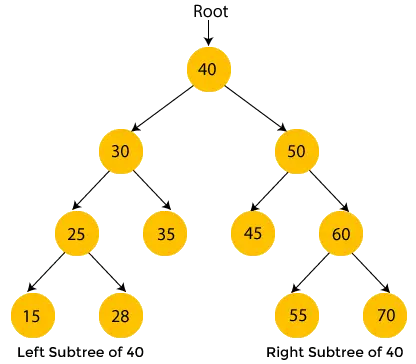
黄色のノードはまだ訪問されていません。ここで、順序トラバーサルを使用して上記のツリーのノードをトラバースします。
- ここで、40 はルート ノードです。 40 の左側のサブツリー、つまり 30 に移動します。これにはサブツリー 25 もあります。そのため、再び 25 の左側のサブツリー、つまり 15 に移動します。ここで、15 にはサブツリーがありません。 印刷15 そして親ノード 25 に向かって移動します。
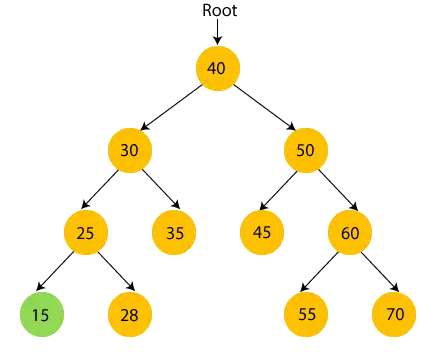
- 今、 プリント25 25 の右のサブツリーに移動します。
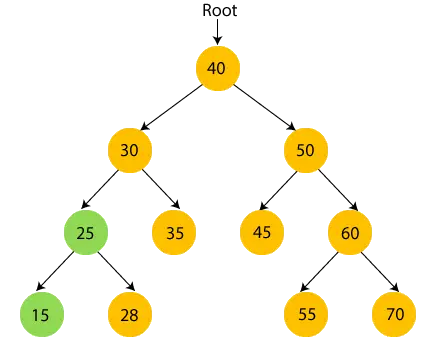
- 今、 プリント28 そして、25 のルート ノード、つまり 30 に移動します。
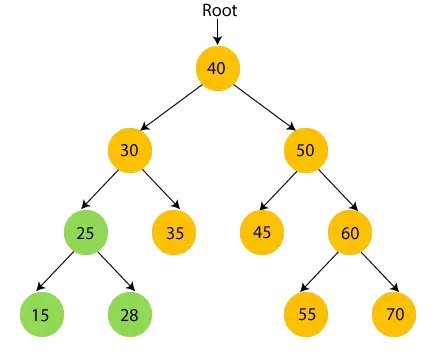
- したがって、30 の左側のサブツリーがアクセスされます。今、 印刷30 そして30の右の子に移動します。
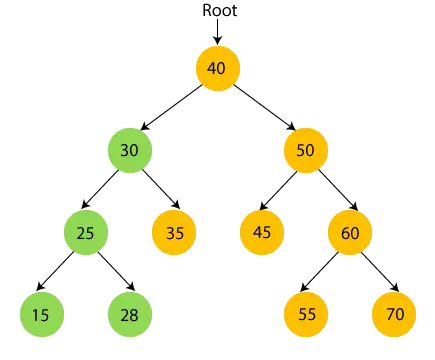
- 今、 プリント 35 そして 30 のルート ノードに移動します。
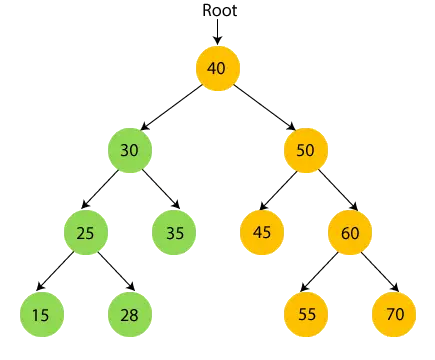
- 今、 ルートノード40を出力します そしてその右のサブツリーに移動します。
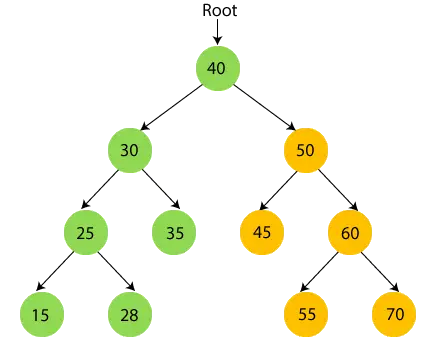
- ここで、40 の右側のサブツリー、つまり 50 を再帰的に走査します。
50 にはサブツリーがあるため、最初に 50 の左側のサブツリー、つまり 45 をたどります。45 には子がないため、 プリント45 そしてそのルートノードに移動します。
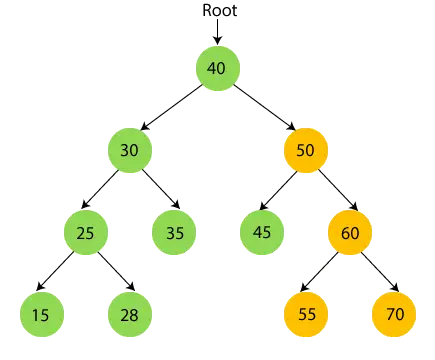
- 今 50を印刷する そして、50 の右のサブツリー、つまり 60 に移動します。
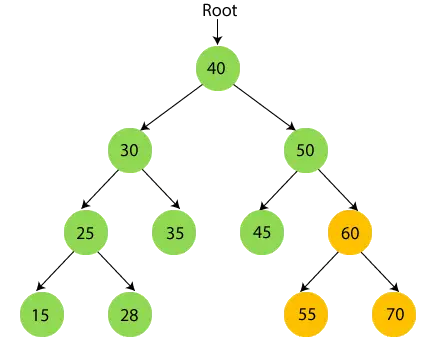
- 次に、50 の右側のサブツリー (60) を再帰的に走査します。60 にはサブツリーがあるため、最初に 60 の左側のサブツリー (55) を走査します。55 には子がありません。 プリント55 そしてそのルートノードに移動します。
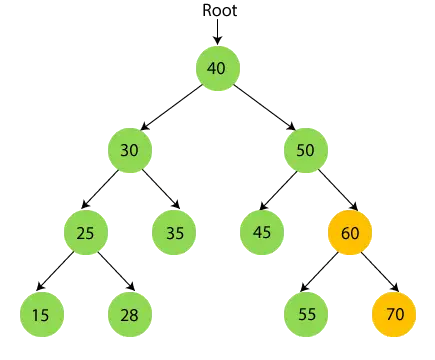
- 今 プリント60 そして 60 の右のサブツリー、つまり 70 に移動します。
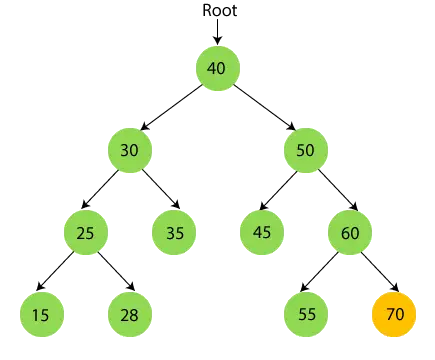
- 今 70を印刷します。
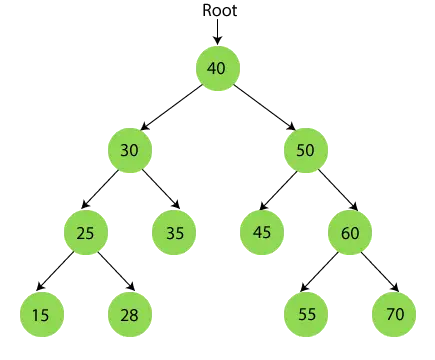
順序トラバーサルの完了後の最終出力は -
{15、25、28、30、35、40、45、50、55、60、70}
インオーダートラバーサルの複雑さ
インオーダートラバーサルの時間計算量は次のとおりです。 の上)、 ここで、「n」はバイナリ ツリーのサイズです。
一方、順序トラバーサルの空間複雑さは ○(1)、 関数呼び出しのスタック サイズを考慮しない場合。それ以外の場合、順序トラバーサルの空間複雑さは次のようになります。 おお)、 ここで、「h」は木の高さです。
インオーダートラバーサルの実装
次に、さまざまなプログラミング言語での順序トラバーサルの実装を見てみましょう。
プログラム: インオーダートラバーサルを実装するプログラムをC言語で書きます。
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); return 0; } 出力

プログラム: C++ でインオーダー トラバーサルを実装するプログラムを作成します。
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } int main() { struct node* root="createNode(39);" root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the inorder traversal of given binary tree is -
'; traverseinorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-14.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(36); bt.root.left = new Node(26); bt.root.right = new Node(46); bt.root.left.left = new Node(21); bt.root.left.right = new Node(31); bt.root.left.left.left = new Node(11); bt.root.left.left.right = new Node(24); bt.root.right.left = new Node(41); bt.root.right.right = new Node(56); bt.root.right.right.left = new Node(51); bt.root.right.right.right = new Node(66); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-15.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-16.webp" alt="Inorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> 出力

プログラム: Java でインオーダー トラバーサルを実装するプログラムを作成します。
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } 出力

それでは、この記事については以上です。この記事があなたにとって有益で有益であることを願っています。











