あ 有向非巡回グラフ 、と略されることがよくあります。 日 、グラフ理論の基本的な概念です。 DAG 物事がどのように相互に関連しているか、または相互に依存しているかを明確かつ組織的に示すために使用されます。この記事では、次のことを学びます。 有向非巡回グラフ 、その特性、および実生活での応用について説明します。

有向非巡回グラフ
有向非巡回グラフとは何ですか?
あ 有向非巡回グラフ (DAG) はサイクルを含まない有向グラフです。
以下のグラフは、有向非巡回グラフ (DAG) を表しています。

直接非巡回グラフ
有向非巡回グラフの意味:
有向非巡回グラフには 2 つの重要な機能があります。
- 有向エッジ s:有向非巡回グラフでは、 各エッジには方向があり、ある頂点 (ノード) から別の頂点 (ノード) に向かうことを意味します。この方向は、 一方通行 ノード間の関係または依存関係。
- 非環状: 用語 非周期的な グラフ内にサイクルや閉ループがないことを示します。つまり、エッジの方向に従って、一連の有向エッジを横断して同じノードに戻ることはできません。サイクルの形成は禁止されています 日。 したがって、この特性は不可欠です。

有向非巡回グラフ
有向非巡回グラフ DAG のプロパティ:
有向非巡回グラフ (DAG) には、グラフ問題で使用できるようにするさまざまなプロパティがあります。
有向非巡回グラフ (DAG) には次のプロパティがあります。
- 到達可能性の関係: DAG では、2 つのノード間に到達可能性関係があるかどうかを判断できます。ノード B から始まりノード A で終わる有向パスが存在する場合、ノード A はノード B から到達可能であると言われます。これは、グラフ内のエッジの方向に従って B から A に到達できることを意味します。
- 推移的閉包: 有向グラフの推移閉包は、元のグラフ内のノード間のすべての直接的および間接的な関係または接続を表す新しいグラフです。言い換えれば、1 つ以上の有向エッジをたどることで他のノードからどのノードに到達できるかを示します。
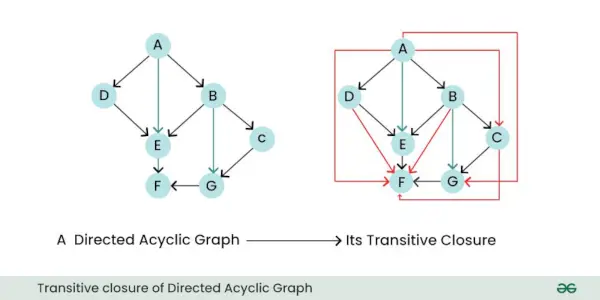
有向非巡回グラフの推移閉包
- 推移的還元: 有向グラフの推移的リダクションは、不要な間接的なエッジを削除しながら、ノード間の重要な直接的な関係のみを保持する新しいグラフです。基本的に、残りのエッジから推測できるエッジを削除することでグラフを簡素化します。
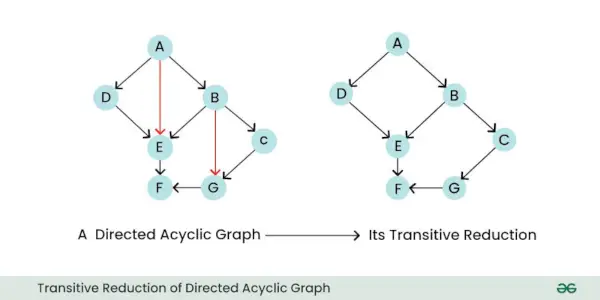
有向非巡回グラフの推移的還元
- トポロジカルな順序付け: DAG はトポロジー的に並べ替えることができます。つまり、すべてのエッジについて、エッジの開始ノードがシーケンスの最初に現れるようにノードを線形に並べることができます。このプロパティは、スケジュールや依存関係の解決などのタスクに役立ちます。
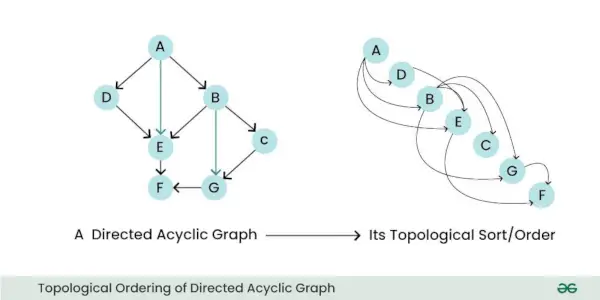
有向非巡回グラフのトポロジー的順序付け
DAG の実際の応用例:
- データフロー分析: コンパイラーの設計と最適化では、プログラム内のデータ フローを表すために DAG が使用されます。これは、冗長な計算や無効なコードを特定することにより、コードの最適化に役立ちます。 DAG は、次の構造を表すためにも使用されます。 基本ブロック コンパイラ設計で。
- タスクのスケジュール設定: DAG は、プロジェクト管理とジョブのスケジューリングに使用されます。各タスクまたはジョブは、依存関係を示す有向エッジを備えた DAG 内のノードとして表されます。 DAG の非周期的な性質により、タスクが論理的な順序でスケジュールされ、循環依存関係が防止されます。
重み付き有向非巡回グラフを使用して、スケジューリング問題を表現できます。タスクのスケジュールの問題の例を見てみましょう。ここで、頂点はタスクを表すことができ、その重みはタスクの計算のサイズを表すことができます。同様に、エッジは 2 つのタスク間の通信を表すことができ、その重みは通信のコストを表すことができます。
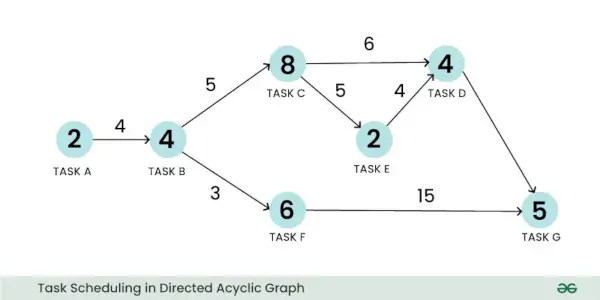
有向非巡回グラフでのタスクのスケジューリング
結論:
要約すると、有向非巡回グラフは、数多くの実際的な応用が可能なグラフ理論の基本概念です。 DAG は、タスクのスケジューリング、データ フロー分析、依存関係の解決、およびコンピューター サイエンスとエンジニアリングのその他のさまざまな分野で重要な役割を果たします。これらは、プロセスの最適化、依存関係の管理、タスクやジョブの効率的な実行の確保に役立ちます。
