logo

TechCodeview

有限オートマトンの紹介

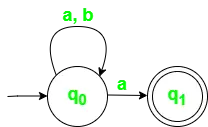
有限オートマトン (FA) は、パターンを認識する最も単純なマシンです。通常の言語 (/baa+!/ など) を特徴付けるために使用されます。
また、自然言語表現の分析と認識にも使用されます。有限オートマトンまたは有限状態マシンは、5 つの要素またはタプルを持つ抽象マシンです。これには、ある状態から別の状態に移行するための一連の状態とルールがありますが、適用される入力シンボルによって異なります。状態と一連のルールに基づいて、入力文字列を受け入れるか拒否することができます。基本的に、これは入力文字列を読み取り、現在の入力シンボルに応じて内部状態を変更するデジタル コンピューターの抽象モデルです。すべてのオートマトンは言語、つまり受け入れる文字列のセットを定義します。次の図は、一般的な自動化の重要な機能をいくつか示しています。

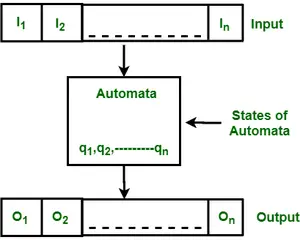
形： 有限オートマトンの特徴



上の図は、オートマトンの次の機能を示しています。

  1. 入力
  2. 出力
  3. オートマトンの状態
  4. 状態関係
  5. 出力関係

有限オートマトンは次のもので構成されます。

PowerShell の複数行コメント 
Q : Finite set of states. ? : set of Input Symbols. q : Initial state. F : set of Final States. ? : Transition Function.>

機械の正式な仕様は、



{ Q, ?, q, F, ? }>

FA は 2 つのタイプに分類されます。

1) 決定論的有限オートマトン (DFA): 

DFA consists of 5 tuples {Q, ?, q, F, ?}. Q : set of all states. ? : set of input symbols. ( Symbols which machine takes as input ) q : Initial state. ( Starting state of a machine ) F : set of final state. ? : Transition Function, defined as ? : Q X ? -->Q.>

DFA では、特定の入力文字に対して、マシンは 1 つの状態のみになります。遷移関数は、すべての入力シンボルのすべての状態に対して定義されます。また、DFA では null (または ?) 移動は許可されません。つまり、DFA は入力文字なしで状態を変更できません。



Javaのコレクション

たとえば、「a」で終わるすべての文字列の言語を受け入れる DFA を構築します。
与えられた条件: ? = {a,b}、q = {q0}、F={q1}、Q = {q0、q1}

まず、正確な状態遷移図を構築するために、可能なすべての受け入れ可能な文字列の言語セットを検討します。
L = {a、aa、aaa、aaaa、aaaa、ba、bba、bbba、父、父、父、父}
上記は、受け入れ可能な文字列の単純なサブセットであり、「a」で終わり、記号 {a,b} を含む他の多くの文字列が存在する可能性があります。

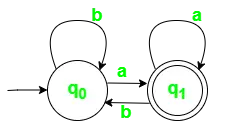
図 1. ? を使用した DFA の状態遷移図= {a, b}

受け入れられない文字列は、
ab、bb、aab、abb など。

上記オートマトンの状態遷移表、

？州シンボル？ ある b
q0 q1 q0
q1 q1 q0

注意すべき重要な点が 1 つあります。 パターンには多くの DFA が考えられます 。一般に、状態の数が最小限の DFA が推奨されます。

2) 非決定性有限オートマトン(NFA): NFA は、次の追加機能を除いて DFA に似ています。

  1. Null (または ?) 移動が許可されます。つまり、シンボルを読み取らずに先に進むことができます。
  2. 特定の入力に対して任意の数の状態に送信する機能。

ただし、上記の機能は NFA を強化するものではありません。両者をパワーで比較すると、どちらも同等です。

Linuxコマンドのディレクトリ

上記の追加機能により、NFA には異なる移行機能がありますが、残りは DFA と同じです。

?: Transition Function ?: Q X (? U ? ) -->2 ^ Q.>> 
遷移関数が null (または ?) を含む任意の入力に対して行われていることからわかるように、NFA は任意の数の状態に進むことができます。たとえば、以下は上記の問題に対する NFA です。
  
図 2. ? を使用した NFA の状態遷移図= {a, b}
 
上記オートマトンの状態遷移表、
 
 
 ？州シンボル？ ある b 
  
 q0 {q0、q1} q0 
 
 q1 ? ? 
  
 
注意すべき重要な点が 1 つあります。   NFA では、入力文字列のいずれかのパスが最終状態につながる場合、入力文字列は     は     受け入れられました   。たとえば、上記の NFA では、入力文字列 00 に対して複数のパスが存在します。パスの 1 つが最終状態につながるため、上記の NFA では 00 が受け入れられます。
 
  重要な点:  
トップ 10 エロアニメ

 
    理由:
DFA と NFA のすべてのタプルは、遷移関数 (?) であるタプルの 1 つを除いて同じであるため、