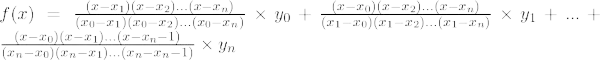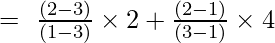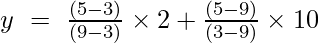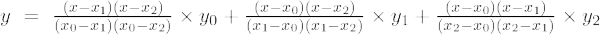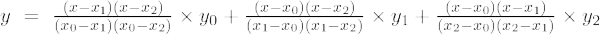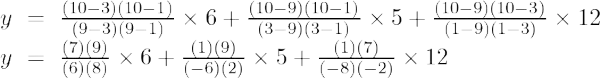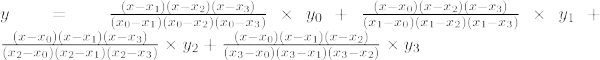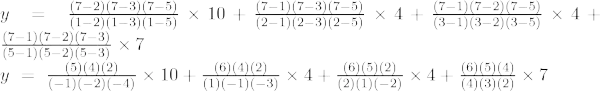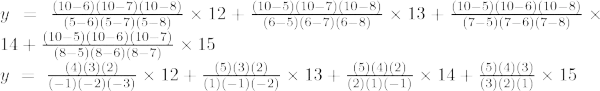ラグランジュ補間公式: 証明、例、および FAQ

ラグランジュ補間式 任意の点で特定の値を取るラグランジュ多項式と呼ばれる多項式を見つけます。それはn級です関数 f(x) の多項式表現。内挿法は、既知のデータポイントの離散セットの範囲内で新しいデータポイントを見つけるために使用されます。

この記事では、ラグランジュ補間、ラグランジュ補間公式、ラグランジュ補間公式の証明、ラグランジュ補間公式に基づく例などについて詳しく学びます。

ラグランジュ補間とは何ですか?

ラグランジュ補間は、関数が指定されていない場合に、任意の点での関数の値を見つける方法です。関数上の他のポイントを使用して、必要なポイントで関数の値を取得します。

x の値を代入すると y の異なる値が得られる関数 y = f(x) があるとします。そして 2 点が与えられます (x₁、そして₁) と (x₂、そして₂) 曲線上で x = a(定数) における y の値がラグランジュ補間公式を使用して計算されます。

ラグランジュ補間式

実数値がほとんどない場合 x₁、バツ₂、バツ₃、 …、バツ_nそしてy₁、そして₂、そして₃、 …、そして_nそして、条件を満たす実係数を持つ多項式 P が存在します P(x_私) = そして_私、 ∀ i = {1, 2, 3, …, n} であり、多項式 P の次数は実数値の数、つまりdegree(P) より小さくなければなりません。

n次のラグランジュ補間式

n のラグランジュ補間式^番目次数多項式は次のように与えられます。

n のラグランジュ補間式 ^番目 順序は、

$f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} imes y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n$

ラグランジュ一次補間式

もし多項式の次数が 1 の場合、一次多項式と呼ばれます。 1のラグランジュ補間式^セント次数多項式は、

$f(x)~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1$

ラグランジュ二次補間式

多項式の次数が 2 の場合、それは 2 次多項式と呼ばれます。 2 次多項式のラグランジュ補間公式は次のとおりです。

$f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2$

ラグランジュ定理の証明

与えられた形式の n 次多項式を考えてみましょう。

f(x) = A₀(x – x₁)(x – x₂)(x – x₃)…(x – x_n) + A₁(x – x₁)(x – x₂)(x – x₃)…(x – x_n) + … + A_(n-1)(x – x₁)(x – x₂)(x – x₃)…(x – x_n)

代替観測値 x_私Aを取得する_私

x = x と置きます₀それからAを取得します₀

f(x₀) = そして₀=A₀（バツ₀- バツ₁）（バツ₀- バツ₂）（バツ₀- バツ₃）…（バツ₀- バツ_n)

あ ₀ = そして ₀ /（バツ ₀ - バツ ₁ ）（バツ ₀ - バツ ₂ ）（バツ ₀ - バツ ₃ ）…（バツ ₀ - バツ _n )

x = x を代入すると₁Aを取得します₁

f(x₁) = そして₁=A₁（バツ₁- バツ₀）（バツ₁- バツ₂）（バツ₁- バツ₃）…（バツ₁- バツ_n)

あ ₁ = そして ₁ /（バツ ₁ - バツ ₀ ）（バツ ₁ - バツ ₂ ）（バツ ₁ - バツ ₃ ）…（バツ ₁ - バツ _n )

同様に、x = x を代入すると、_nAを取得します_n

f(x_n) = そして_n=A_n（バツ_n- バツ₀）（バツ_n- バツ₁）（バツ_n- バツ₂）…（バツ_n- バツ_n-1)

あ _n = そして _n /（バツ _n - バツ ₀ ）（バツ _n - バツ ₁ ）（バツ _n - バツ ₂ ）…（バツ _n - バツ _n-1 )

A のすべての値を代入すると_私関数 f(x) (i = 1, 2, 3, …n) では、次のようなラグランジュ補間式が得られます。

$f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)}回 y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)}回 y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n$

ラグランジュ補間式の性質

ラグランジュ補間式のさまざまなプロパティについては以下で説明します。

この公式は、関数自体が指定されていない場合でも、任意の時点で関数の値を見つけるために使用されます。
与えられたポイントが等間隔でない場合でも使用されます。
これは、任意の関数に属する独立変数の従属変数の値を与えるため、関数の値を見つけるための数値解析などで使用されます。

ラグランジュ補間公式の使用法

ラグランジュ補間公式のさまざまな使用法については以下で説明します。

これは、関数自体が指定されていない場合でも、特定の独立変数で従属変数の値を見つけるために使用されます。
画像のスケーリングに使用されます。
AIモデリングに利用されています。
NLPなどを教えるために使用されます。

続きを読む、

補間式
直線補間式

ラグランジュ補間式の使用例

ラグランジュ補間公式に関するいくつかのサンプル質問を見てみましょう。

例 1: 指定された点のセット (1, 2)、(3, 4) について、x = 2 における y の値を求めます。

解決：

考えると、

（バツ₀、そして₀) = (1, 2)
（バツ₁、そして₁) = (3, 4)
一次ラグランジュ補間式は、

$y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1$

x = 2 の場合

そして $=~frac{(2-3)}{(1-3)} imes 2+frac{(2-1)}{(3-1)} imes 4$

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

x = 2 における y の値は 3 です

例 2: 指定された点セット (9, 2)、(3, 10) について、x = 5 における y の値を求めます。

解決：

考えると、

（バツ₀、そして₀) = (9, 2)
（バツ₁、そして₁) = (3, 10)
一次ラグランジュ補間式は、

$y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1$

x = 5 の場合

$y~=~frac{(5-3)}{(9-3)} imes 2+frac{(5-9)}{(3-9)} imes 10$

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7.33

x = 5 における y の値は 7.33 です。

例 3: 指定された点セット (1, 6)、(3, 4)、(2, 5) について、x = 1 における y の値を求めます。

エース対デス

解決：

考えると、

（バツ₀、そして₀) = (1, 6)
（バツ₁、そして₁) = (3, 4)
（バツ₂、そして₂) = (2, 5)
二次ラグランジュ補間式は、

$y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1) -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2$

x = 1 の場合

$y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} imes 6+frac{(1-1)(1-2)}{( 3-1)(3-2)} imes 4+frac{(1-1)(1-3)}{(2-1)(2-3)} imes 5 y~=~ frac{(-2)(-1)}{(-2)(-1)} imes 6+frac{(0)(-1)}{(2)(1)} imes 4+frac {(0)(-2)}{(1)(-1)} imes 5$

y = (12/2) + 0 + 0

y = 6
mysqlワークベンチの使い方

x = 1 における y の値は 6 です

例 4: 指定された点のセット (9, 6)、(3, 5)、(1, 12) について、x = 10 における y の値を求めます。

解決：

考えると、

（バツ₀、そして₀) = (9, 6)
（バツ₁、そして₁) = (3, 5)
（バツ₂、そして₂) = (1, 12)
二次ラグランジュ補間式は、

$y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1) -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2$

x = 10 の場合

$y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} imes 6+frac{(10-9)(10-1)}{( 3-9)(3-1)} imes 5+frac{(10-9)(10-3)}{(1-9)(1-3)} imes 12 y~=~ frac{(7)(9)}{(6)(8)} imes 6+frac{(1)(9)}{(-6)(2)} imes 5+frac{(1) (7)}{(-8)(-2)} imes 12$

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9.375

x = 10 における y の値は 9.375 です。

例 5: 指定された点セット (1, 10)、(2, 4)、(3, 4)、(5, 7) について、x = 7 における y の値を求めます。

解決：

考えると、

（バツ₀、そして₀) = (1, 10)
（バツ₁、そして₁) = (2, 4)
（バツ₂、そして₂) = (3, 4)
（バツ₃、そして₃) = (5, 7)
三次ラグランジュ補間式は、

$y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)} imes y_3$

x = 7 で

$y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)} imes 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)} imes 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)} imes 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)} imes 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)} imes 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} imes 4+frac{(6)(5)(2)}{(2)(1) (-2)} imes 4+frac{(6)(5)(4)}{(4)(3)(2)} imes 7$

y = -50 + 64 – 60 + 35

y = 99 – 110 = -十一

x = 7 における y の値は -11 です

例 6: 指定された点セット (5, 12)、(6, 13)、(7, 14)、(8, 15) について、x = 10 における y の値を求めます。

解決：

考えると、

（バツ₀、そして₀) = (5, 12)
（バツ₁、そして₁) = (6, 13)
（バツ₂、そして₂) = (7, 14)
（バツ₃、そして₃) = (8, 15)
三次ラグランジュ補間式は、

$y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)} imes y_3$

x = 10 の場合、

$y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)} imes 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)} imes 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)} imes 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)} imes 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)} imes 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} imes 13+frac{(5)(4)(2)}{(2)(1) (-1)} imes 14+frac{(5)(4)(3)}{(3)(2)(1)} imes 15$

y = -48 + 195 – 280 + 150

y = 17

x = 10 における y の値は 17 です

例 7: 指定された点のセット (-2, 5),(1, 7) について、x = 0 における y の値を求めます。

解決：

考えると、

（バツ₀、そして₀) = (-2, 5)
（バツ₁、そして₁) = (1, 7)
一次ラグランジュ補間式は、

$y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1$

x = 0 では、

$y~=~frac{(0-1)}{(-2-1)} imes 5+frac{(0+2)}{(1+2)} imes 7$

y = (5/3) + (14/3)

y = 19/3 = 6.33

x = 0 における y の値は 6.33 です。

ラグランジュ補間式に関する FAQ

1. ラグランジュ補間公式とは何ですか?

ラグランジュ補間公式は、関数自体が与えられていなくても、任意の独立変数に対する関数の従属変数の値を見つけるために使用される公式です。

2. ラグランジュ補間公式の応用例は何ですか?

ラグランジュの公式は、現代の数学やデータサイエンスでさまざまな応用が可能です。

AIモデルのトレーニングに使用されます。
画像処理に使用されます。
3 次元以上の曲線のグラフ作成などに使用されます。

3. 一次ラグランジュ補間公式とは何ですか?

一次ラグランジュ補間公式は次のとおりです。

f(x) = (x – x ₁ ）/（バツ ₀ - バツ ₁ )×f ₀ + (x – x ₀ ）/（バツ ₁ - バツ ₀ )×f ₁

4. 2次ラグランジュ補間公式とは何ですか?

2 次ラグランジュ補間公式は次のとおりです。

f(x) = [(x – x ₁ )(x – x ₂ ）/（バツ ₀ - バツ ₁ ）（バツ ₀ - バツ ₂ )]×f ₀ + [(x – x ₀ )(x – x ₂ ）/（バツ ₁ - バツ ₀ ）（バツ ₁ - バツ ₂ )]×f ₁ + [(x – x ₀ )(x – x ₁ ）/（バツ ₂ - バツ ₀ ）（バツ ₂ - バツ ₂ )]×f ₀