線形計画 は、一次関数の最適解を見つけるために使用される数学的概念です。この方法では、単純な仮定を使用して特定の関数を最適化します。線形計画法は現実世界で非常に応用されており、さまざまなタイプの問題を解決するために使用されます。
線形計画法は、海運業、製造業、運輸業、通信業など、さまざまな業界で活用されています。
線形計画という用語は、線形とプログラミングという 2 つの単語で構成されています。線形という単語は、問題で使用される次数のさまざまな種類の変数間の関係を示し、プログラミングという単語は、これらの問題を解決するための段階的な手順を示します。
この記事では、線形計画法、その例、公式、その他の概念について詳しく学びます。
目次
- 線形計画法とは何ですか?
- 線形計画法のコンポーネント
- 線形計画法の例
- 線形計画法の問題
- 線形計画問題の種類
- 線形計画法
- 線形計画法の問題を解くには?
- 線形計画法
- 線形計画法シンプレックス法
- 線形計画法によるグラフィカルな手法
- 線形計画法の応用
- 線形計画法の重要性
- 線形計画法の最新のアプリケーション
- オペレーションズ リサーチにおける線形計画法
- シンプレックス法
線形計画法とは何ですか?
線形計画 または 線形最適化 は、与えられた問題に対する最適な解決策を見つけるのに役立つテクニックであり、最適な解決策とは、与えられた特定の問題の可能な限り最善の結果となる解決策です。
簡単に言えば、何かをできる限り最善の方法で行う方法を見つける方法です。限られたリソースでは、リソースを最適に利用し、最小コスト、最大マージン、最小時間などの特定の目的で可能な限り最高の結果を達成する必要があります。
特定の制約の下で変数の最適な値を検索する必要がある状況では、線形計画問題が使用されます。このような状況は、通常の微積分や数値手法では対処できません。
線形計画法の定義
線形計画法は、特定のシナリオを最適化するために使用される手法です。線形計画法を使用すると、特定の状況で可能な限り最良の結果が得られます。利用可能なすべてのリソースが最適な結果を生み出すような方法で使用されます。
線形計画法のコンポーネント
線形計画法 (LP) 問題の基本コンポーネントは次のとおりです。
- 決定変数: 最適なソリューションを実現するために決定する必要がある変数。
- 目的関数: M 達成したい目標を表す数式
- 制約: 決定変数が従わなければならない制限または制限。
- 非否定的な制限: 一部では 現実世界のシナリオでは、決定変数を負にすることはできません
線形計画法の追加の特徴
- 有限性: LP 問題における決定変数と制約の数は有限です。
- 直線性: 目的関数とすべての制約は決定変数の線形関数でなければなりません 。 これは、変数の次数が 1 である必要があることを意味します。
線形計画法の例
以下で説明する例を参考にすると、線形計画法が適用される状況を理解できます。
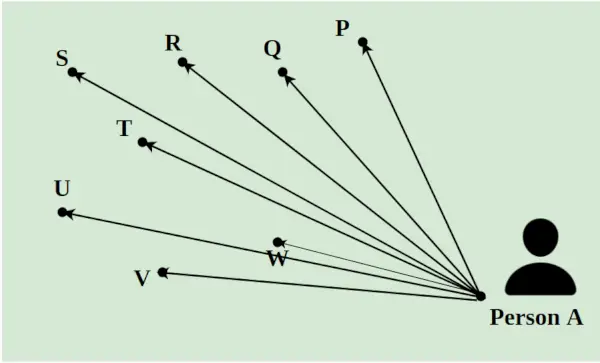
配達員が 1 日に 8 個の荷物を市内のさまざまな場所に配達しなければならないとします。彼は A からすべてのパケットを選択し、それらをポイント P、Q、R、S、T、U、V、および W に配信する必要があります。それらの間の距離は、下の図に示すように線を使用して示されます。配達員がたどる最短経路は、線形計画法の概念を使用して計算されます。
太字のCSS
線形計画法の問題
線形計画問題 (LPP) 線形関数を最適化して、関数の最適値の解を見つけることが含まれます。最適値は、最大値または最小値のいずれかになります。
LPP では、線形関数は次のように呼ばれます。 目的関数。 目的関数には複数の変数を含めることができ、これらの変数には条件が適用され、次の条件を満たす必要があります。 線形制約 。
線形計画問題の種類
さまざまな線形計画問題 (LPP) がありますが、この記事では 3 つの主要な線形計画問題を扱います。
製造上の問題
製造上の問題は、各製品が一定の人員、機械時間、および原材料を必要とする場合に、利益を最大化するために生産または販売する必要があるユニットの数を扱う問題です。
食事の問題
これは、食料の入手可能性とその価格に応じて、最小コストを得るために食事に含まれるさまざまな種類の成分の数を計算するために使用されます。
輸送の問題
これは、異なる場所にある工場/工場から異なる市場に製品を輸送する最も安価な方法を見つける輸送スケジュールを決定するために使用されます。
線形計画法
線形計画問題は次のもので構成されます。
- 決定変数
- 目的関数
- 制約
- 非ネガティブな制限
決定変数 は変数 x と y で、線形計画問題の出力を決定し、最終的な解を表します。
の 目的関数 一般に Z で表される線形関数は、最終的な解を得るために指定された条件に従って最適化する必要があります。
の 制限 値を制限する決定変数に課されるものは、制約と呼ばれます。
さて、線形計画問題の一般式は次のとおりです。
目的関数 : Z = 斧 + によって
制約: cx + dy ≥ e、px + qy ≤ r
否定的でない制限: x ≥ 0、y ≥ 0
上記の条件では、x と y が決定変数です。
線形計画法の問題を解くには?
線形計画問題を解く前に、まず標準パラメータに従って問題を定式化する必要があります。線形計画問題を解く手順は次のとおりです。
ステップ1: 問題内の決定変数をマークします。
ステップ2: 問題の目的関数を構築し、関数を最小化する必要があるか最大化する必要があるかを確認します。
ステップ 3: 線形問題の制約をすべて書き留めます。
ステップ 4: 決定変数に負の制限がないことを確認します。
ステップ5: ここで、一般にシンプレックス法またはグラフィカル法を使用する任意の方法を使用して線形計画問題を解きます。
線形計画法
私たちは線形計画問題を解決するためにさまざまな方法を使用します。最も一般的に使用される 2 つの方法は次のとおりです。
- シンプレックス法
- グラフィカルな方法
この記事では、これら 2 つの方法について詳しく学びましょう。
線形計画法シンプレックス法
線形計画問題を解くための最も一般的な方法の 1 つはシンプレックス法です。この方法では、最適な解が得られるまで、特定の条件「n」を何度も繰り返します。
シンプレックス法を使用して線形計画問題を解くために必要な手順は次のとおりです。
ステップ1: 与えられた制約に基づいて線形計画問題を定式化します。
ステップ2: 必要に応じて各不等式にスラック変数を追加することにより、指定されたすべての不等式を線形計画問題の方程式または等式に変換します。
ステップ 3: 初期シンプレックス テーブルを構築します。各制約式を一行で表し、目的関数を一番下の行に書きます。このようにして得られたテーブルは、シンプレックス テーブルと呼ばれます。
ステップ 4: 一番下の行で最大の負のエントリを特定します。最大の負のエントリを持つ要素の列はピボット列と呼ばれます。
ステップ5: 最下行のエントリを除く、右端の列のエントリをそれぞれのピボット列のエントリで分割します。現在、最も少ないエントリを含む行はピボット行と呼ばれます。ピボット要素は、ピボット行とピボット列の交差によって取得されます。
ステップ6: 行列演算を使用し、ピボット要素を利用すると、ピボット列のすべてのエントリがゼロになります。
ステップ 7: 最下行の非負のエントリを確認し、最下行に負のエントリがない場合はプロセスを終了し、そうでない場合は手順 4 からプロセスを再度開始します。
ステップ8: こうして得られた最終的なシンプレックス テーブルにより、問題の解決策が得られます。
線形計画法によるグラフィカルな手法
グラフィカル手法は、線形計画問題を解くために使用されるシンプレックス手法とは別の手法です。名前が示すように、このメソッドはグラフを使用して、指定された線形計画問題を解決します。これは線形計画法の問題を解決するための最良の方法であり、シンプレックス法よりも少ない労力で済みます。
この方法を使用すると、指定された線形計画問題で制約を受けるすべての不等式がプロットされます。指定された LPP のすべての不等式が XY グラフにプロットされるとすぐに、すべての不等式の共通領域が最適解を与えます。実行可能領域のすべてのコーナーポイントが計算され、それらすべてのポイントにおける目的関数の値が計算され、これらの値を比較して、LPP の最適解が得られます。
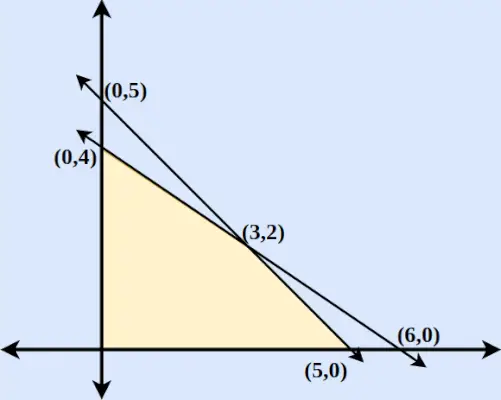
例: 制約条件が次の場合、z = 6x + 9y の最大値と最小値を求めます。
- 2x + 3y ≤ 12
- x と y ≥ 0
- x + y ≤ 5
解決:
ステップ1 : まず不等式を正規方程式に変換します。したがって、方程式は 2x+3y = 0、x = 0、y = 0、x + y = 5 となります。
ステップ2 : 2x + 3y および x + y = 5 が x 軸と y 軸を切る点を見つけます。 x 軸の交点を見つけるには、それぞれの方程式に y = 0 を入力して点を見つけます。同様に、y 軸の交点についても、それぞれの式に x = 0 を入力します。
ステップ3 :x軸とy軸を切る2本の線を描きます。 2 つの軸が (3,2) で交差していることがわかります。
ステップ4 : x ≥ 0 および y ≥ 0 の場合、両方の不等式が成り立つことがわかります。したがって、領域には、原点を含む 2 つの軸と両方の線で囲まれた面積領域が含まれます。プロットされた領域は図の下に示されています。
ステップ5 : 各点の Z と最大値と最小値を求めます。
座標 Z = 6x + 9y (0.5) Z = 45 (0.4) Z = 36 (5.0) Z = 30 (6.0) Z = 36 (3.2) Z = 36 したがって、Z = 6x + 9y は (0,5) で最大となり、(5,0) で最小になることがわかります。
線形計画法の応用
線形計画法はさまざまな分野で応用されています。これは、問題のすべての制約が与えられた場合のプロセスの最小コストを見つけるために使用されます。車両の輸送コストの最適化などに利用されます。線形計画法のさまざまな応用例が挙げられます。
エンジニアリング産業
エンジニアリング業界は、線形計画法を使用して設計および製造の問題を解決し、特定の条件から最大の出力を引き出します。
製造業
製造業は、企業の利益を最大化し、製造コストを削減するために線形計画法を使用します。
エネルギー産業
エネルギー会社は線形計画法を使用して生産量を最適化します。
運輸産業
線形計画法は、輸送コストを最小限に抑える方法を見つけるために輸送業界でも使用されます。
線形計画法の重要性
線形計画法は、さまざまな業界で非常に重要であり、さまざまな制約に従って入力値を最小限に抑えながら出力値を最大化します。
LP は、問題を解決する際に複数の条件があり、問題の出力を最適化する必要がある場合、つまり、特定の条件に従って最小値または最大値を見つける必要がある場合に非常に適しています。
続きを読む、
- 線形不等式
- 線形不等式の代数的解法
線形計画法の問題
問題 1: ある会社が 2 種類の製品を製造および販売しており、各ユニット a と b の製造原価はそれぞれ 200 ルピーと 150 ルピーです。製品の各ユニットの販売利益は 20 ルピーで、製品 b の各ユニットの販売利益は 15 ルピーです。 。同社は、A と B の月間需要が、その月の生産予算全体の最大収穫ユニット数であると推定し、50,000 ルピーに設定されています。企業は、A と B の月次売上から最大の利益を得るには、何ユニットを製造する必要があります。そしてb?
解決:
x = タイプ A のユニット数とする
y = タイプ B のユニット数
Z = 40x + 50y を最大化
制約の対象となる
3x + y ≤ 9
x + 2y ≤ 8
そしてx、y ≥ 0
方程式を考えてみましょう。
3x + y = 9
x = 3
y = 0
そしてx + 2y = 8
x = 8
y = 0
ここで、4 つの点 (頂点) での Z の値を評価することで、Z の最大値を決定できます。以下に示します。
頂点
Z = 40x + 50y
(0, 0)
rrアルゴリズムZ = 40 × 0 + 50 × 0 = Rs. 0
(3,0)
Z = 40 × 3 + 50 × 0 = Rs. 120
(0、4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(23)
Z = 40 × 2 + 50 × 3 = Rs. 230
最大利益、Z = Rs。 230
∴Aタイプの台数は2台、Bタイプの台数は3台となります。
問題 2: Z = 3x + 4y を最大化します。
x + y ≤ 450、2x + y ≤ 600、および x、y ≤ 0 という制約に従います。
解決:
私たちは与えられたものから持っています
制約 (1)
X + Y = 450
x = 0 とすると、 ⇒ 0 + y = 450 ⇒ y = 450
y = 0とすると、 ⇒ x + 0 = 450 ⇒ x = 450
から、 制約 (2)
2x + y = 600
x = 0 とすると、 ⇒ 0 + y = 600 ⇒ y = 600
y = 0とすると、 ⇒ 2x + 0 = 600 ⇒ x = 300
これで、点座標 Z = 3x + 4y が得られました。
| 頂点 | Z = 3x + 4y |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300,0) | Z = 3 × 300 + 4 × 0 = 900 |
| (150、300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0,450) | Z = 3 × 0 + 4 × 450 = 1800 |
したがって、最適解の最大値は、座標 x = 0 および y = 450 で Z = 1800 になります。グラフを以下に示します。

線形計画法の最新のアプリケーション
強力な数学的手法である線形計画法は、さまざまな業界で最適化問題を解決するために使用されています。以下に最新のアプリケーションをいくつか示します。
- サプライチェーンの最適化 : 線形計画法は、企業がサプライ チェーンのコストを最小限に抑え、効率を最大化するのに役立ちます。最もコスト効率の高い輸送ルート、倉庫業務、在庫管理戦略を決定するために使用されます。
- エネルギー管理 : エネルギー分野では、エネルギー生産方法の組み合わせを最適化するために線形計画法が利用されています。これには、需要を満たしながらコストと環境への影響を削減するために、従来のエネルギー源と再生可能エネルギー源のバランスを取ることが含まれます。
- 通信ネットワーク設計 : 線形計画法は、効率的な通信ネットワークの設計に役立ちます。帯域幅の割り当て、ネットワーク レイアウトの設計、データ フローの最適化に役立ち、低コストで高速通信を確保します。
- 財務計画 :企業や財務アナリストは、ポートフォリオの最適化、リスク管理、資本予算計画に線形計画法を使用します。リスクを最小限に抑えながら収益を最大化する投資決定を行うのに役立ちます。
- ヘルスケア物流 : ヘルスケアでは、線形計画法を適用して、病院のベッド、医療スタッフ、機器などのリソースの割り当てを最適化します。これは、患者ケアを改善し、待ち時間を短縮し、コストを効果的に管理するために非常に重要です。
- 製造プロセスの最適化 : 線形計画法は、労働力、材料、機械の可用性などの制約を考慮して、製造施設内の複数の製品の最適な生産レベルを決定するために使用されます。
- 農業計画 : 農家や農業プランナーは、線形計画法を使用して作物の選択、土地利用、資源の配分を決定し、資源を節約しながら収量と利益を最大化します。
- 航空会社の乗務員のスケジュール設定 : 航空会社は線形計画法を採用して乗務員を効率的にスケジュールし、規則に従ってフライトに人員を配置し、運航コストを最小限に抑えます。
これらのアプリケーションは、さまざまな分野にわたる複雑な最適化問題を解決する際の線形計画法の多用途性と威力を実証し、今日のデータ主導の世界における線形計画法の関連性を示しています。
オペレーションズ リサーチにおける線形計画法
- コアツール : 線形計画法は、リソースを最適化するためのオペレーションズ リサーチにおける基本的なツールです。
- 意思決定 : リソースの割り当て、利益の最大化、コストの最小化に関する最善の決定を下すのに役立ちます。
- 幅広い用途 :複雑な問題を解決するために、物流、製造、金融、医療などのさまざまな分野で使用されています。
- 現実世界の問題のモデル化 : 現実世界の問題を数学モデルに変換して、最も効率的な解決策を見つけます。
シンプレックス法
- 最適化アルゴリズム : シンプレックス法は、線形不等式に対する最適な解を見つけるために線形計画法で使用される強力なアルゴリズムです。
- 段階的なアプローチ : 制約によって定義された実行可能領域のエッジをナビゲートすることで、最適なソリューションに向かって繰り返し移動します。
- 効率 : 大規模な線形計画問題を解く効率が高いことで知られています。
- 多用途性 : 食事計画、ネットワーク フロー、生産スケジュールなどのさまざまな領域に適用でき、多用途性を示します。
線形計画法 – FAQ
線形計画法とは何ですか?
線形計画法は、さまざまな制約がある特定の線形問題を最適化するために使用される数学的概念です。線形計画法を使用して、与えられた問題の最適な出力を求めます。
線形計画問題とは何ですか?
線形計画問題 (LPP) は、与えられた条件に対して最適な解を与える問題です。
線形計画法とは何ですか?
一般的な線形計画法の公式は次のとおりです。
- 目的関数: Z = ax + by
- 制約: px + qy ≤ r、sx + ty ≤ u
- 非負の制限: x ≥ 0、y ≥ 0
線形計画法にはどのような種類がありますか?
さまざまな種類の線形計画法には次のものがあります。
- シンプレックス法による線形計画法
- R法による線形計画法
- グラフィカル手法による線形計画法
線形計画法の要件は何ですか?
線形計画問題のさまざまな要件は次のとおりです。
- 直線性
- 目的関数
- 制約
- 非否定性
線形計画法の利点は何ですか?
線形計画法にはさまざまな利点があります。
- あらゆる線形問題に対して最適な解決策を提供します。
- 使いやすく、常に一貫した結果が得られます
- 利益を最大化し、投入コストを削減するのに役立ちます。