7 セグメント表示の最小セグメント数

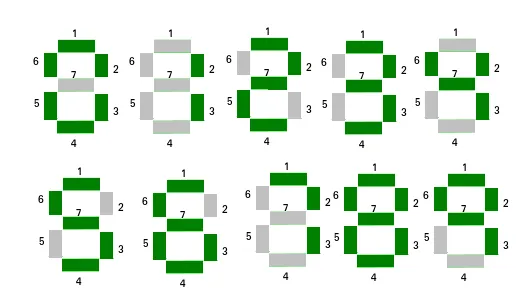
7セグメントディスプレイを使用して数字を表示できます。の配列が与えられると、 n 自然数。タスクは、数値を表示するために最小数のセグメントを使用する配列内の数値を見つけることです。複数の数値に最小数のセグメントがある場合は、最小のインデックスを持つ数値を出力します。

7セグメントディスプレイ' title=

例:

入力: arr[] = { 1 2 3 4 5 }。
出力: 1
説明： 最小数のセグメントを使用する要素は 1 (つまり 2 セグメント) です。
入力: arr[] = { 489 206 745 123 756 }。
出力: 745
説明： 最小数のセグメントを使用する最小のインデックスを持つ要素は 745 (つまり 12 セグメント) です。

このアイデアは、0 から 9 までの数字で使用されるセグメントの数を事前に計算して保存することです。次に、配列の各要素について、各桁で使用されるセグメントの数を合計します。次に、最小数のセグメントを使用している要素を見つけます。

桁ごとに使用されるセグメントの数:
0 -> 6
1 -> 2
2 -> 5
3 -> 5
4 -> 4
5 -> 5
6 -> 6
7 -> 3
8 -> 7
9 -> 6

C++

#include   using namespace std; // Precomputed values of segment used by digit 0 to 9. const int seg[10] = { 6 2 5 5 4 5 6 3 7 6}; // Return the number of segments used by x. int computeSegment(int x) {  if (x == 0)  return seg[0];  int count = 0;  // Finding sum of the segment used by  // each digit of a number.  while (x)  {  count += seg[x%10];  x /= 10;  }  return count; } int elementMinSegment(vector<int> arr int n) {  // Initialising the minimum segment and minimum  // number index.  int minseg = computeSegment(arr[0]);  int minindex = 0;  // Finding and comparing segment used  // by each number arr[i].  for (int i = 1; i < n; i++)  {  int temp = computeSegment(arr[i]);  // If arr[i] used less segment then update  // minimum segment and minimum number.  if (temp < minseg)  {  minseg = temp;  minindex = i;  }  }  return arr[minindex]; } int main() {  vector<int> arr = {489 206 745 123 756};  int n = arr.size();   cout << elementMinSegment(arr n) << endl;  return 0; }

Java

import java.io.*; class GFG {   // Precomputed values of segment  // used by digit 0 to 9. static int []seg = { 6 2 5 5 4 5 6 3 7 6}; // Return the number of segments used by x. static int computeSegment(int x) {  if (x == 0)  return seg[0];  int count = 0;  // Finding sum of the segment used by  // each digit of a number.  while (x > 0)  {  count += seg[x % 10];  x /= 10;  }  return count; } static int elementMinSegment(int []arr int n) {  // Initialising the minimum segment   // and minimum number index.  int minseg = computeSegment(arr[0]);  int minindex = 0;  // Finding and comparing segment used  // by each number arr[i].  for (int i = 1; i < n; i++)  {  int temp = computeSegment(arr[i]);  // If arr[i] used less segment then update  // minimum segment and minimum number.  if (temp < minseg)  {  minseg = temp;  minindex = i;  }  }  return arr[minindex]; }  static public void main (String[] args)  {  int []arr = {489 206 745 123 756};  int n = arr.length;  System.out.println(elementMinSegment(arr n));  } }

Python

# Precomputed values of segment # used by digit 0 to 9. seg = [6 2 5 5 4 5 6 3 7 6] # Return the number of # segments used by x. def computeSegment(x): if(x == 0): return seg[0] count = 0 # Finding sum of the segment  # used by each digit of a number. while(x): count += seg[x % 10] x = x // 10 return count # function to return minimum sum index def elementMinSegment(arr n): # Initialising the minimum  # segment and minimum number index. minseg = computeSegment(arr[0]) minindex = 0 # Finding and comparing segment # used by each number arr[i]. for i in range(1 n): temp = computeSegment(arr[i]) # If arr[i] used less segment # then update minimum segment # and minimum number. if(temp < minseg): minseg = temp minindex = i return arr[minindex] # Driver Code arr = [489 206 745 123 756] n = len(arr) # function print required answer print(elementMinSegment(arr n)) # This code is contributed by # Sanjit_Prasad

using System; class GFG{   // Precomputed values of segment // used by digit 0 to 9. static int []seg = new int[10]{ 6 2 5 5 4  5 6 3 7 6}; // Return the number of segments used by x. static int computeSegment(int x) {  if (x == 0)  return seg[0];  int count = 0;  // Finding sum of the segment used by  // each digit of a number.  while (x > 0)  {  count += seg[x % 10];  x /= 10;  }  return count; } static int elementMinSegment(int []arr int n) {  // Initialising the minimum segment  // and minimum number index.  int minseg = computeSegment(arr[0]);  int minindex = 0;  // Finding and comparing segment used  // by each number arr[i].  for (int i = 1; i < n; i++)  {  int temp = computeSegment(arr[i]);  // If arr[i] used less segment then update  // minimum segment and minimum number.  if (temp < minseg)  {  minseg = temp;  minindex = i;  }  }  return arr[minindex]; }  static public void Main()  {  int []arr = {489 206 745 123 756};  int n = arr.Length;  Console.WriteLine(elementMinSegment(arr n));  } }

JavaScript

// Precomputed values of segment // used by digit 0 to 9. let seg = [ 6 2 5 5 4 5 6 3 7 6]; // Return the number of segments used by x. function computeSegment(x) {  if (x == 0)  return seg[0];  let count = 0;  // Finding sum of the segment used by  // each digit of a number.  while (x > 0)  {  count += seg[x % 10];  x = parseInt(x / 10 10);  }  return count; } function elementMinSegment(arr n) {    // Initialising the minimum segment  // and minimum number index.  let minseg = computeSegment(arr[0]);  let minindex = 0;  // Finding and comparing segment used  // by each number arr[i].  for(let i = 1; i < n; i++)  {  let temp = computeSegment(arr[i]);  // If arr[i] used less segment then update  // minimum segment and minimum number.  if (temp < minseg)  {  minseg = temp;  minindex = i;  }  }  return arr[minindex]; } // Driver code let arr = [ 489 206 745 123 756 ]; let n = arr.length; console.log(elementMinSegment(arr n));

出力

時間計算量: O(n * log ₁₀ n)
補助スペース：O(10)

クイズの作成