ニュートンの冷却の法則は、物体が放射を介して周囲に伝達する熱の速度を記述する基本法則です。この法則は、温度差が小さい場合、物体が熱を放射する速度は周囲との温度差に直接比例すると述べています。つまり、物体の温度とその周囲の温度の差が大きいほど、より多くの熱が失われ、温度が低いほど、より多くの熱が失われます。ニュートンの冷却の法則は、ステファン ボルツマンの法則の特殊なケースです。
この記事では、ニュートンの冷却の法則、ニュートンの冷却の法則の公式、その導出、例などについて詳しく学びます。
ニュートンの冷却の法則の定義
ニュートン 彼は、物体から周囲へ失われる熱との関係を初めて研究した。彼は、物体とその周囲の温度差が大きければ大きいほど、物体から放射される熱も多くなると述べています。
ニュートンの冷却の法則 と述べています
温度差が大きくない場合、物体からの熱損失率は、物体とその周囲の温度の差に直接比例します。
この法則は、テーブルの上に残されたお湯や牛乳のほうが、テーブルの上に少し温かい牛乳や水が残った場合よりも早く冷める理由を説明するために使用されます。ニュートンの冷却の法則は、体の初期温度と周囲の温度を考慮して、実際に測定することなく人の体温を測定するのに役立ちます。
ニュートンの冷却の法則の公式
ニュートンの冷却の法則の公式は、材料が放射によって周囲に熱を失うときの材料の温度を計算するための公式です。
ニュートンの冷却の法則によれば、
熱の損失率 ( – dQ/dt) 体の温度は温度差に正比例します [ΔT = (T 2 – T 1 )] 身体も周囲も。
javaを設定する
次のように表すことができます。
– dQ/dt ∝ (T 2 – T 1 )
– dQ/dt = k(T 2 – T 1 )
どこ、
k は比例定数です
上記の微分方程式を解くと、次のようになります。
T(t) = T s + (T ○ – T s ) それは -kt
どこ、
t 時間です
T(t) 時間 t における身体の温度です。
T s 周囲の温度です
T ○ は体の初期温度です
k は比例定数です
ニュートンの冷却の法則の導出
ニュートンの冷却の法則の公式は、微分方程式の解を使用して導き出すことができます。比熱容量 s の質量 m の物体が温度 T にあるとします。2そしてT1周囲の温度です。
少しでも気温が下がったら dT 2 時間内に dt 、すると、失われる熱量は、
dQ = ミリ秒 dT 2
熱損失率は次式で与えられます。
dQ/dt = ms (dT 2 /dt)
ニュートンの冷却の法則によれば、
– dQ/dt = k(T 2 – T 1 )
上式を比較すると
– ミリ秒 (dT 2 /dt) = k (T 2 – T 1 )
dT 2 /(T 2 –T 1 ) = – (k / ミリ秒) dt
dT 2 /(T 2 – T 1 ) = – Kdt
どこ、 K = k/ms
上式を積分すると
ログ それは (T 2 – T 1 ) = – K t + c
T 2 = T 1 +C'と –Kt
取り消し線のマークダウンどこ、 C’ = e c
本体温度の低下と時間の関係を冷却グラフで示します。このグラフの傾きは温度の低下速度を示しています。
冷却曲線は、体温と時間の関係を示すグラフです。温度低下率は、任意の点における曲線の接線の傾きによって決まります。以下に追加した画像は、温度低下と時間の関係を示しています。
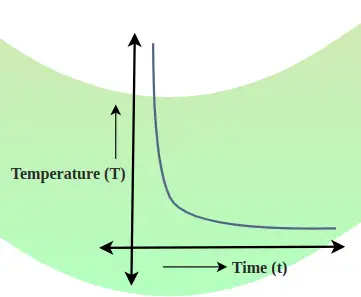
一般的に、
T(t) = T あ +(T H -T あ )そうです -kt
どこ
T(t) は時間 t における温度です
T あ 周囲温度または周囲の温度です
T H 熱い物体の温度です
k は正の定数、t は時間です
ニュートンの冷却の法則を適用する方法
一定の冷却速度では、冷却速度は間隔中の体の平均温度に関係し、ニュートンの冷却の法則を使用して近似値を計算できます。
dθ/dt = k(q – q s )
どこ、
q 体の温度です
q s 周囲の温度です
さて、体温の平均を q とすると、
q = (q 私 +q f )/2
ニュートンの冷却の法則の検証
ニュートンの冷却の法則は、以下に説明する実験によって簡単に検証できます。
実験では、2 つの壁の間に水が入った二重壁容器 (V) を使用します。二重壁容器の中に、熱水を入れた銅熱量計 (C) を入れます。
体温計は2本使っていますT2熱量計内の水の温度を測定し、T1温度を測る 二重壁の間に熱湯が入ります。等しい時間間隔の後、両方の温度が記録され、ログ間のグラフが表示されます。それは(T2–T1) と時間 (t) がプロットされ、負の傾きを持つ直線として表示されます。
ニュートンの冷却の法則グラフ
ニュートンの冷却の法則のグラフを以下に追加します。このグラフには、2 つの温度の差と時間の対数が表示されます。
ニュートンの冷却の法則の限界
ニュートンの冷却の法則にはさまざまな制限があります。
- ニュートンの冷却の法則は、身体と環境の温度差が小さい場合に当てはまります。
- 身体による熱の損失は形だけです。 放射線 。
- 身体が冷却されている間、周囲の温度は一定に保たれなければなりません。そうでない場合、ニュートンの冷却の法則は成り立ちません。
ニュートンの冷却の法則の応用
ニュートンの冷却の法則のさまざまな応用例は次のとおりです。
- 温かい物体が特定の温度まで冷却されるまでにかかる時間を推定します。
- 特定の時間が経過した後の冷蔵庫内の飲み物の温度を測定します。
- 死亡時の予想体温と現在の体温を調べることで、死亡時刻を知るのに役立ちます。
続きを読む、
- 比熱容量
- 熱力学の基本概念
- 熱力学プロセス
解決済みの例 ニュートンの冷却の法則
例 1: 室温が 20 °C の場合、熱い食品を入れた鍋は 2 分で 94 °C から 86 °C まで下がります。 71 °C から 69 °C に冷却するにはどのくらい時間がかかりますか?
解決:
94℃と86℃の平均は90℃、
- T2= 90 °C
- T1= 20 °C
チームにドロップインしてください。食品の温度は 2 分で 8 °C になります。
ニュートンの冷却の法則によれば、
– dQ/dt = k(T 2 –T 1 )
8 °C /2 分 = k(90 – 20)
4 = k(70) ……(1)
69 °C と 71 °C の平均は 70 °C
- T2= 70 °C
- T1= 20 °C
ニュートンの冷却の法則によれば、
2 °C /dt = k(70 – 20) ……(2)
式 (1) と (2) から、
時間の変化 = 0.7 分 = =42 秒
したがって、食品が 71 °C から 69 °C に冷却されるまでには 42 秒かかります。
例 2: 温度 40℃の物体を 20℃の恒温環境に置いた場合。 10分で温度が35℃まで下がるのが観察されます。体の温度が 30°C に達するまでにどれくらいの時間がかかるかを調べてください。
解決:
考えると、
- q私= (40 – 20)℃
- qf= (35 – 20)℃
ニュートンの冷却の法則によると
q f =q 私 それは -kt
次に、温度が 40 °C から 35 °C に下がる区間についてです。
(35 – 20) = (40 – 20) および-(10k)
それは-10k= 3/4
-10k = (ln 4/3)
ぎこちないメッシュグリッドk = 0.2876/10
k = 0.02876
ここで再び Newon の公式を使用して、
(30 – 20) = (35 – 20)e-kt
10 = 15e-kt
それは-kt= 23
-kt = ln(2/3)
t = 0.40546/k
k の値を使用すると、
t = 0.40546/0.02876
t = 14.098 分
したがって、体が 30℃の温度に達するまでにかかる時間は 14.098 分です。
例 3: 油を 70 °C に加熱します。 6分後に50℃まで冷却します。周囲温度 T を考慮して、オイルが 50 °C から 40 °C に冷却するのにかかる時間を計算します。 s = 25℃
解決:
考えると、
6 分後のオイルの温度、つまり T(t) は 50 °C に等しい
- 周囲温度 Ts= 25℃
- 油の温度、T○= 70℃
- 50℃まで冷却する時間 = 6 分
ニュートンの冷却の法則によれば、
Java intから文字列へT(t) = Ts+ (T0– Ts) それは-kt
{T(t) – Ts}/(T○– Ts) = そして-kt
-kt = ln[(T(t) – Ts)/(T○– Ts)] ……(1)
値を置き換えます
-kt = ln[(50 – 25)/(70 – 25)]
-k = (ln 0.55556)/6
k = 0.09796
50 °C から 40 °C までの平均温度は 45 °C に相当します
再びニュートンの冷却の法則を使用する
-(0.09796)t = ln[(45 – 25)/(70 – 25)]
-0.09796t = ln(0.44444)
0.09796t = 0.81093
t = 0.09796/0.58778 = 8.278分
したがって、油が 50 °C から 40 °C に冷えるのにかかる時間は、 8.278分
例 4: 水は 80 °C で 10 分間加熱されます。 k = 0.056/min、周囲の温度が 25 °C の場合、その温度は摂氏でいくらになりますか?
解決:
考えると、
- 周囲温度 Ts= 25℃
- 水の温度 T0= 80℃
- 水の加熱時間 (t) = 10 分
- 定数 k の値 = 0.056。
ニュートンの冷却の法則によれば、
T(t) = Ts+ (T0– Ts) それは-kt
値の置換
T(t)= 25 + (80 – 25)e-(0.056×10)
T(t) = 25 + 55 e-(0.056×10)
T(t) = 25 + 31.42
T(t) = 56.42
10分後、水の温度は次のようになります。 56.42℃。
ニュートンの冷却の法則に関するよくある質問
Q1: ニュートンの冷却の法則とは何ですか?
答え:
ニュートンの冷却の法則では、物体による熱損失率は、物体とその周囲の温度の差に正比例すると述べています。
Q2: ニュートンの冷却の法則とは何ですか?
答え:
スプリング ブートの注釈
ニュートンの冷却の法則によると、次のようになります。
T(t) = T s + (T ○ – T s ) それは -kt
Q3: ニュートンの冷却の法則の k とは何ですか?
答え:
の k ニュートンの冷却の法則の公式における は、材料に依存する定数です。つまり、材料を変更すると、 k ニュートンの冷却の法則で。
Q4: ホットミルクはなぜグラスよりボウルの方が飲みやすいのですか?
答え:
ボウルはガラスよりも表面積が大きいため、ボウルを介した熱放射の形でより多くの熱が周囲に失われるため、ボウルからホットミルクを飲みやすくなります。
