コンピューターサイエンスには、解決策がまだ見つかっていない問題がいくつか存在し、問題は次のようなクラスに分類されます。 複雑さのクラス 。複雑性理論では、複雑性クラスは、関連する複雑性を持つ問題のセットです。これらのクラスは、科学者が問題を解決し、解決策を検証するために必要な時間とスペースに基づいて問題をグループ化するのに役立ちます。これは、問題を解決するために必要なリソースを扱う計算理論の一分野です。
Javaメソッドが含まれています
一般的なリソースは時間と空間です。これは、アルゴリズムが問題を解決するのにかかる時間と、それに対応するメモリ使用量を意味します。
- アルゴリズムの時間計算量は、問題を解決するために必要なステップ数を表すために使用されますが、答えを検証するのにかかる時間を表すためにも使用できます。
- アルゴリズムの空間複雑度は、アルゴリズムが動作するために必要なメモリの量を表します。
複雑さのクラスは、同様の種類の問題を整理するのに役立ちます。
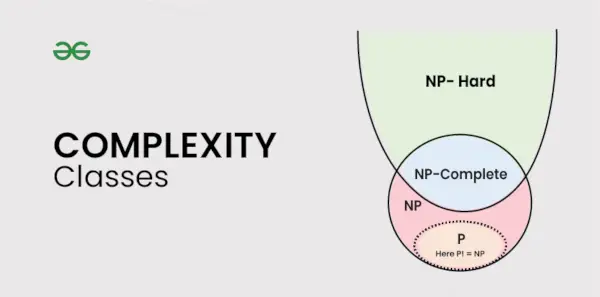
複雑さのクラスの種類
この記事では、次の複雑さのクラスについて説明します。
- Pクラス
- NPクラス
- CoNPクラス
- NPハード
- NP完全
Pクラス
PクラスのPは 多項式時間。 これは、決定論的マシンによって多項式時間で解くことができる決定問題 (はいまたはいいえで答えられる問題) の集合です。
特徴:
- 解決策 P問題 を見つけるのは簡単です。
- P 多くの場合、これは解決可能で扱いやすい計算問題の一種です。扱いやすいとは、問題が理論的にも実践的にも解決できることを意味します。しかし、理論的には解決できても実際には解決できない問題は、難解決として知られています。
このクラスには多くの問題が含まれています。
- 最大公約数を計算します。
- 最大一致を見つける。
- マージソート
NPクラス
NPクラスのNPとは、 非決定的な多項式時間 。これは、非決定論的なマシンによって多項式時間で解決できる決定問題の集合です。
JavaScript文字列置換
特徴:
- NP クラスの解は非決定論的なマシンによって解かれるため、見つけるのは困難ですが、解を検証するのは簡単です。
- NP の問題は、チューリング マシンによって多項式時間で検証できます。
例:
をよりよく理解するために例を考えてみましょう NPクラス 。合計を持っている会社があるとします。 1000 ユニークな従業員を持つ従業員 ID 。あると仮定します 200 彼らが利用できる部屋。厳選された 200 従業員はペアになる必要がありますが、会社の CEO は、個人的な理由により同じ部屋で働くことができない従業員のデータを持っています。
これは一例です 例えば 問題。与えられた選択肢が正しいかどうかを確認するのは簡単なので、 200 同僚によって提案された従業員が満足できるかどうか、つまり、同僚リストから選択されたペアが CEO によって与えられたリストに表示されません。しかし、そのようなリストを最初から作成するのは非常に困難であるため、完全に非現実的であると思われます。
これは、誰かが問題の解決策を提供してくれれば、多項式時間で正しいペアと誤ったペアを見つけることができることを示しています。したがって、 例えば クラスの問題であれば、多項式時間で計算できる答えが可能です。
このクラスには、効果的に解決できるようにしたい多くの問題が含まれています。
- ブール充足可能性問題 (SAT)。
- ハミルトニアンパス問題。
- グラフの色付け。
共同NPクラス
Co-NP は NP クラスの補完を表します。これは、Co-NP の問題に対する答えが「いいえ」の場合、多項式時間でチェックできる証明があることを意味します。
特徴:
- 問題 X が NP にある場合、その補数 X’ も CoNP にあります。
- NP および CoNP 問題の場合、多項式時間ですべての答えを一度に検証する必要はありません。問題が NP または CoNP であるかどうかについては、多項式時間で 1 つの特定の答え (はいまたはいいえ) だけを検証する必要があります。
CoNP の問題の例は次のとおりです。
- 素数を調べるため。
- 整数因数分解。
NPハードクラス
NP 困難な問題は、NP の最も難しい問題と少なくとも同じくらい難しく、NP のすべての問題が NP 困難に帰着するような問題のクラスです。
特徴:
- すべての NP 困難な問題は NP にはありません。
- それらをチェックするには時間がかかります。これは、NP 困難問題の解が与えられた場合、それが正しいかどうかを確認するのに長い時間がかかることを意味します。
- NP 内のすべての問題 L に対して、L から A への多項式時間短縮が存在する場合、問題 A は NP 困難です。
Np-hard の問題の例としては、次のようなものがあります。
25/100
- 停止問題。
- 修飾されたブール式。
- ハミルトニアンサイクルはありません。
NP完全クラス
問題が NP と NP 困難の両方である場合、問題は NP 完全です。 NP 完全問題は、NP の難しい問題です。
特徴:
- NP 完全問題は、NP クラスの問題を多項式時間で NP 完全問題に変換または還元できるため、特別です。
- NP 完全問題を多項式時間で解くことができれば、あらゆる NP 問題も多項式時間で解くことができます。
問題の例としては次のようなものがあります。
- ハミルトニアンサイクル。
- 満足度。
- 頂点カバー 。
| 複雑さのクラス | 特徴的な機能 |
| P | 多項式時間で簡単に解けます。 |
| 例えば | はい、答えは多項式時間でチェックできます。 |
| 共同NP | いいえ、答えは多項式時間で確認できます。 |
| NPハード | NP 困難な問題はすべて NP に含まれていないため、確認するのに時間がかかります。 |
| NP完全 | NP および NP が難しい問題は、NP 完全です。 |
