坂道とは何ですか?
線が正しいかどうかを表す絶対値の数。 より急な、またはより平らな そしてその 方向 グラフ上の線は、 斜面または勾配。 線の傾きは経済学と数学の基本的な概念です。一般的には文字で表されます 「ん」。 傾きは次のように割ることで計算できます。 「垂直方向の変化」 とともに 「水平方向の変化」 直線上の 2 つの異なる点の間。
坂道の種類
斜面には主に次の 2 つのタイプがあります。
グラフィック用語では、正の傾きとは、グラフ上の線が左から右に移動するときに上昇することを指します。正の傾きの概念は、次の助けを借りて明確に理解できます。 供給曲線 経済学のプロデューサーまたは企業の。曲線の 2 つの変数は、Y 軸の価格と X 軸の商品数量です。その企業が次の商品を生産していると仮定しましょう。 利益の最大化。 したがって、財の価格が上昇すると、企業が供給する財の量も増加し、価格が下落すると、企業が供給する量は減少します。言い換えれば、企業または生産者は、価格が高くなると、より多くの利益を得るために供給量を増やし、価格が安くなると、損失を減らすために供給量を減らします。したがって、価格と供給量が互いに正の相関関係にあることは、以下の図からも明らかです。
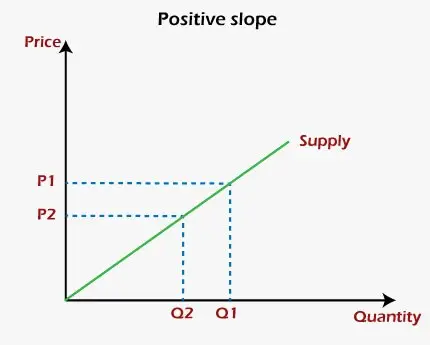
グラフ上で言うと、負の傾きとは、グラフ上の線が左から右に移動するときに傾く傾きを指します。グラフの負の傾きの最も良い例の 1 つは、 需要曲線 経済学で。曲線の 2 つの変数は、Y 軸の価格と X 軸の商品数量です。ご存知のとおり、消費者は高い価格よりも低い価格で商品を大量に購入します。したがって、消費者が求める商品の量は、商品の価格が上昇すると減少します。逆に、商品の価格が下がると、需要量が増加します。したがって、それは、 負の関係 それらの商品の価格と供給量との間の関係。それは以下の図から明らかです。

他の 2 種類の坂道
正と負の勾配の他に、ゼロ勾配と無限勾配という名前のさらに 2 種類の勾配があります。それらは与えられた説明から理解できます。
以下の図は、ゼロ勾配をグラフで表したものです。

無限の傾きが次の図に示されています。

傾きの計算
- 次の線形方程式では、 ax + by + c = 0、 傾きは次のように定義されます -a/b。
- 直線の方程式は、次の助けを借りて計算できます。 点と傾きの公式 両方の斜面の場合 メートル 線と点の (x1、y1) が知られています。式は次のとおりです。
y - y1 = m (x - x1) - 2行は次のようになります 平行 それらの傾斜が 等しい、 一方、2行は 垂直 それらの傾きの積が -1.
追加情報
- 傾きの絶対値は、曲線が正しいかどうかを調べるために使用されます。 より急な、またはより平坦な。
- 傾きの正と負の値によって方向が決まります。つまり、 上向きか下向きか、 斜面の。
- 曲線になる より急な 傾きの絶対値が増加します。
- 曲線になる お世辞 傾きの絶対値が減少します。
- これらの条件は、 負または正の傾き (負または正の値ではありません)。
- あ より低い正の傾き 上方向に傾斜したより平坦な曲線が形成されることを意味します。
- あ より高い正の傾き 上方向に曲がるより急な曲線が形成されることを意味します。
- あ 絶対値が大きい負の傾き 下方向に傾斜するより急な曲線が形成されることを意味します。
- あ 絶対値が小さい負の傾き は、下方向に曲がったより平らな曲線が形成されることを意味します。
