前提条件: 線形回帰
線形回帰は、教師あり学習に基づいた機械学習アルゴリズムです。回帰タスクを実行します。回帰は、独立変数に基づいてターゲット予測値をモデル化します。主に、変数と予測の間の関係を調べるために使用されます。異なる回帰モデルは、考慮している従属変数と独立変数の間の関係の種類、および使用される独立変数の数に基づいて異なります。この記事では、さまざまな Python ライブラリを使用して、特定のデータセットに線形回帰を実装する方法を説明します。視覚化しやすいため、バイナリ線形モデルを示します。このデモでは、モデルは勾配降下法を使用して学習します。ここでそれについて学ぶことができます。
ステップ1: 必要なライブラリをすべてインポートする
Python3
挿入ソートJava
import> numpy as np> import> pandas as pd> import> seaborn as sns> import> matplotlib.pyplot as plt> from> sklearn>import> preprocessing, svm> from> sklearn.model_selection>import> train_test_split> from> sklearn.linear_model>import> LinearRegression> |
>
>
ステップ2: データセットの読み取り:
Python3
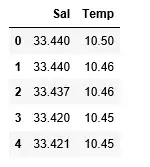
df>=> pd.read_csv(>'bottle.csv'>)> df_binary>=> df[[>'Salnty'>,>'T_degC'>]]> > # Taking only the selected two attributes from the dataset> df_binary.columns>=> [>'Sal'>,>'Temp'>]> #display the first 5 rows> df_binary.head()> |
>
>
出力:
ステップ 3: データの分散を調査する
Python3
#plotting the Scatter plot to check relationship between Sal and Temp> sns.lmplot(x>=>'Sal'>, y>=>'Temp'>, data>=> df_binary, order>=> 2>, ci>=> None>)> plt.show()> |
>
>
出力:

ステップ 4: データクリーニング
Python3
# Eliminating NaN or missing input numbers> df_binary.fillna(method>=>'ffill'>, inplace>=> True>)> |
>
>
ステップ5: モデルをトレーニングする
Python3
それ以外の場合 Java
X>=> np.array(df_binary[>'Sal'>]).reshape(>->1>,>1>)> y>=> np.array(df_binary[>'Temp'>]).reshape(>->1>,>1>)> > # Separating the data into independent and dependent variables> # Converting each dataframe into a numpy array> # since each dataframe contains only one column> df_binary.dropna(inplace>=> True>)> > # Dropping any rows with Nan values> X_train, X_test, y_train, y_test>=> train_test_split(X, y, test_size>=> 0.25>)> > # Splitting the data into training and testing data> regr>=> LinearRegression()> > regr.fit(X_train, y_train)> print>(regr.score(X_test, y_test))> |
>
>
出力:

ステップ6: 結果を調べる
Python3
ロム
y_pred>=> regr.predict(X_test)> plt.scatter(X_test, y_test, color>=>'b'>)> plt.plot(X_test, y_pred, color>=>'k'>)> > plt.show()> # Data scatter of predicted values> |
>
>
出力:

モデルの精度スコアが低いことは、回帰モデルが既存のデータにあまり適合していないことを示唆しています。これは、私たちのデータが線形回帰に適していないことを示唆しています。ただし、データセットの一部のみを考慮すると、データセットが線形回帰変数を受け入れる場合があります。その可能性を検証してみましょう。
ステップ 7: より小さなデータセットの操作
Python3
df_binary500>=> df_binary[:][:>500>]> > # Selecting the 1st 500 rows of the data> sns.lmplot(x>=>'Sal'>, y>=>'Temp'>, data>=> df_binary500,> >order>=> 2>, ci>=> None>)> |
>
>
出力:

最初の 500 行が線形モデルに従っていることはすでにわかります。前と同じ手順を続けます。
Python3
math.random Java
df_binary500.fillna(method>=>'fill'>, inplace>=> True>)> > X>=> np.array(df_binary500[>'Sal'>]).reshape(>->1>,>1>)> y>=> np.array(df_binary500[>'Temp'>]).reshape(>->1>,>1>)> > df_binary500.dropna(inplace>=> True>)> X_train, X_test, y_train, y_test>=> train_test_split(X, y, test_size>=> 0.25>)> > regr>=> LinearRegression()> regr.fit(X_train, y_train)> print>(regr.score(X_test, y_test))> |
>
>
出力:

Python3
y_pred>=> regr.predict(X_test)> plt.scatter(X_test, y_test, color>=>'b'>)> plt.plot(X_test, y_pred, color>=>'k'>)> > plt.show()> |
>
>
出力:

ステップ8: 回帰の評価指標
最後に、評価指標を利用して線形回帰モデルのパフォーマンスをチェックします。回帰アルゴリズムでは、モデルのパフォーマンスをチェックするためにmean_absolute_errorおよびmean_squared_errorメトリクスを広く使用しています。
Python3
from> sklearn.metrics>import> mean_absolute_error,mean_squared_error> > mae>=> mean_absolute_error(y_true>=>y_test,y_pred>=>y_pred)> #squared True returns MSE value, False returns RMSE value.> mse>=> mean_squared_error(y_true>=>y_test,y_pred>=>y_pred)>#default=True> rmse>=> mean_squared_error(y_true>=>y_test,y_pred>=>y_pred,squared>=>False>)> > print>(>'MAE:'>,mae)> print>(>'MSE:'>,mse)> print>(>'RMSE:'>,rmse)> |
>
>
出力:
MAE: 0.7927322046360309 MSE: 1.0251137190180517 RMSE: 1.0124789968281078>
