ランダム フォレストは、教師あり学習手法に属する人気のある機械学習アルゴリズムです。これは、ML の分類問題と回帰問題の両方に使用できます。というコンセプトに基づいています。 アンサンブル学習、 それは次のプロセスです 複数の分類器を組み合わせて複雑な問題を解決し、モデルのパフォーマンスを向上させます。
その名の通り、 「ランダム フォレストは、特定のデータセットのさまざまなサブセットに関する多数のデシジョン ツリーを含み、平均を取ることでそのデータセットの予測精度を向上させる分類器です。」 ランダム フォレストは、1 つの決定ツリーに依存するのではなく、各ツリーから予測を取得し、予測の多数決に基づいて最終出力を予測します。
フォレスト内の木の数が多いほど精度が向上し、過剰適合の問題が防止されます。
インラインスタイルに反応する
以下の図は、ランダム フォレスト アルゴリズムの仕組みを説明しています。
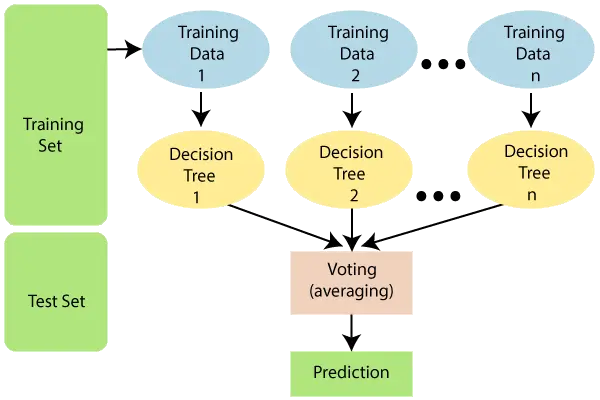
注: ランダム フォレスト アルゴリズムをより深く理解するには、デシジョン ツリー アルゴリズムについての知識が必要です。
ランダム フォレストの前提条件
ランダム フォレストは複数のツリーを組み合わせてデータセットのクラスを予測するため、一部のデシジョン ツリーは正しい出力を予測する可能性がありますが、他のデシジョン ツリーは予測できない可能性があります。しかし、すべてのツリーが一緒になって、正しい出力を予測します。したがって、より優れたランダム フォレスト分類器のための 2 つの仮定を以下に示します。
- 分類器が推測された結果ではなく正確な結果を予測できるように、データセットの特徴変数に実際の値がいくつか存在する必要があります。
- 各ツリーからの予測の相関は非常に低いはずです。
ランダム フォレストを使用する理由
以下は、ランダム フォレスト アルゴリズムを使用する必要がある理由を説明するいくつかのポイントです。
- 他のアルゴリズムと比較して、トレーニングにかかる時間が短くなります。
- 大規模なデータセットであっても効率的に実行され、高精度で出力を予測します。
- データの大部分が欠落している場合でも精度を維持できます。
ランダムフォレストアルゴリズムはどのように機能しますか?
ランダム フォレストは 2 つのフェーズで動作します。1 つは N 個の決定木を組み合わせてランダム フォレストを作成することで、2 つ目は、最初のフェーズで作成された各ツリーに対して予測を行うことです。
作業プロセスは、以下の手順と図で説明できます。
ステップ1: トレーニング セットからランダムな K データ ポイントを選択します。
ステップ2: 選択したデータ ポイント (サブセット) に関連付けられたデシジョン ツリーを構築します。
ステップ-3: 構築するデシジョン ツリーの数 N を選択します。
一般保護違反
ステップ-4: ステップ 1 と 2 を繰り返します。
ステップ-5: 新しいデータ ポイントについては、各決定木の予測を見つけて、多数決を獲得したカテゴリに新しいデータ ポイントを割り当てます。
アルゴリズムの動作は、以下の例でよりよく理解できます。
例: 複数の果物の画像を含むデータセットがあるとします。したがって、このデータセットはランダム フォレスト分類器に与えられます。データセットはサブセットに分割され、各決定木に与えられます。トレーニング フェーズでは、各デシジョン ツリーが予測結果を生成し、新しいデータ ポイントが発生すると、結果の大部分に基づいて、ランダム フォレスト分類器が最終的な決定を予測します。以下の画像を考えてみましょう。

ランダムフォレストの応用
ランダム フォレストが主に使用されるセクターは主に 4 つあります。
ランダムフォレストのメリット
- ランダム フォレストは、分類タスクと回帰タスクの両方を実行できます。
- 高次元の大規模なデータセットを処理できます。
- これにより、モデルの精度が向上し、オーバーフィッティングの問題が防止されます。
ランダムフォレストのデメリット
- ランダム フォレストは分類タスクと回帰タスクの両方に使用できますが、回帰タスクにはあまり適していません。
ランダム フォレスト アルゴリズムの Python 実装
次に、Python を使用してランダム フォレスト アルゴリズム ツリーを実装します。このために、以前の分類モデルで使用したのと同じデータセット「user_data.csv」を使用します。同じデータセットを使用することで、ランダム フォレスト分類子を次のような他の分類モデルと比較できます。 デシジョンツリー分類器、 KNN、 SVM、ロジスティック回帰など
mysqlはすべてのユーザーを表示します
実装手順は以下のとおりです。
- データの前処理ステップ
- ランダム フォレスト アルゴリズムをトレーニング セットに適合させる
- テスト結果を予測する
- 結果のテスト精度(混同行列の作成)
- テストセットの結果を視覚化します。
1.データの前処理ステップ:
以下は前処理ステップのコードです。
# importing libraries import numpy as nm import matplotlib.pyplot as mtp import pandas as pd #importing datasets data_set= pd.read_csv('user_data.csv') #Extracting Independent and dependent Variable x= data_set.iloc[:, [2,3]].values y= data_set.iloc[:, 4].values # Splitting the dataset into training and test set. from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test= train_test_split(x, y, test_size= 0.25, random_state=0) #feature Scaling from sklearn.preprocessing import StandardScaler st_x= StandardScaler() x_train= st_x.fit_transform(x_train) x_test= st_x.transform(x_test)
上記のコードでは、データを前処理しました。データセットをロードした場所は次のようになります。

2. ランダム フォレスト アルゴリズムをトレーニング セットに適合させる:
次に、ランダム フォレスト アルゴリズムをトレーニング セットに適合させます。これに合わせるために、 RandomForestClassifier からのクラス スクラーンアンサンブル 図書館。コードを以下に示します。
#Fitting Decision Tree classifier to the training set from sklearn.ensemble import RandomForestClassifier classifier= RandomForestClassifier(n_estimators= 10, criterion='entropy') classifier.fit(x_train, y_train)
上記のコードでは、分類子オブジェクトは以下のパラメーターを受け取ります。
出力:
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='entropy', max_depth=None, max_features='auto', max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=1, min_samples_split=2, min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=None, oob_score=False, random_state=None, verbose=0, warm_start=False)
3. テストセットの結果の予測
モデルがトレーニング セットに適合しているため、テスト結果を予測できるようになりました。予測のために、新しい予測ベクトル y_pred を作成します。以下はそのコードです。
#Predicting the test set result y_pred= classifier.predict(x_test)
出力:
予測ベクトルは次のように与えられます。
C# サンプルコード

上記の予測ベクトルとテスト セットの実数ベクトルをチェックすることで、分類器によって行われた誤った予測を判断できます。
4. 混同行列の作成
次に、混同行列を作成して、正しい予測と誤った予測を決定します。以下はそのコードです。
#Creating the Confusion matrix from sklearn.metrics import confusion_matrix cm= confusion_matrix(y_test, y_pred)
出力:

上記のマトリックスからわかるように、次のものがあります。 4+4= 8 つの間違った予測 そして 64+28= 92 件の正しい予測。
5. トレーニングセットの結果を視覚化する
ここでは、トレーニング セットの結果を視覚化します。トレーニング セットの結果を視覚化するために、ランダム フォレスト分類器のグラフをプロットします。分類子は、ロジスティック回帰で行ったように、SUV 車を購入したユーザーまたは購入しなかったユーザーについて「はい」または「いいえ」を予測します。以下はそのコードです。
Javaでリストを並べ替える
from matplotlib.colors import ListedColormap x_set, y_set = x_train, y_train x1, x2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step =0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(x1, x2, classifier.predict(nm.array([x1.ravel(), x2.ravel()]).T).reshape(x1.shape), alpha = 0.75, cmap = ListedColormap(('purple','green' ))) mtp.xlim(x1.min(), x1.max()) mtp.ylim(x2.min(), x2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Random Forest Algorithm (Training set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show()
出力:

上の画像は、トレーニング セットの結果を操作するランダム フォレスト分類器の視覚化結果です。これは、デシジョン ツリー分類子と非常によく似ています。各データ ポイントは user_data の各ユーザーに対応し、紫と緑の領域が予測領域です。紫色の領域は SUV 車を購入しなかったユーザー用に分類され、緑色の領域は SUV を購入したユーザー用に分類されます。
したがって、ランダム フォレスト分類器では、購入済み変数に対して Yes または NO を予測した 10 個のツリーを取得しました。分類子は予測の大部分を取得して結果を提供しました。
6. テストセットの結果の視覚化
次に、テスト セットの結果を視覚化します。以下はそのコードです。
#Visulaizing the test set result from matplotlib.colors import ListedColormap x_set, y_set = x_test, y_test x1, x2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step =0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(x1, x2, classifier.predict(nm.array([x1.ravel(), x2.ravel()]).T).reshape(x1.shape), alpha = 0.75, cmap = ListedColormap(('purple','green' ))) mtp.xlim(x1.min(), x1.max()) mtp.ylim(x2.min(), x2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Random Forest Algorithm(Test set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show()
出力:

上の画像は、テスト セットの視覚化結果です。過剰適合の問題が発生することなく、誤った予測の最小数 (8) があることを確認できます。分類器内のツリーの数を変更すると、異なる結果が得られます。
