再帰関数は、それ自体を直接または間接的に呼び出すルーチンとして定義できます。
言い換えれば、再帰関数は、同じ問題の小さなインスタンスを解決することによって問題を解決する関数です。この手法は、より単純で類似したサブ問題に分解できる問題を解決するために、プログラミングで一般的に使用されます。
再帰関数の必要性:
再帰関数は、同じ問題の小さなインスタンスを解決することによって問題を解決する関数です。この手法は、より単純な同様のサブ問題に分解できる問題を解決するためにプログラミングでよく使用されます。
1. 複雑なタスクを解決する:
再帰関数は、複雑な問題を同じ問題の小さなインスタンスに分割し、コンパクトで読みやすいコードを生成します。
2. 分割して征服する:
再帰関数は、マージ ソートやクイックソートなどの分割統治アルゴリズムに適しており、問題を小さなサブ問題に分割し、再帰的に解決し、解決策を元の問題とマージします。
3. 後戻り :
再帰的バックトラッキングは、N-Queen や Sudoku などの問題を調査して解決するのに最適です。
4. ダイナミック プログラミング:
再帰関数は、部分問題を解決し、その解を完全な解に結合することにより、動的プログラミングの問題を効率的に解決します。
5. 木と グラフ構造:
再帰関数はツリー構造やグラフ構造の操作に最適で、トラバーサルやパターン認識タスクを簡素化します。 。
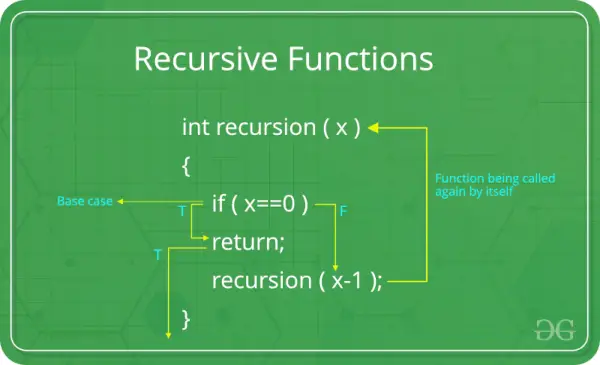
再帰関数の書き方:
再帰関数のコンポーネント:
規範事例: すべての再帰関数には基本ケースが必要です。基本ケースは、それ以上の再帰を必要としない最も単純なシナリオです。これは、関数がそれ自体を無期限に呼び出すことを防ぐ終了条件です。適切な基本ケースがないと、再帰関数は無限再帰につながる可能性があります。
再帰的な場合: 再帰的な場合、関数は変更された引数を使用してそれ自体を呼び出します。これが再帰の本質です。同じ問題の小さなインスタンスに分割することで、より大きな問題を解決します。再帰的なケースは、反復ごとに基本ケースに近づく必要があります。
の例を考えてみましょう 数値の階乗 :
この例では、基本的なケースは次のような場合です。 n は 0 、そして関数は戻ります 1 。再帰的な場合は倍増します n パラメータを指定して呼び出された関数の結果 n – 1 。このプロセスは、基本ケースに到達するまで継続されます。
再帰関数が正しい基本ケースを持ち、再帰呼び出しが基本ケースにつながることを確認することが重要です。そうしないと、プロシージャが無限に実行され、スタック オーバーフロー (関数呼び出しに割り当てられた利用可能なメモリを超える) が発生する可能性があります。
以下は、数値の階乗の実装です。
C++ #include using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) { // Base case if (n == 0) { return 1; } // Recursive case return n * factorial(n - 1); } // Driver Code int main() { int n = 4; cout << 'Factorial of ' << n << ' is:' << factorial(n); return 0; }> ジャワ import java.util.Scanner; public class Factorial { // Recursive Function to calculate the factorial of a number static int factorial(int n) { // Base case: If n is 0, the factorial is 1. if (n == 0) { return 1; } // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1). return n * factorial(n - 1); } public static void main(String[] args) { int n = 4; // Calculate and print the factorial of n. int result = factorial(n); System.out.println('Factorial of ' + n + ' is: ' + result); } }> パイソン # Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))> C# using System; class Program { // Recursive Function to calculate Factorial of a number static int Factorial(int n) { // Base case if (n == 0) { return 1; } // Recursive case return n * Factorial(n - 1); } // Driver Code static void Main() { int n = 4; Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n)); } }> JavaScript // Function to calculate the factorial of a number using recursion function factorial(n) { // Base case: If n is 0, the factorial is 1. if (n === 0) { return 1; } // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1). return n * factorial(n - 1); } // Main function function main() { // Given number let n = 4; // Calculate the factorial of n. let result = factorial(n); // Print the result console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();> 出力
Factorial of 4 is:24>
時間計算量: の上)
補助スペース: の上)
