三角法の Sin Cos 公式: 三角法はその名前が示すように、三角形の研究です。これは、直角三角形の辺の長さと角度の関係を研究する数学の重要な分野であり、三角形の不足している辺の長さや角度を決定するのにも役立ちます。三角比または関数には、サイン、コサイン、タンジェント、コセカント、セカント、コタンジェントの 6 つがあります。コセカント、セカント、コタンジェントは、それぞれ他の 3 つの関数、つまりサイン、コサイン、タンジェントの逆関数です。
三角比は、直角三角形の辺の長さの比として定義されます。三角法は私たちの日常生活のさまざまな分野で活用されています。丘や建物の高さを判断するのに役立ちます。犯罪学、建設、物理学、考古学、船舶エンジン工学などの分野でも使用されています。
この記事では、すべてを調査します 三角法の公式のほとんどは、sin と cos の公式とその例、および三角法のすべての公式のリストです。
目次
三角法の公式
∠Y = 90°である直角三角形 XYZ を考えます。頂点 Z での角度を θ とします。 θに隣接する側を隣接側、θと反対側を反対側と呼びます。斜辺は、直角の反対側の辺、または直角の最長の辺です。
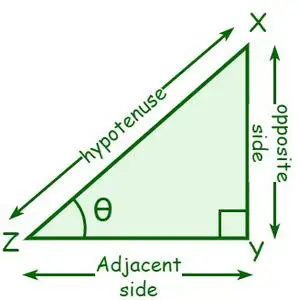
- sinθ = 対辺/斜辺
- cosθ = 隣辺/斜辺
- Tanθ = 反対側/隣接側
- cosec θ = 1/sin θ = 斜辺/反対側
- secθ=1/cosθ=斜辺/隣接辺
- cotθ = 1/tanθ = 隣接面/反対側
正弦の公式
直角三角形の角度の正弦は、指定された角度に対する対辺の長さと斜辺の長さの比です。正弦関数は sin として表されます。
sinθ = 対辺/斜辺
コサインの公式
直角三角形の角度の余弦は、指定された角度に対する隣接する辺の長さと斜辺の長さの比です。コサイン関数は cos で表されます。
CSSで画像を整列させるcosθ = 隣辺/斜辺
いくつかの基本的な Sin Cos 公式
象限のサイン関数とコサイン関数
- サイン関数は、第 1 象限と第 2 象限では正となり、第 3 象限と第 4 象限では負になります。
- コサイン関数は、第 1 象限と第 4 象限では正となり、第 2 象限と第 3 象限では負になります。
度
四分円
正弦関数の符号
コサイン関数の符号
0°~90°
第 1 象限
+(プラス)
+(プラス)
90°~180°
第2象限
+(プラス)
- (ネガティブ)
180°~270°
第3象限
- (ネガティブ)
- (ネガティブ)
270°~360°
第4象限
- (ネガティブ)
+(プラス)
サイン関数とコサイン関数の負の角度の恒等式
- 負の角度の正弦は常にその角度の負の正弦と等しくなります。
sin (-θ) = – sin θ
- 負の角度の余弦は常にその角度の余弦と等しくなります。
cos (-θ) = cosθ
サイン関数とコサイン関数の関係
sinθ = cos (90° – θ)
サイン関数とコサイン関数の逆関数
- コセカント関数は、サイン関数の逆関数です。
cosec θ = 1/sin θ
- セカント関数はコサイン関数の逆関数です。
secθ = 1/cosθ
ピタゴラス的アイデンティティ
それなし 2 θ+cos 2 θ = 1
サイン関数とコサイン関数の周期恒等式
sin (θ + 2nπ) = sin θ
cos (θ + 2nπ) = cos θ
サイン関数とコサイン関数の倍角公式
sin 2θ = 2 sin θ cos θ
cos 2θ = cos 2 θ – 罪 2 θ = 2cos 2 θ – 1 = 1 – 2 sin 2 私
サイン関数とコサイン関数の半角の恒等式
sin (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
サイン関数とコサイン関数の三重角恒等式
sin 3θ = 3 sinθ – 4 sin 3 私
cos 3θ = 4cos 3 θ – 3 cos θ
和と差の公式
- 正弦関数
sin (A + B) = sin A cos B + cos A sin B
sin (A – B) = sin A cos B – cos A sin B
- コサイン関数
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
サインの法則またはサインルール
サインの法則は、三角形の辺の長さと角度の関係を与える三角法則です。

a/sin A = b/sin B = c/sin C
ここで、a、b、c は三角形 ABC の 3 辺の長さ、A、B、C は角度です。
余弦の法則
余弦定理の余弦定理は、三角形の欠落または未知の角度または辺の長さを決定するために使用されます。

ある 2 = b 2 +c 2 – 2bc cos A
b 2 = c 2 +a 2 – 2ca cos B
c 2 = a 2 +b 2 – 2ab cos C
ここで、a、b、c は三角形 ABC の 3 辺の長さ、A、B、C は角度です。
Sin Cos の公式テーブル
以下は、度およびラジアンで表したさまざまな角度の Sin と Cos の公式表/リストです。
Sin Cos の公式リスト
| 角度 (度単位) | 角度 (ラジアン単位) | 私は罪を犯します | cosθ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | p/6 | 1/2 | _3/2 |
| 45° | p/4 | 1/√2 | 1/√2 |
| 60° | p/3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2人/3人 | √3/2 | -1/2 選択範囲の並べ替え |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° | 円周率 | 0 | -1 |
Sin Cos の公式の例
問題 1: cos α = 24/25 の場合、sin α の値を求めます。
解決:
考えると、
cosα = 24/25
私たちが持っているピタゴラス的アイデンティティから。
コス2θ+sin2θ = 1
(24/25)2+なし2α = 1
それなし2α = 1 – (24/25)2
それなし2α = 1 – (576/625) = (625 – 576)/625
それなし2α = (625 – 576)/625 = 49/626
sin α = √49/625 = ±7/25
したがって、sin α = ±7/25 となります。
問題 2: ∠A= 30°の場合の sin 2A と cos 2A の公式を証明してください。
解決:
とすると、∠A= 30°
私達はことを知っています、
1) sin 2A = 2 sin A cos A
sin 2(30°) = 2 sin 30° cos 30°
sin 60° = 2 × (1/2) × (√3/2) {したがって、sin 30° = 1/2、cos 30° = √3/2、sin 60° = √3/2}
√3/2 = √3/2
L.H.S = R.H.S
2) cos 2A = 2cos2A – 1
cos 2(30°) = 2cos2(30°) – 1
cos 60° = 2(√3/2)2– 1 = 3/2 – 1 {だから、cos 60° = 1/2、cos 30° = √3/2}
1/2 = 1/2
L.H.S = R.H.S
したがって証明されました。
問題 3: Tan x = 3/4 の場合の cos x の値を求めます。
解決:
与えられた場合、tan x = 3/4
私達はことを知っています、
tan x = 反対側/隣接側 = 3/4
斜辺を見つけるには、ピタゴラスの定理を使用します。
斜辺2=反対側2+ 隣接2
H2= 32+42
H2= 9 + 16 = 25
H = √25 = 5
ここで、cos x = 隣接辺/斜辺
cos x = 4/5
したがって、cos x の値は 4/5 になります。
問題 4: ∠B = 45°、BC = 15 インチ、AC = 12 インチの場合、∠C (度単位) と ∠A (度単位) を求めます。

解決:
仮定: ∠B = 45°、BC = a = 15 インチ、AC = b = 12 インチ。
正弦の法則から、次のようになります。
a/sin A = b/sin B = c/sin C
⇒ a/sin A = b/sin B
⇒ 15/sin A = 12/sin 45°
⇒ 15/sin A = 12/(1/√2)
⇒ 15/sin A = 12√2 = 16.97
⇒ A なし = 15/16.97 = 0.8839
⇒ ∠A = 罪-1(0.8839) = 62.11°
三角形の内角の和は180°であることがわかります。
つまり、∠A + ∠B + ∠C = 180°
⇒ 62.11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62.11° + 45°) = 72.89°
したがって、∠A = 62.11°、∠C = 72.89°となります。
問題 5: コサイン関数の半角恒等式を証明してください。
解決:
コサイン関数の半角恒等式は次のとおりです。
cos (θ/2) = ±√[(1 + cos θ)/2]
二重の角度からのアイデンティティから、
cos 2A = 2 cos2A – 1
ここで、A を両側で θ/2 に置き換えます。
⇒ cos 2(θ/2) = 2 cos2(i/2) – 1
⇒ cosθ = 2cos2(i/2) – 1
⇒ 2コス2(θ/2) = cosθ + 1
⇒ コス2(θ/2) = (cosθ + 1)/2
⇒ cos(θ/2) = ±√[(1 + cosθ)/2]
したがって証明されました。
三角法のSin Cos公式に関する練習問題と例
1. sin θ = 3/5 と仮定します。 cosθを求めます。
2. A=45∘ に対する恒等性 sin(2A) = 2 sinA cosA を証明します。
3. cos α = 5/13 の場合。 sin(2a) を求めます。
4. sin θ = cos(90∘−θ) の場合、θ を求めます。
5. Tan β = 2 の場合。ピタゴラス恒等式を使用して sin β と cos β を求めます。
三角法の Sin Cos 公式に関するよくある質問と例
三角法の基本的なサインとコサインの公式は何ですか?
基本的なサインとコサインの公式は、sin θ = 反対側/斜辺、cos θ = 隣接/斜辺です。ここで、θ は直角三角形の角度です。
特殊な角度のサインとコサインはどうやって見つけますか?
0∘、30∘、45∘、60∘、90∘ などの特殊な角度には、三角関数表や単位円の概念を使用して記憶できる特定のサイン値とコサイン値があります。
サイン関数とコサイン関数の間にはどのような関係がありますか?
サイン関数とコサイン関数は恒等式によって関連付けられます。 sinθ = cos(90∘- θ) そしてピタゴラスのアイデンティティ なし 2 θ+cos 2 θ = 1。
サインとコサインの倍角公式はどのように使用しますか?
倍角の公式は次のとおりです。 sin(2θ) = 2sinθcosθ そして cos(2θ)=cos 2 θ – 罪 2 私。 倍角の三角関数を単角で表すために使用されます。
さまざまな象限の角度のサインとコサインの値をどのように見つけますか?
サイン関数とコサイン関数の符号は、角度が存在する象限によって異なります。
- 第 1 象限: sin θ> 0 および cos θ> 0
- 第 2 象限: sin θ> 0 および cos θ <0
- 第 3 象限: sinθ <0 および cosθ < 0
- 第 4 象限: sinθ 0
