放物線の標準形は y = ax です2+ bx + c ここで、a、b、c は実数であり、a はゼロではありません。放物線は、平面内の固定線および固定点から等距離にある平面内のすべての点の集合として定義されます。
この記事では、放物線とは何か、放物線の標準方程式、関連する例などについて詳しく理解します。
目次
パラボラとは何ですか?
放物線は、焦点と呼ばれる点と準線と呼ばれる線から等距離にあるすべての点のセットとして定義される円錐断面です。放物線の標準方程式は、放物線の向き (開く方向) と位置によって異なります。
放物線の方程式
放物線の方程式は標準形式または一般形式で書くことができ、両方を以下に追加します。
放物線の一般方程式
放物線の一般方程式は次のとおりです。
y = 4a(x – h) 2 +k
(または)
x = 4a(y – k) 2 +h
ここで、(h, k) は放物線の頂点です。
放物線の標準方程式
放物線の標準方程式は次のとおりです。
y = 斧 2 + bx + c
(または)
x = です 2 + by + c
ここで、a は決してゼロにはなりません。
放物線の部分
放物線の重要な用語と部分は次のとおりです。
- 集中: 焦点は放物線の不動点です。
- ダイレクトリックス: 放物線の準線は、放物線の軸に垂直な線です。
- フォーカルコード: 放物線の焦点を通過し、放物線を 2 つの異なる点で切断する弦は、焦点弦と呼ばれます。
- 焦点距離: 焦点距離は点 (x) までの距離です。1、 そして1) 焦点からの放物線上。
- 右側: 広角直腸は、放物線の焦点を通過し、放物線の軸に垂直な焦点弦です。直腸広背筋の長さはLL’=4aです。
- 偏心: 点の焦点からの距離と準点からの距離の比は離心率 (e) と呼ばれます。放物線の場合、離心率は 1 に等しい、つまり e = 1 です。
放物線には、放物線の方向とその軸に基づいた 4 つの標準方程式があります。各放物線には、異なる横軸と共役軸があります。
| 放物線の方程式 | 放物線 | 放物線のパラメータの公式 |
|---|---|---|
| そして 2 = 4ax | 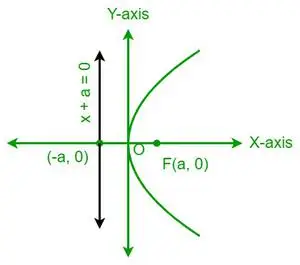 水平放物線 |
|
| そして 2 = -4ax |  水平放物線 |
|
| バツ 2 = 4日 |  垂直放物線 |
|
| バツ 2 = -4ay |  垂直放物線 |
|
以下は、放物線の方程式の標準形式から得られた観察です。
- 放物線は軸に関して対称です。たとえば、y2= 4ax は x 軸に関して対称ですが、x2= 4ay は y 軸に関して対称です。
- 放物線が x 軸に関して対称である場合、放物線は、x 係数が正の場合は右に開き、x 係数が負の場合は左に開きます。
- 放物線が y 軸に関して対称である場合、y 係数が正の場合は放物線は上に開き、y 係数が負の場合は下に開きます。
以下は、対称軸が x 軸または y 軸に平行で、頂点が原点にない場合の放物線の標準方程式です。
| 放物線の方程式 | 放物線 | 放物線のパラメータの公式 |
|---|---|---|
| (そして – k)2= 4a(x – h) |  水平放物線 |
|
| (そして – k)2= -4a(x – h) |  水平放物線 |
|
| (x – h)2= 4a(y – k) |  垂直放物線 |
|
| (x – h)2= -4a(y – k) |  垂直放物線 |
|
放物線の導出方程式
P を放物線上の点とし、その座標は (x, y) です。放物線の定義から、点 P から焦点 (F) までの距離は、同じ点 P から放物線の準線までの距離に等しくなります。ここで、準線上の点 X を考えてみましょう。その座標は (-a, y) です。
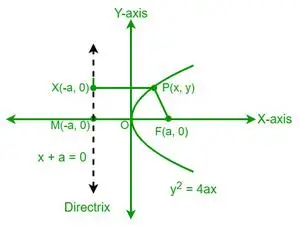
放物線の離心率の定義から、次のようになります。
e = PF/PX = 1
⇒ PF = PX
焦点の座標は (a, 0) です。ここで、座標距離公式を使用して、点 P (x, y) から焦点 F (a, 0) までの距離を求めることができます。
PF = √[(x – a)2+ (および - 0)2]
⇒ PF = √[(x – a)2+と2] ------- (1)
準線の方程式は x + a = 0 です。PX の距離を求めるには、垂直距離の公式を使用します。
PX = (x + a)/√[12+02]
⇒ PX = x +a —————— (2)
PF = PX であることはすでにわかっています。したがって、方程式 (1) と (2) を等しくします。
√[(x – a)2+と2] = (x + a)
両辺を二乗すると、
⇒ [(x – a)2+と2] = (x + a)2
⇒ ×2+a2– 2ax + y2= x2+a2+2ax
⇒そして2– 2ax = 2ax
⇒そして2= 2ax + 2ax ⇒ そして 2 = 4ax
こうして、放物線の方程式が導かれました。同様に、他の 3 つの放物線の標準方程式を導出できます。
- そして2= -4ax
- バツ2= 4日
- バツ2= -4ay
そして 2 = 4ax、および 2 = -4ax、x 2 = 4ay、および x 2 = -4ay は放物線の標準方程式です。
パラボラに関連する記事:
- 円の方程式
- 楕円の方程式
- 双曲線の方程式
- 実生活における放物線の応用
放物線の方程式の例
例 1: 放物線の方程式が y の場合、広背筋直腸、焦点、および頂点の長さを求めます。 2 = 12倍。
解決:
考えると、
放物線の方程式は y です2= 12x
与えられた方程式を標準形式 y と比較することにより、2= 4ax
4a = 12
⇒ a = 12/4 = 3
私達はことを知っています、
放物線の右辺 = 4a = 4 (3) = 12
さて、放物線の焦点 = (a, 0) = (3, 0)
指定された放物線の頂点 = (0, 0)
例 2: X 軸に対して対称で、点 (-4, 5) を通る放物線の方程式を求めます。
解決:
考えると、
放物線は X 軸に関して対称であり、原点に頂点があります。
したがって、方程式は y の形式になります。2= 4ax または y2= -4ax、ここで符号は放物線が左側に開くか右側に開くかによって異なります。
放物線は第 2 象限にある (-4, 5) を通過するため、左に開く必要があります。
したがって、方程式は次のようになります: y2= -4ax
上式に (-4, 5) を代入すると、
⇒ (5)2= -4a(-4)
⇒ 25 = 16a
⇒ a = 25/16
したがって、放物線の方程式は次のようになります。2= -4(25/16)x (または) 4y2= -25x。
例 3: 放物線 x の焦点、軸、準線の方程式、および緯度直腸の座標を求めます。 2 = 16歳。
解決:
考えると、
放物線の方程式は次のとおりです: x2= 16歳
与えられた方程式を標準形式 x と比較することによって2= 4 日、
4a = 16 ⇒ a = 4
y の係数が正であるため、放物線は上に開きます。
また、対称軸は正の Y 軸に沿っています。
したがって、
放物線の焦点は (a, 0) = (4, 0) です。
準線の方程式は y = -a、つまり y = -4 または y + 4 = 0 です。
直腸広背筋の長さ = 4a = 4(4) = 16。
例 4: 放物線の方程式が 2(x-2) の場合、広背筋直腸、焦点、頂点の長さを求めます。 2 + 16 = y。
解決:
考えると、
放物線の方程式は 2(x-2)2+ 16 = および
与えられた方程式を放物線の一般方程式と比較することによって y = a(x – h)2+ k、得られます
a = 2
(h, k) = (2, 16)
私達はことを知っています、
放物線の直腸広腸の長さ = 4a
= 4(2) = 8
ここで、フォーカス = (a, 0) = (2, 0)
さて、頂点 = (2, 16)
例 5: 放物線の方程式は x です 2 – 12x + 4y – 24 = 0 の場合、その頂点、焦点、および準線を見つけます。
解決:
考えると、
放物線の方程式は x です2– 12x + 4y – 24 = 0
⇒ ×2– 12x + 36 – 36 + 4y – 24 = 0
⇒ (x – 6)2+ 4y – 60 = 0
⇒ (x – 6)2= -4(y + 15)
得られた方程式は (x – h) の形式になります。2= -4a(y – k)
-4a = -4 ⇒ a = 1
したがって、頂点 = (h, k) = (6, – 15)
フォーカス = (h, k – a) = (6, -15-1) = (6, -16)
準線の方程式は y = k + a です
⇒ y = -15 + 1 ⇒ y = -14
⇒ y + 14 = 0
放物線の方程式に関する FAQ
放物線の標準方程式はどうやって求めますか?
放物線の標準形は y です2= 4ax または x2= 4日。
放物線の正規方程式とは何ですか?
放物線の法線の方程式 y2= 4ax と傾き m は次のように与えられます。 y = MX – 午前 2 時 – 午前 3
放物線の頂点はどうやって見つけますか?
与えられた放物線の場合: y = ax2+ bx + c その頂点は、式 x = − b/2a を使用して見つけることができます。この x 値を方程式に戻して、対応する y 座標を見つけます。
教師あり機械学習
