トポロジカルソート 有向非巡回グラフ (DAG) すべての有向エッジ u-v に対して、頂点が線形に順序付けされるものです。 で 前に来る で 注文の際に。
注記: グラフが 日 。
例:
推奨される実践方法トポロジーソートを見つけるための DFS ベースのソリューション すでに議論されています。入力: グラフ:
例
モデルの例出力: 5 4 2 3 1 0
説明: トポロジカル ソートの最初の頂点は常に、入次数 0 の頂点 (入力エッジのない頂点) です。次のグラフのトポロジカル ソートは 5 4 2 3 1 0 です。グラフには複数のトポロジカル ソートが存在する場合があります。次のグラフの別のトポロジカル ソートは 4 5 2 3 1 0 です。
トポロジーの順序は一意ではない可能性があります:
トポロジカルソート は、1 つのタスクの完了が、順序が異なる可能性がある他のいくつかのタスクの完了に依存する依存関係の問題です。例を通してこの概念を理解してみましょう。
私たちの仕事は学校に行くことであり、そこに行くためにはまず服を着る必要があるとします。服を着るときの依存関係を以下の依存関係グラフに示します。たとえば、靴下を履く前に靴を履くことはできません。
上の画像から、服を着る方法が複数あることはすでにお気づきかと思いますが、下の画像はそれらの方法の一部を示しています。
挙げていただけますか 考えられるすべてのトポロジカルな順序付け 上記の依存関係グラフのために服を着るのはどうですか?
DFS を使用したトポロジカル ソートのアルゴリズム:
ここでは、深さ優先検索 (DFS) を使用したトポロジカル ソートの段階的なアルゴリズムを示します。
- でグラフを作成します n 頂点と メートル - 方向のエッジ。
- スタックと訪問したサイズの配列を初期化します n 。
- グラフ内の未訪問の頂点ごとに、次の操作を実行します。
- 頂点をパラメータとして DFS 関数を呼び出します。
- DFS 関数では、頂点を訪問済みとしてマークし、頂点のすべての未訪問の近傍に対して DFS 関数を再帰的に呼び出します。
- すべての近傍を訪問したら、頂点をスタックにプッシュします。
- 結局、頂点が訪問されたら、スタックから要素をポップし、スタックが空になるまで出力リストに追加します。
- 結果のリストは、グラフをトポロジー的にソートした順序になります。
トポロジカルソートアルゴリズムの図:
以下の図は、上記のアプローチを示しています。

トポロジカルソートの全体的なワークフロー
ABSCコード
ステップ1:
- 受信ノードがゼロであるため、DFS をノード 0 から開始します。
- ノード 0 をスタックにプッシュし、最小数の隣接ノードを持つ次のノード (ノード 1) に移動します。
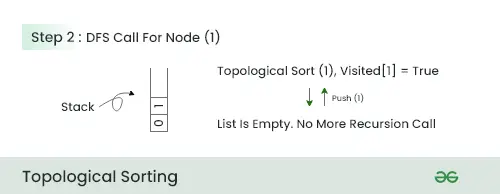
配列リストJavaソートステップ2:
- このステップでは、このノードに隣接するノードがないため、ノード 1 をスタックにプッシュし、次のノードに移動します。
ステップ 3:
- このステップでは、0 と 1 に次いで最小の隣接ノード数を持つノード 2 を選択します。
- ノード 2 の DFS を呼び出し、ノード 2 からのトラバーサルに来るすべてのノードを逆の順序でプッシュします。
- したがって、 3 を押してから 2 を押します。
ステップ 4:
- ここでノード 4 に対して DFS を呼び出します。
- 0 と 1 はすでにスタックに存在するため、ノード 4 をスタックにプッシュして戻るだけです。
ステップ5:
- このステップでは、5 のすべての隣接ノードがすでにスタック内にあるため、ノード 5 をスタックにプッシュして戻ります。
ステップ6: これはトポロジカル ソートの最終ステップで、スタックからすべての要素を取り出し、その順序で出力します。
上記のアプローチの実装を以下に示します。
C++ #include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector>& 形容詞、ベクトル & 訪問済み、スタック & Stack) { // 現在のノードを訪問済みとしてマークする Visited[v] = true; // すべての隣接する頂点に対して繰り返します for (int i : adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, Visited, Stack); } // 現在の頂点を結果を格納するスタックにプッシュします Stack.push(v); } // トポロジカルソートを実行する関数 void topologicalSort(vector>& adj, int V) { スタック スタック; // 結果ベクトルを格納するスタック 訪問済み(V, false); // 再帰的ヘルパー関数を呼び出して、 // すべての頂点から始まるトポロジカル ソートを 1 つずつ格納します。 // for (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout << Stack.top() << ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector> エッジ = { { 0, 1 }、{ 1, 2 }、{ 3, 1 }、{ 3, 2 } }; // 隣接リストベクトルとして表現されるグラフ> adj(V); for (auto i : エッジ) { adj[i[0]].push_back(i[1]); }<< 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }>
ジャワ import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List> adj、boolean[] 訪問、スタック stack) { // 現在のノードを訪問済みとしてマークする Visited[v] = true; // すべての隣接する頂点に対して繰り返します for (int i : adj.get(v)) { if (!visited[i]) topologicalSortUtil(i, adj, Visited, stack); // 結果を格納するスタックに現在の頂点をプッシュします stack.push(v); } // トポロジカルソートを実行する関数 static void topologicalSort(List> adj, int V) { // 結果を保存するスタック スタック スタック = 新しいスタック(); boolean[] 訪問 = new boolean[V]; // 再帰的ヘルパー関数を呼び出して、 // すべての頂点から始まるトポロジカル ソートを 1 つずつ // for (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List> エッジ = 新しい ArrayList(); edges.add(Arrays.asList(0, 1)); edges.add(Arrays.asList(1, 2)); edges.add(Arrays.asList(3, 1)); edges.add(Arrays.asList(3, 2)); // 隣接リストとして表現されるグラフ List> adj = 新しい ArrayList(V); for (int i = 0; i< V; i++) { adj.add(new ArrayList()); } for (List i : エッジ) { adj.get(i.get(0)).add(i.get(1)); トポロジカルソート(adj, V); } }>>
Python3 def topologicalSortUtil(v, adj, visited, stack): # Mark the current node as visited visited[v] = True # Recur for all adjacent vertices for i in adj[v]: if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Push current vertex to stack which stores the result stack.append(v) # Function to perform Topological Sort def topologicalSort(adj, V): # Stack to store the result stack = [] visited = [False] * V # Call the recursive helper function to store # Topological Sort starting from all vertices one by # one for i in range(V): if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Print contents of stack print('Topological sorting of the graph:', end=' ') while stack: print(stack.pop(), end=' ') # Driver code if __name__ == '__main__': # Number of nodes V = 4 # Edges edges = [[0, 1], [1, 2], [3, 1], [3, 2]] # Graph represented as an adjacency list adj = [[] for _ in range(V)] for i in edges: adj[i[0]].append(i[1]) topologicalSort(adj, V)> C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List> adj、bool[] 訪問済み、スタック stack) { // 現在のノードを訪問済みとしてマークする Visited[v] = true; // 隣接するすべての頂点に対して繰り返します foreach(int i in adj[v]) { if (!visited[i]) TopologicalSortUtil(i, adj, Visited, stack); // 現在の頂点をスタックにプッシュし、 // 結果を格納します stack.Push(v); } // トポロジカルソートを実行する関数 static void TopologicalSort(List> adj, int V) { // 結果を保存するスタック スタック スタック = 新しいスタック (); bool[] 訪問 = 新しい bool[V]; // 再帰的ヘルパー関数を呼び出して、 // すべての頂点から始まるトポロジカル ソートを 1 つずつ // for (int i = 0; i< V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Console.Write(stack.Pop() + ' '); } } // ドライバーコード static void Main(string[] args) { // ノード数 int V = 4; // エッジリスト> エッジ = 新しいリスト>{ 新しいリスト { 0, 1 }、新しいリスト { 1, 2 }、新しいリスト { 3, 1 }、新しいリスト { 3, 2 } }; // 隣接リストとして表現されるグラフ List> adj = 新しいリスト>(); for (int i = 0; i< V; i++) { adj.Add(new List ()); foreach(リスト エッジの i) { adj[i[0]].Add(i[1]); TopologicalSort(adj, V); } }>>
JavaScript // Function to perform DFS and topological sorting function topologicalSortUtil(v, adj, visited, stack) { // Mark the current node as visited visited[v] = true; // Recur for all adjacent vertices for (let i of adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Push current vertex to stack which stores the result stack.push(v); } // Function to perform Topological Sort function topologicalSort(adj, V) { // Stack to store the result let stack = []; let visited = new Array(V).fill(false); // Call the recursive helper function to store // Topological Sort starting from all vertices one by // one for (let i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack console.log('Topological sorting of the graph: '); while (stack.length>0) { console.log(stack.pop() + ' '); } } // ドライバー コード (() => { // ノード数 const V = 4; // エッジ constedges = [[0, 1], [1, 2], [3, 1], [3, 2]]; // 隣接リストとして表現されるグラフ const adj = Array.from({ length: V }, () => []) for (let i ofedges) { adj[i[0]].push; (i[1]); } トポロジカルソート(adj, V);>> 出力
Topological sorting of the graph: 3 0 1 2>
時間計算量: O(V+E)。上記のアルゴリズムは、追加のスタックを備えた単純な DFS です。したがって、時間計算量は DFS と同じです
補助スペース: O(V)。スタックには追加のスペースが必要です
BFS を使用したトポロジカル ソート:
C++ #include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * 形容詞; // 隣接リストを含む配列へのポインタ // public: Graph(int V); // コンストラクター void addEdge(int v, int w); // グラフにエッジを追加する関数 void topologicalSort(); // 完全なグラフのトポロジカル ソートを出力します。 }; Graph::Graph(int V) { this->V = V; adj = 新しいリスト [V]; void Graph::addEdge(int v, int w) { adj[v].push_back(w); // w を v のリストに追加します。 } // トポロジカルソートを実行する関数 void Graph::topologicalSort() { // すべての頂点ベクトルの次数を格納するベクトルを作成します in_degree(V, 0); // 隣接リストを走査して、 // 頂点の in_degree を埋めます (int v = 0; v< V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue q; for (int i = 0; i< V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector トップオーダー; // キューから頂点を 1 つずつデキューしてエンキューします // 隣接の次数が 0 になった場合は隣接する頂点 while (!q.empty()) { // キューの前を抽出 (またはデキューを実行) // に追加しますトポロジカル順序 int u = q.front(); q.pop(); トップ_オーダー.プッシュ_バック(u); // デキューされたノード u のすべての隣接ノードを // 反復処理し、 // リストの次数を 1 つ減らします。 ::反復子 itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // in-degree が 0 になった場合、キューに追加 if (--in_degree[*itr ] == 0) q.push(*itr); カウント++; } // サイクルがあったかどうかを確認する if (count != V) { cout<< 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout << i << ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; }> ジャワ import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] 形容詞; // 隣接リスト // グラフの表現 // Constructor Graph(int V) { this.V = V; adj = 新しい ArrayList[V]; for (int i = 0; i< V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = 新しい LinkedList(); for (int i = 0; i< V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList topOrder = 新しい ArrayList(); // キューから頂点を 1 つずつデキューし、 // 隣接する頂点の次数が 0 になった場合、隣接する頂点をキューに入れます。 while (!q.isEmpty()) { // キューの前を抽出して、 // トポロジカルな順序に追加します。 int u = q.poll(); topOrder.add(u); カウント++; // デキューされたノード u のすべての隣接ノードを反復処理し、 // 入次数を 1 ずつ減らします。 // for (int w : adj[u]) { // 入次数が 0 になった場合、 // キューに追加します。 if (--inDegree[w] == 0) q.add(w); } } // サイクルがあったかどうかを確認します if (count != V) { System.out.println('グラフにはサイクルが含まれています'); 戻る; } // (int i : topOrder) のトポロジー順序を出力します。 System.out.print(i + ' '); } } // ドライバー コード public class Main { public static void main(String[] args) { // 上図のグラフを作成します Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println( '次は、指定されたグラフのトポロジカル ソートです'); g.topologicalSort(); } }>> Python3 from collections import defaultdict class Graph: def __init__(self, vertices): # Number of vertices self.V = vertices # Dictionary to store adjacency lists self.adj = defaultdict(list) def addEdge(self, u, v): # Function to add an edge to the graph self.adj[u].append(v) def topologicalSort(self): # Function to perform Topological Sort # Create a list to store in-degree of all vertices in_degree = [0] * self.V # Traverse adjacency lists to fill in_degree of vertices for i in range(self.V): for j in self.adj[i]: in_degree[j] += 1 # Create a queue and enqueue all vertices with in-degree 0 q = [] for i in range(self.V): if in_degree[i] == 0: q.append(i) # Initialize count of visited vertices count = 0 # Create a list to store topological order top_order = [] # One by one dequeue vertices from queue and enqueue # adjacent vertices if in-degree of adjacent becomes 0 while q: # Extract front of queue (or perform dequeue) # and add it to topological order u = q.pop(0) top_order.append(u) # Iterate through all its neighbouring nodes # of dequeued node u and decrease their in-degree # by 1 for node in self.adj[u]: # If in-degree becomes zero, add it to queue in_degree[node] -= 1 if in_degree[node] == 0: q.append(node) count += 1 # Check if there was a cycle if count != self.V: print('Graph contains cycle') return # Print topological order print('Topological Sort:', top_order) # Driver code if __name__ == '__main__': # Create a graph given in the above diagram g = Graph(6) g.addEdge(5, 2) g.addEdge(5, 0) g.addEdge(4, 0) g.addEdge(4, 1) g.addEdge(2, 3) g.addEdge(3, 1) print('Following is a Topological Sort of the given graph') g.topologicalSort()> JavaScript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh> 出力
Following is a Topological Sort of the given graph 4 5 2 0 3 1>
時間計算量:
修復ツール gimp
グラフを構築するための時間計算量は O(V + E) です。ここで、V は頂点の数、E はエッジの数です。
BFS を使用してトポロジカル ソートを実行する場合の時間計算量も O(V + E) です。ここで、V は頂点の数、E はエッジの数です。これは、BFS トラバーサル中に各頂点と各エッジが 1 回訪問されるためです。
空間の複雑さ:
隣接リストを使用してグラフを格納するための空間計算量は O(V + E) です。ここで、V は頂点の数、E はエッジの数です。
追加のスペースは頂点の次数を格納するために使用され、O(V) スペースが必要です。
Javaでのリストの例
キューは BFS トラバーサルに使用され、最大で V 個の頂点を含めることができます。したがって、キューのスペースの複雑さは O(V) です。
全体として、グラフ、次数配列、およびキューのストレージにより、アルゴリズムの空間複雑さは O(V + E) です。
要約すると、提供された実装の時間計算量は O(V + E) であり、空間計算量も O(V + E) です。
注記: ここでは、スタックの代わりに配列を使用することもできます。配列が使用されている場合は、要素を逆の順序で出力して、トポロジカルな並べ替えを取得します。
トポロジカルソートの利点:
- 依存関係に基づいてタスクやイベントをスケジュールするのに役立ちます。
- 有向グラフ内のサイクルを検出します。
- 優先順位制約のある問題を解決するのに効率的です。
トポロジカルソートの欠点:
- 有向非巡回グラフ (DAG) にのみ適用され、巡回グラフには適していません。
- 一意ではない可能性があり、複数の有効なトポロジー順序が存在する可能性があります。
- 多くのノードとエッジを含む大きなグラフの場合は非効率的です。
トポロジカルソートの応用:
- タスクのスケジュール設定とプロジェクト管理。
- パッケージ管理システムにおける依存関係の解決。
- ソフトウェア ビルド システムでのコンパイル順序の決定。
- オペレーティング システムでのデッドロックの検出。
- 大学でのコースのスケジュール設定。
関連記事:
- カーンのトポロジカルソートアルゴリズム
- 有向非巡回グラフのすべての位相的種類