数学ではどこにでも直線の実装があります。これは、幾何学、代数学など、あらゆる分野で実装されています。傾きはラインの方向を定義します。
この記事では、未定義の傾きとゼロの傾きという 2 種類の傾きについて説明します。坂道の種類を理解する前に、まずは坂道について簡単に説明しましょう。
傾斜とは何ですか?
傾きによって定義されるのは、 急峻さ ラインの。 「急峻さ」とは、線の傾きの度合いを指します。つまり、傾きは座標平面上の線の方向を示します。したがって、これは線の勾配としても知られています。スロープ、階段などが実際の坂道の例です。
数学では、傾きは 2 点間の「上昇」と「走行」の比率です。 「ライズ」はラインの垂直方向の変化を意味し、「ラン」はラインの水平方向の変化を意味します。
2 点間の線の傾き (x1、 そして1) と (x2、 そして2) は、点の座標間の差を見つけることによって決定できます。線の傾きは通常、文字「m」で表されます。
m = Δx/Δy = (y2- そして1)/(バツ2- バツ1)または、m = 上昇/走行
未定義の傾き
未定義の傾きは垂直線の傾きです。つまり、線が垂直の場合、傾きは定義されません。未定義の傾きの線は y 軸に平行で、?x の値は 0 です。未定義の傾きの x 座標は、y 座標が何であっても変わりません。未定義の傾きでは、Δy の値はゼロ以外の整数ですが、Δx の値は 0 です。未定義の傾きはゼロの傾きの逆です。立ち上がりとランに関しては、未定義のスロープでの立ち上がりは正または負のいずれかであり、未定義のスロープでのランはゼロです。
m = Δy/Δx = 正または負の Δy/0m の未定義の値は、未定義の傾きと垂直線を表します。
次のグラフでは、未定義の傾きが示されています。以下のグラフの線は、未定義の傾きを示す y 軸に平行です。
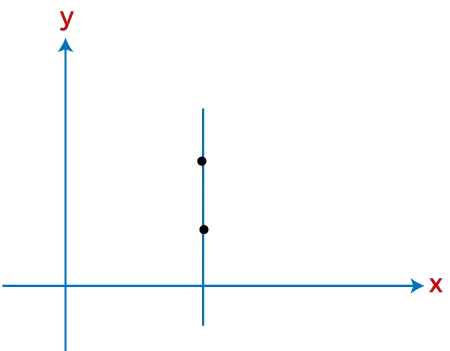
図: 未定義の傾きの表現
上の画像には、未定義の傾きを示す垂直線があります。
ゼロスロープ
傾きがゼロの場合、線は x 軸に平行であり、y 座標は変化しません。水平線の傾きです。立ち上がりと走りに関しては、ゼロスロープでの立ち上がりは 0、ゼロスロープでのランは正になります。
m = Δy/Δx = 0/正のΔxm の値が 0 に等しい場合、線は水平であり、一定の傾きを持ちます。
次のグラフでは、ゼロの傾きが示されています。以下のグラフの線は、ゼロ勾配を示す x 軸に平行であり、ゼロ勾配の y は、x が何であっても同じままです。

図: ゼロスロープの表現
上の画像には、傾きがゼロであることを示す水平線があります。
ここで、未定義の傾きとゼロの傾きの違いを見てみましょう。
ソフトウェアのテストと種類
未定義の傾きとゼロの傾きの違い
未定義の傾きはゼロ傾きの反対です。未定義の傾きとゼロ傾きの差は次のように表にまとめられます。
| はい・いいえ。 | 未定義の傾き | ゼロスロープ |
|---|---|---|
| 1. | それは変数 X によって決まります。 | それは変数 Y によって決定されます。 |
| 2. | 縦線の傾きです。 | 水平線の傾きです。 |
| 3. | 未定義の傾きには具体的な値がないため、存在しない値になります。 | ゼロ傾きは決定された値、つまりゼロです。 |
| 4. | 未定義の傾きの分母はゼロです。 | ゼロ傾きの分子はゼロです。 |
| 5. | 未定義の傾きでは、Y は変化しますが、X は変化しません。 | 未定義の傾きでは、X は変化しますが、Y は変化しません。 |
記事については以上です。私たちは、十分な情報をより簡単な方法で提供するよう努めてきました。未定義の傾き、ゼロの傾き、およびそれらの比較に関する情報を提供することがあなたの役に立つことを願っています。
