球の体積 球体が保持できる液体の量です。球の体積の公式は 4/3πr として与えられます。3。 3 次元空間内で球が占める空間です。単位で測ります3つまり、私3、 cm3、など。球は、幾何学的に丸い形状を持つ 3 次元の固体オブジェクトです。
球の体積は、球の表面が占める空間の合計であり、球の半径の 3 乗に比例します。この記事では、球の体積、球の体積の公式、球の体積の公式の例などについて詳しく学びます。
目次
球の体積とは何ですか?
球の体積は、球の中で占める空間の量です。球は、その表面上のすべての点がその中心から等間隔にある 3 次元の丸い固体形状です。固定距離は球の半径であり、固定点は球の中心です。円を回すと形が変わることに気づきます。円という二次元の物体を回転させると、球という三次元の形状が得られます。
もっと詳しく知る、
- 球
- 球の表面積
球の体積の定義
球の体積は、球の表面によって囲まれた総質量です。球体の内部の 3 次元空間です。それは球の半径によって異なります。以下に追加された画像は、半径 r の球とその体積を示しています。
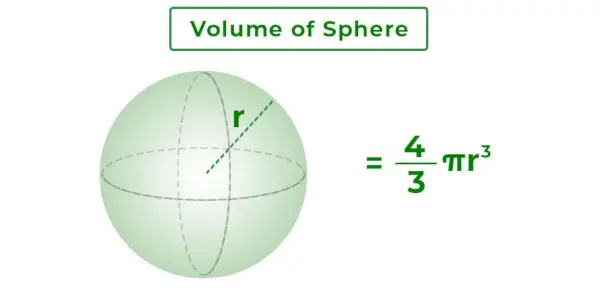
球の体積の計算式
球の体積の公式は、半径が指定された場合に球の体積を求めるために使用される公式です。半径 R の球の球の体積式を以下に追加します。
球の体積公式 = 4/3πr 3
どこ、
- r は球の半径です
- 円周率 は定数であり、その値は 22/7 です
球体は一般に次の 2 つに分類されます。
- 固体球の体積
- 中空球の体積
それらについて詳しく学びましょう。
固体球の体積
中実球とは、内部まで完全に満たされた球のことです。つまり、核まで質量があり、その半径が r のときの体積の公式は次のようになります。
固体球の体積(V) = (4/3)πr 3
中空球の体積
中空球の場合、その内部空間は空であり、その外半径は R そしてその内半径は り、 次に、その体積は次の式を使用して計算されます。
中空球の体積 = (4/3)π(R 3 –r 3 )
球の体積の計算式の導出
球の体積の公式は、次の方法を使用して導き出すことができます。
- 統合の使用
- アルキメデスの使用による円柱、円錐、球の関係
これらの方法について、以下で詳しく説明します。
積分を使用した球の体積
積分アプローチを使用すると、球の体積を簡単に計算できます。
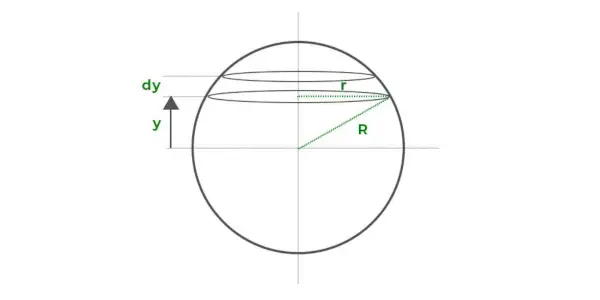
上の図に描かれているように、球の体積が、上下に積み重ねられた一連の薄い円盤で構成されていると仮定します。各薄いディスクの半径は r、厚さは dy (x 軸からの距離 y) です。
ディスクの体積を dV とします。 dV の値は次の式で与えられます。
dV = (πr2) あなた
したがって、dV = π (R2- そして2) あなた
球の総体積は、これらすべての小さな円盤の体積の合計になります。必要な値は、limit -R から R までの式を積分することで得られます。
したがって、球の体積は次のようになります。
V =
⇒ V =
⇒ V =
⇒ V =
⇒ V =
⇒ V =
このようにして、球の体積の公式が導かれます。
アルキメデスの関係を使用した球の体積
アルキメデスがすでに証明したように、円錐、球、円柱が同じ半径 r と同じ高さを持っている場合、それらの体積の比率は 1:2:3 になります。
したがって、次のように言えます。
円柱の体積 = 円錐の体積 + 球の体積
したがって、球の体積 = 円柱の体積 – 円錐の体積
ご存知のとおり、円柱の体積 = πr2h と円錐の体積 = (1/3)πr2h
これらの値を方程式に代入すると、次のようになります。
球の体積 = πr2h – (1/3)πr2h = (2/3)πr2h
円柱の高さは球の直径、つまり 2r に等しいと仮定します。したがって:
球の体積は(2/3)πr 2 h = (2/3)πr 2 (2r) = (4/3)πr 3
また、チェックしてください
- 球状キャップの体積計算式
- 球状扇形の公式
- 球セグメントの計算式
球の体積を計算するにはどうすればよいですか?
球の体積は、球が占める空間です。その体積は次の式を使用して計算できます。 V = 4/3πr 3 。
球の体積を計算するために必要な手順は次のとおりです。
ステップ1: 球の半径の値をマークします。
9月2日: 半径の立方体を求めます。
ステップ 3: 半径の3乗に(4/3)πを掛けます。
ステップ 4: (単位)を追加します3最終的な答えへ。
球の体積を計算する例
例: 半径 7 cm の球の体積を求めます。
与えられた場合、r = 7 cm
V = (4/3)πr3
球の体積、V = ((4/3) × π × 73) cm3
身長 = 1436.8 cm3
したがって、球の体積は 1436.8 cm です。3
続きを読む
- コーンの体積
- 立方体の体積
- シリンダーの体積
球体の体積の例
例 1. 半径 9 cm の球の体積を求めます。
解決:
r = 9 です。
球の体積 = 4/3 πr3
⇒ 球の体積 = (4/3) (3.14) (9) (9) (9)
⇒ 球の体積 = (4) (3.14) (3) (9) (9)
⇒ 球の体積 = 3052 cm3
例 2. 半径 12 cm の球の体積を求めます。
解決:
r = 12 となります。
球の体積 = 4/3 πr3
⇒ 球の体積 = (4/3) (3.14) (12) (12) (12)
⇒ 球の体積 = (4) (3.14) (4) (12) (12)
⇒ 球の体積 = 7234.56 cm3
例 3. 半径 6 cm の球の体積を求めます。
解決:
r = 6 となります。
球の体積 = 4/3 πr3
⇒ 球の体積 = (4/3) (3.14) (6) (6) (6)
⇒ 球の体積 = (4) (3.14) (2) (6) (6)
⇒ 球の体積 = 904.32 cm3
例 4. 半径 4 cm の球の体積を求めます。
解決:
r = 4 となります。
球の体積 = 4/3 πr3
⇒ 球の体積 = (4/3) (3.14) (4) (4) (4)
⇒ 球の体積 = (1.33) (3.14) (4) (4) (4)
⇒ 球の体積 = 267.27 cm3
例 5. 直径 10 cm の球の体積を求めます。
解決:
2r = 10 です
拡張子ファイルjava⇒ r = 5
球の体積 = 4/3 πr3
⇒ 球の体積 = (4/3) (3.14) (5) (5) (5)
⇒ 球の体積 = (1.33) (3.14) (5) (5) (5)
⇒ 球の体積 = 522.025 cm3
例 6. 直径 16 cm の球の体積を求めます。
解決:
あります、2r = 16
⇒ r = 8
球の体積 = 4/3 πr3
⇒ 球の体積 = (4/3) (3.14) (8) (8) (8)
⇒ 球の体積 = (1.33) (3.14) (8) (8) (8)
⇒ 球の体積 = 2138.21 cm3
例 7. 直径 14 cm の球の体積を求めます。
解決:
あります、2r = 14
⇒ r = 7
球の体積 = 4/3 πr3
⇒ 球の体積 = (4/3) (3.14) (7) (7) (7)
⇒ 球の体積 = (1.33) (3.14) (7) (7) (7)
⇒ 球の体積 = 1432.43 cm3
Sphere の練習問題の量
Q1: 直径34cmの球の体積を求めます。
Q2: 内周4cm、外周半径8cmの中空球の体積を求めます。
Q3: 半径14cmの球の体積を求めます。
Q4: 半径が面積144mの正方形の一辺に等しい球の体積はいくらですか2。
Sphere-FAQ の量
球の体積とは何ですか?
球の体積は、球の表面が占める空間です。
球の表面積とは何ですか?
半径 r の球の総表面積は、 面積 = 4πr 2
球の体積を求める公式は何ですか?
半径 r の球の体積は、 体積 = 4/3πr 3
半球の体積はどのようにして求められるのでしょうか?
半径 r の半球の体積は、 体積 = 2/3πr 3
球と半球の体積の比率は何ですか?
球と半球の半径が同じ場合、それらの体積の比率は次のようになります。
で 1 : で 2 = (4/3πr 3 ) : (2/3πr 3 ) = 2 : 1
球の体積の単位は何ですか?
球の体積はm単位で測定されます3、 cm3、リットルなど。 メートル 3 標準の測定単位です。
球の半径が半分になったときの球の体積はいくらですか?
球の体積 = (4/3)πr3= (4/3)π(r/2)3= (4/3)π(r3/8) = 体積/8。したがって、球の体積は 8 分の 1 になります。
