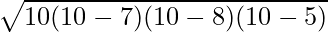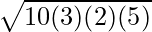鋭角三角形とは、三角形の角がすべて鋭角である三角形のことです。三角形の角度の合計特性により、三角形は直角または鈍角のいずれかの角度を 1 つだけ持つことができます。したがって、3 つの角すべてが鋭角、つまり 90 度未満の値を持つ三角形は、鋭角三角形と呼ばれます。

三角形は、その内角の種類により、鋭角三角形、鈍角三角形、直角三角形の3つに分類されます。この記事では、鋭角三角形、その種類、特性などについて詳しく学びましょう。

鋭角三角形とは何ですか?

アン 鋭角な三角形 は、3 つの内角がすべて鋭角である三角形として定義されます。つまり、その値は 0° から 90° の間です。三角形の種類に応じて、鋭角三角形の辺の長さは等しい場合もあれば、等しくない場合もあります。鋭角の三角形も、三角形の角度の合計プロパティに従います。

以下の図は、内角が 45°、35°、80° である鋭角三角形です。 3 つの内角が 90° 未満であるため、指定された三角形は鋭角の三角形です。

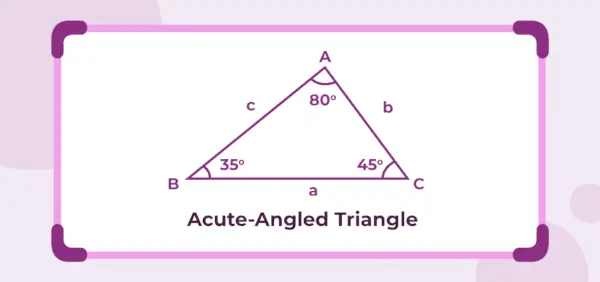
鋭角三角形の定義

鋭角三角形は、名前が示すように、三角形の 3 つの角がすべて鋭角である三角形として定義されます。鋭角三角形の辺は等しい場合もあれば等しくない場合もあり、それに基づいて、さらに 3 つの部分に分割されます。これについては、以下の記事で説明します。

鋭角三角形の種類

鋭角三角形は、三角形の辺の長さによって3種類に分類されます。

• 正三角形の鋭角
• 鋭二等辺三角形
• 不等辺鋭角三角形

それでは、それらについて詳しく見ていきましょう。

正三角形の鋭角

正三角形とも呼ばれる正三角形は、すべての角が鋭角であり、すべての角が等しく、正三角形の辺も等しい三角形です。正三角形の各角度は常に 60° になります。

鋭二等辺三角形

鋭角二等辺三角形とは、すべての角が鋭角であり、三角形の任意の２つの角とこれらの角に対応する辺が等しい三角形である。つまり、鋭角二等辺三角形では 2 つの辺があり、それらの対応する角度が等しいということです。

不等辺鋭角三角形

不等辺鋭角三角形とは、すべての角が鋭角であり、等しい 2 つの角や 2 つの辺がない三角形です。つまり、不等辺鋭角三角形には等しい辺も角度もありません。

鋭角三角形の性質

以下に、鋭角三角形の重要な特性をいくつか示します。

• 鋭角三角形の内角は鋭角です。つまり、角度は 0°より大きく 90°より小さいです。
• 鋭角三角形の内角は、角度の合計のプロパティに従います。つまり、鋭角三角形の角度の合計は 180°です。
• 正三角形の各内角は 60°であるため、正三角形は常に鋭角の三角形です。
• 三角形は、同時に直角三角形と鋭角三角形になることはできません。
• 三角形は、同時に鋭角三角形と鈍角三角形になることはできません。
• 鋭角三角形では、最小角の反対側が最小となり、その逆も成り立ちます。
• 同様に、最大角度の反対側が最大となり、その逆も同様です。

鋭角三角形の公式

面積と周長は、以下で説明する鋭角三角形の 2 つの基本公式です。

鋭角三角形の周囲長

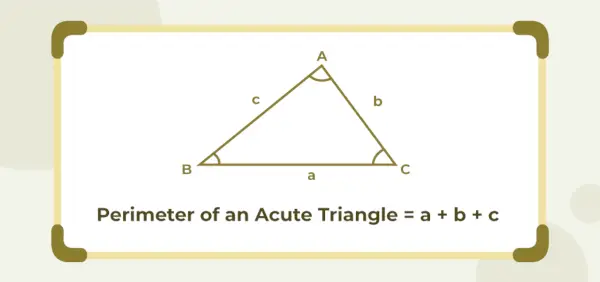
鋭角な三角形の周囲の長さは、その 3 つの辺の長さの合計に等しくなります。 a、b、c が鋭角三角形の辺の長さである場合、その周囲長は (a + b + c) 単位で与えられます。

鋭角三角形の周囲長 = (a + b + c) 単位

どこ ある 、 b 、 そして c は三角形の辺の長さです。

続きを読む、 三角形の周囲長

鋭角三角形の面積

三角形の面積は、2 次元平面内の三角形の 3 つの辺で囲まれた空間の合計として定義されます。

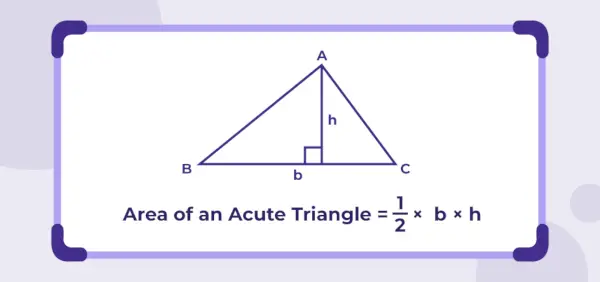
鋭角三角形の面積 = 1/2 × b × h

どこ、

b は底辺の長さ、h は三角形の高さです。

続きを読む、 三角形の面積

ヘロンの公式による鋭角三角形領域

鋭角三角形の 3 つの辺の長さが指定されている場合、その面積はヘロンの公式を使用して計算できます。

鋭角三角形の面積 =

どこ、

s は半周長であり、 s = (a + b + c)/2 、 あなた 、 b 、 そして c は三角形の辺の長さです。

続きを読む、 ヘロンの公式

C++は文字列に変換します

三角形の重要な用語

鋭角三角形に関連するさまざまな用語は次のとおりです。

中心付近

三角形の3つの頂点を通る円の中心を三角形の外心といいます。垂直二等分線の交点を取ることによって計算されます。鋭角の三角形の場合、外心は常に三角形の内側にあります。

中心

三角形の３辺に接する円の中心を三角形の内心といいます。これは、角の二等分線の交点を取ることによって計算されます。鋭角の三角形の場合、内心は常に三角形の内側にあります。

重心

三角形の中線の交点は三角形の重心と呼ばれます。鋭角の三角形の場合、三角形の重心は常に三角形の内側にあります。

直交中心

三角形の高度の交点は、三角形の垂心と呼ばれます。鋭角の三角形の場合、三角形の垂心は常に三角形の内側にあります。

鋭角三角形の解決例

例 1: 次の角度のうち、鋭角三角形を形成できるのはどれですか?

a) 65°、75°、50° b) 95°、40°、45° c) 70°、40°、70° d) 90°、45°、45°

解決：

鋭角三角形のすべての角度は、その尺度が 90 度未満である鋭角であることがわかります。

また、それらは三角形の角度の合計のプロパティに従います。つまり、すべての角度の合計は 180 度になります。

a) 65°、75°、50°

ここでは、すべての角度が鋭角ですが、角度の合計のプロパティに従っていないため、三角形は作成できません。

65°+75°+50°=190°（三角形は不可）

b) 95°、40°、45°

ここでは、三角形の角度和の性質に従うため、三角形が可能です。

95°+40°+45°=180

しかし、三角形の角度を観察していると、鈍角 95° であることがわかりました。したがって、この三角形は鋭角三角形ではありません。

c) 70°、40°、70°

ここでは、三角形の角度の和の性質に従うため、三角形が可能です。

70°+40°+70°=180

そして、三角形の角度を観察すると、すべての角度が鋭角であることがわかりました。したがって、三角形は鋭角三角形です。

d) 90°、45°、45°

ここでは、三角形の角度和の性質に従うため、三角形が可能です。

90°+45°+45°=180

しかし、三角形の角度を観察していると、直角90°であることがわかりました。したがって、この三角形は鋭角三角形ではありません。

例 2: 辺が XY = 8 単位、YZ = 5 単位、XZ = 9 単位である鋭角三角形 XYZ の周囲長を求めます。

解決：

考えると、

鋭角三角形の辺、

• XY(x) = 8 単位
• YZ(y) = 5 単位
• XZ(z) = 9 単位

私達はことを知っています、

鋭角三角形の周囲長 (P) = x + y + z

⇒ P = (8 + 5 + 9) 単位

⇒ P = 22 単位

したがって、鋭角三角形の周囲長は 22 単位になります。

例 3: 高さが 12 単位、底辺が 15 単位の鋭角三角形の面積を求めます。

解決：

考えると、

• 三角形の高さ (h) = 12 単位
• 三角形の底辺の長さ (b) = 15 単位

私達はことを知っています、

三角形の面積 (A) = 1/2 × b × h

⇒ A = 1/2 × 12 × 15

⇒ A = 1/2 × 180

⇒ A = 90 平方ユニット。

したがって、指定された鋭角三角形の面積は 90 平方単位です。

例 4: 辺が AB = 5 cm、BC = 7 cm、AC = 8 cm である鋭角三角形の面積を求めます。

解決：

ビンからBCDへ

考えると、

鋭角三角形の辺、

• AB = c = 5 単位
• BC = a = 7 単位
• AC = b = 8 ユニット

私達はことを知っています、

三角形の面積 =

⇒ あ=

⇒ あ=

⇒ A = √(300) 平方センチメートル

⇒ A = 10√3 平方センチメートル

したがって、与えられた鋭角三角形の面積は 10√3 平方センチメートルです。

鋭角三角形に関するよくある質問

Q1: 鋭角とは何ですか?

答え：

0°から90°までの角度を鋭角と呼びます。つまり、鋭角の最小値は 0°より大きく、鋭角の最大値は 90°より大きくなります。

Q2: 鋭角三角形とは何ですか?

答え：

鋭角三角形は、3 つの内角がすべて鋭角である三角形です。つまり、角度の値が 0° から 90° の間にあります。

Q3: 正三角形は常に鋭角三角形ですか?

答え：

はい、正三角形は常に鋭角な三角形です。鋭角三角形とは、すべての角が鋭角である角度のことで、正三角形ではすべての角が60°、つまり鋭角になります。したがって、正三角形は常に鋭角な三角形です。

Q4: 鋭角三角形にはどのような種類がありますか?

答え：

鋭角三角形は次の 3 つのタイプに分類されます。

• 不等辺鋭角三角形
• 鋭二等辺三角形
• 正三角形の鋭角

Q5: 三角形が鋭角三角形かどうかを確認するにはどうすればよいですか?

答え：

内角が 90° 未満、つまりすべての内角が鋭角である三角形は、鋭角三角形と呼ばれます。三角形の角度を観察するだけで、その三角形が鋭角三角形であるかどうかを確認できます。