理解する前に B木 そして B+ ツリー 違いがあるため、B ツリーと B+ ツリーを別々に理解する必要があります。
Bツリーとは何ですか?
B木 は自己平衡ツリーであり、m がツリーの順序を定義する m-way ツリーです。 Bツリー の一般化です 二分探索ツリー この場合、ノードは、 の値に応じて複数のキーと 2 つ以上の子を持つことができます。 メートル 。 B ツリーでは、データは、左側のサブツリーに低い値、右側のサブツリーに高い値を持つソートされた順序で指定されます。
mysql ubuntuを再起動します
B ツリーのプロパティ
B ツリーのプロパティは次のとおりです。
- B ツリーでは、すべてのリーフ ノードが同じレベルにある必要がありますが、バイナリ ツリーの場合、リーフ ノードは異なるレベルにあってもかまいません。
例を通してこの特性を理解しましょう。
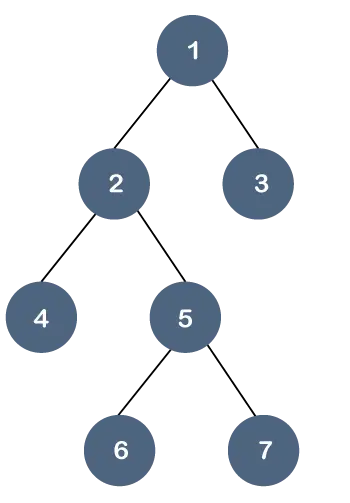
上記のツリーでは、すべてのリーフ ノードが同じレベルにありませんが、最大で 2 つの子を持ちます。したがって、上記の木は 二分木 しかしBツリーではありません。
- Btree の次数が m の場合、各ノードは最大で次数を持つことができます。 メートル 最小の子の場合、リーフ ノードには子が 0 つあり、ルート ノードには 2 つの子があり、内部ノードの上限は m/2 です。
- 各ノードは最大 (m-1) 個のキーを持つことができます。たとえば、m の値が 5 の場合、キーの最大値は 4 です。
- ルート ノードには最小 1 つのキーがあり、ルート ノードを除く他のすべてのノードには (m/2 マイナス - 1 の天井) 最小キーがあります。
- B ツリーに挿入を実行すると、ノードは常にリーフ ノードに挿入されます。
1 から 10 までの値を挿入して次数 3 の B ツリーを作成するとします。
ステップ1: まず、以下に示すように 1 つの値を持つノードを作成します。

ステップ2: 次の要素は 2 で、以下に示すように 1 の後に来ます。

ステップ 3: 次の要素は 3 で、以下に示すように 2 の後に挿入されます。

各ノードは最大 2 つのキーを持つことができることがわかっているため、このノードを中央の要素で分割します。中央の要素は 2 なので、その親に移動します。ノード 2 には親がないため、以下に示すようにルート ノードになります。

ステップ 4: 次の要素は 4 です。4 は 2 および 3 より大きいため、以下に示すように 3 の後に追加されます。

ステップ5: 次の要素は 5 です。5 は 2、3、4 より大きいため、以下に示すように 4 の後に追加されます。

各ノードは最大 2 つのキーを持つことができることがわかっているため、このノードを中央の要素で分割します。中央の要素は 4 なので、その親に移動します。親はノード 2 です。したがって、以下に示すように、2 の後に 4 が追加されます。

ステップ6: 次の要素は 6 です。6 は 2、4、5 より大きいため、以下に示すように 6 は 5 の後に来ます。

ステップ 7: 次の要素は 7 です。7 は 2、4、5、6 より大きいため、以下に示すように 7 は 6 の後に来ます。

各ノードは最大 2 つのキーを持つことができることがわかっているため、このノードを中央の要素で分割します。中央の要素は 6 なので、次のように親に移動します。

ただし、ノードには最大 2 つのキーを含めることができるため、4 の後に 6 を追加することはできません。そのため、このノードを中央の要素で分割します。中央の要素は 4 なので、その親に移動します。ノード 4 には親がないため、以下に示すように、ノード 4 がルート ノードになります。

B+ ツリーとは何ですか?
の B+ ツリー ツリーの根元から葉までのすべてのパスが同じ長さであるため、高度な自己バランス型ツリーとしても知られています。ここで、同じ長さは、すべてのリーフ ノードが同じレベルに存在することを意味します。リーフ ノードの一部が第 3 レベルで発生し、一部が第 2 レベルで発生するということは起こりません。
B+ ツリー インデックスはマルチレベル インデックスとみなされますが、B+ ツリー構造はマルチレベル インデックス シーケンシャル ファイルとは異なります。
なぜ B+ ツリーが使用されるのですか?
B+ ツリーは、B+ ツリーのインデックス付き構造を使用してインデックス付きの方法でレコードを格納することにより、レコードを非常に効率的に格納するために使用されます。マルチレベルのインデックス作成により、データへのアクセスがより高速かつ簡単になります。
B+ ツリーのノード構造
B+ ツリーのノード構造には、次の図に示すポインターとキー値が含まれています。

上記の B+ ツリー ノード構造でわかるように、n-1 個のキー値 (k1kへn-1) および n ポインター (p1上n)。
ノードに配置された検索キーの値はソートされた順序で保持されます。したがって、私が
Pythonは数値です
さまざまなタイプのノードに対する制約
「b」を B+ ツリーの次数とします。
非リーフノード
「m」がノードの子の数を表すとすると、ツリーの順序と子の数の関係は次のように表すことができます。

k が検索キーの値を表すものとします。ツリーの順序と検索キーの関係は次のように表すことができます。
ポインターの数は検索キーの値に 1 を加えたものに等しいことがわかっているため、数学的には次のように書くことができます。
ポインター (または子) の数 = 検索キーの数 + 1
したがって、ポインターの最大数は「b」となり、ポインターの最小数は b/2 の上限関数になります。
リーフノード
リーフ ノードは、B+ ツリーの最後のレベルにあるノードであり、各リーフ ノードは 1 つのポインタのみを使用して相互に接続し、リーフ レベルでの順次アクセスを提供します。
リーフ ノードの子の最大数は次のとおりです。

検索キーの最大数は次のとおりです。

ルートノード
ルート ノードの場合の子の最大数は次のとおりです。 b
子供の最小数は次のとおりです: 2
B+ ツリーの特殊なケース
ケース 1: ルート ノードがツリー内の唯一のノードである場合。この場合、ルートノードがリーフノードになります。
この場合、子の最大数は 1、つまりルート ノード自体ですが、子の最小数は b-1 で、これはリーフ ノードの数と同じです。
B+ ツリーのリーフ ノードの表現

上図では「。」はポインタを表し、10、20、および 30 はキー値です。上の図に示すように、ポインタにはキー値が格納されるアドレスが含まれています。
B+ツリーの例

上の図では、ノードには 3 つのキー値 (9、16、25) が含まれています。9 の前に表示されるポインタには、k で表される 9 未満のキー値が含まれています。私。 16 より前に表示されるポインターには、kj で表される 9 以上 16 未満のキー値が含まれます。 25 より前に表示されるポインタには、k で表される 16 以上 25 未満のキー値が含まれます。n。
B ツリーと B+ ツリーの違い

B ツリーと B+ ツリーの違いは次のとおりです。
| B木 | B+ ツリー |
|---|---|
| B ツリーでは、すべてのキーとレコードが内部ノードとリーフ ノードの両方に保存されます。 | B+ ツリーでは、キーは内部ノードに格納されるインデックスであり、レコードはリーフ ノードに格納されます。 |
| B ツリーではキーを繰り返し格納することができないため、キーやレコードの重複がありません。 | B+ ツリーでは、キーの出現に冗長性が存在する可能性があります。この場合、レコードはリーフ ノードに格納され、キーは内部ノードに格納されるため、内部ノードに冗長キーが存在する可能性があります。 |
| Btreeではリーフノード同士はリンクされていません。 | B+ ツリーでは、リーフ ノードが相互にリンクされてシーケンシャル アクセスが提供されます。 |
| Btree では、レコードがリーフ ノードまたは内部ノードに格納されるため、検索はあまり効率的ではありません。 | B+ ツリーでは、すべてのレコードがリーフ ノードに格納されるため、検索が非常に効率的または高速になります。 |
| 内部ノードの削除は、削除されたキーの子も考慮する必要があるため、非常に遅く、時間のかかるプロセスです。 | B+ ツリーでの削除は、すべてのレコードがリーフ ノードに格納されているため、ノードの子を考慮する必要がなく、非常に高速です。 |
| Btreeではシーケンシャルアクセスはできません。 | B+ ツリーでは、すべてのリーフ ノードがポインタを介して接続されているため、シーケンシャル アクセスが可能です。 |
| Btreeでは、幅に比べて高さが増加するため、より多くの分割操作が実行されます。 | B+ ツリーは高さに比べて幅が大きくなります。 |
| Btree では、各ノードに少なくとも 2 つのブランチがあり、各ノードにいくつかのレコードが含まれるため、データを取得するためにリーフ ノードまでトラバースする必要はありません。 | B+ ツリーでは、内部ノードにはポインターのみが含まれ、リーフ ノードにはレコードが含まれます。すべてのリーフ ノードは同じレベルにあるため、データを取得するにはリーフ ノードまでトラバースする必要があります。 |
| ルート ノードには少なくとも 2 ~ m 個の子が含まれます。m はツリーの順序です。 | ルート ノードには少なくとも 2 ~ m 個の子が含まれます。m はツリーの順序です。 |
