カードの確率は、トランプのデッキに関係するイベントの確率です。ご存知のとおり、確率はあらゆる事象の可能性の計算を扱う数学の重要なトピックの 1 つです。簡単に言うと、カードの確率は、カードの山からカードを引く確率を求める確率の一部です。この記事では、カードの確率表、トランプの確率、カードの確率の求め方、カードの確率の解決例について詳しく説明し、カードの確率について学びます。カードの確率のトピックから学習を始めましょう。
確率とは何ですか?
確率は、あらゆる出来事が起こるか起こらないかの可能性を研究する数学の分野です。数学的には、イベントの結果の総数 (サンプル空間) に対する好ましい結果の数の比率に他なりません。
確率の実例としては、次のようなものがあります。
- カードゲームをプレイして、ゲームの勝敗の確率を調べます。
- 雨を予測する天気予報。
- 候補者が勝つか負けるかを決定する選挙結果。
- 受験者が合格するか不合格になるかを識別するための試験結果。
確率の公式
E がサンプル空間 S のイベントで、好ましい結果の数が n(E) の場合、イベント E の確率、つまり P(E) は次の式で与えられます。
P(E) = n(E) / n(S)
カードの確率とは何ですか?
カードを引く確率、またはデッキからカードのコレクションを引く確率は、カード確率と呼ばれます。簡単に言えば、トランプに関係する確率をカード確率といいます。これは確率の一種であるため、常に 0 と 1 の間にあります。たとえば、トランプのデッキからエースを引く確率を求めなければならない場合、つまり 4/52 = 1/13 [エースが 4 枚あるため、 52 枚のカードのデッキで]。
確率におけるトランプのデッキ
Deck of Cards は、何千年も前から存在していると思われる 52 枚のカードのコレクションです。トランプまたはトランプの起源はインドまたは中国のいずれかであると考えられており、これらのカードの最初の文書化された証拠は 9 に見つかります。番目-世紀の中国、唐の時代。これらのカードは現代のカードに似ており、4 つのスートに分かれていますが、それらのスートの名前とシンボルは異なります。つまり、コイン、コインの連なり、無数、無数のカードです。
現代では、これらのカードにはさまざまなデザインがあり、スペード (♠)、クラブ (♣)、ハート (❤)、ダイヤモンド (◆) の 4 つのスートに分けられます。選択された 1 枚のカードの場合、サンプル空間は 52 です。つまり、デッキから選択された 1 枚のカードの結果の総数は 52 です。
トランプの n(S) = 52
デッキ内のカードの種類
どのデッキのカードもさまざまな方法で分類できます。カードを分類できるパラメータには次のようなものがあります。
- 色に基づいて
- スーツをベースに
この分類を次のように詳しく理解しましょう。
色に基づいて
色に基づいて、トランプのデッキは 2 つのカテゴリに分類できます。
- レッドカード
- ブラックカード
合計 52 枚のカードが赤と黒のカードに均等に分割されます。つまり、デッキには赤のカードが 26 枚、黒のカードが 26 枚あります。
スーツをベースに
カードデッキには次の 4 つのスートがあります。
- ハート(❤)
- ダイヤモンド(◆)
- クラブ (♣)
- スペード (♠)
これらの他に、カードのランクに基づいたカードの分類がもう 1 つあります。
- エース
- ナンバーカード
- フェイスカード
エース
エースは、ゲームに基づいて最も重要または最も重要でないカードの 1 つです。このカードには A と書かれており、各スートにはそのようなカードが 1 枚、つまりエース カードが 4 枚あります。
ナンバーカード
2 から 10 まで、スートごとに 9 枚のカードがあり、合計 36 枚のカードがあります。
Javaスタック
フェイスカード
名前が示すように、絵カードには、カード上の人物または人物の顔が含まれています。各スートには 3 枚のカード (ジャック、クイーン、キング) があります。したがって、合計 12 枚の絵札があります。
これらすべての分類を次の表に示します。
| トランプ (52 枚) | ||||
|---|---|---|---|---|
| カラーカード | ブラックカード (26枚) | レッドカード (26枚) | ||
| スーツ | スペード(13枚) | クラブ(13枚) | ハート(13枚) | ダイヤモンド(13枚) |
| フェイスカード (デッキに 12 枚のカードと各スートに 3 枚のカード) | K(キング) | K(キング) | K(キング) | K(キング) |
| Q(クイーン) | Q(クイーン) | Q(クイーン) | Q(クイーン) | |
| J(ジャック) | J(ジャック) | J(ジャック) | J(ジャック) | |
| ナンバーカード (デッキに 36 枚のカードとスーツに 9 枚のカード) | 10 | 10 | 10 | 10 |
| 9 | 9 | 9 | 9 | |
| 8 | 8 | 8 | 8 | |
| 7 | 7 | 7 | 7 | |
| 6 | 6 | 6 | 6 | |
| 5 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | |
| 3 | 3 | 3 | 3 | |
| 2 | 2 | 2 | 2 | |
| エースカード (デッキに 4 枚のカードとスーツに 1 枚のカード) | A(エース) | A(エース) | A(エース) | A(エース) |
トランプのデッキ表
次の表は、トランプのデッキの分類を表しています。
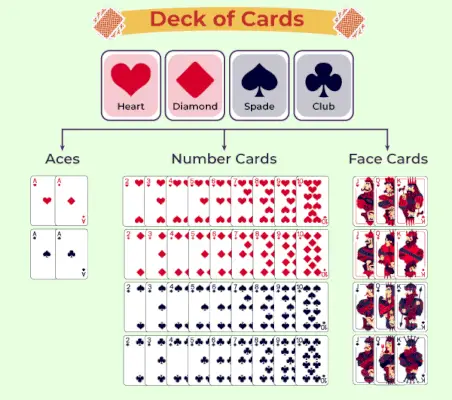
トランプのカードの確率
カードの確率における一般的なイベントのいくつかを次の表で説明します。
| カードを引くイベントE | 確率P(E) |
|---|---|
| エース | P(E) = 4 / 52 = 1 / 13 |
| 王様 | P(E) = 4 / 52 = 1 / 13 |
| ナンバーカード | P(E) = 36 / 52 = 9 / 13 |
| フェイスカード | P(E) = 12 / 52 = 3 / 13 |
| スペードカード | P(E) = 13 / 52 = 1 / 4 |
| レッドカード | P(E) = 26 / 52 = 1 / 2 |
カードの確率を調べるには?
カードに関係するイベントの確率を見つける手順は、他のすべての確率と同じであり、次のように与えられます。
ステップ1: まず、与えられた質問から好ましい結果の数を見つけます。
ステップ2: 次に、結果の合計数を求めます。
ステップ 3: 確率の公式を適用してカードの確率を求めます。
例: トランプのデッキからエースを引く確率はどれくらいですか?
答え:
ここで、Eはエースカードを引くイベントです
デッキ内の結果の総数 n(S) = 52
有利な結果の数 = n(E) = デッキからエース カードを引く = 4 (1 つのデッキにはエース カードが 4 枚あります)
P(E) = n(E) / n(S) = 4 / 52
P(E) = 1 / 13
エースカードを引く確率 = 1 / 13
カードの確率に関するサンプル質問
問題 1: トランプのデッキから次のカードを引く確率はいくらですか?
(i) スペード
(ii) ブラックカード
(iii) ナンバーカード
解決:
(i) ここで、E はスペードカードを引くイベントです
デッキ内の結果の総数 n(S) = 52
有利な結果の数 = n(E) = デッキからスペード カードを引く = 13 (1 つのデッキには各スートのカードが 13 枚あります)
P(E) = n(E) / n(S) = 13 / 52
P(E) = 1 / 4
スペードを引く確率 = 1 / 4
(ii) ここで、E はブラックカードを引くイベントです
デッキ内の結果の総数 n(S) = 52
有利な結果の数 = n(E) = デッキから黒のカードを引く = 26 (1 つのデッキには 26 枚の黒のカードがあります)
Javaの単純な日付フォーマッタP(E) = n(E) / n(S) = 26 / 52
P(E) = 1 / 2
ブラックカードを引く確率 = 1 / 2
(iii) ここで、E はナンバーカードを引くイベントです。
デッキ内の結果の総数 n(S) = 52
有利な結果の数 = n(E) = デッキから数字カードを引く = 36 (1 つのデッキには 36 枚の数字カードがあります)
P(E) = n(E) / n(S) = 36 / 52
P(E) = 9 / 13
数字カードを引く確率 = 9 / 13
問題 2: トランプのデッキから次のカードを引く確率はいくらですか?
(i) キングカードまたはブラックカード
(ii) 赤とエースのカード
解決:
(i) ここで、E はキングまたはブラックカードを引くイベントです。
デッキ内の結果の総数 n(S) = 52
有利な結果の数 = n(E) = デッキからキングまたはブラック カードを 1 枚引く = 26 + 2 = 28 (1 つのデッキには 26 枚のブラック カードがあり、そのうち 2 枚がキングで残り 2 枚が黒のキングになります)
P(E) = n(E) / n(S) = 28 / 52
P(E) = 7 / 13
キングまたはブラック カードを引く確率 = 7 / 13
(ii) ここで、Eはレッドとエースのカードを引くイベントです
デッキ内の結果の総数 n(S) = 52
有利な結果の数 = n(E) = デッキから赤とエースのカードを引く = 2 (赤のカードは 26 枚あり、そのうち 2 枚はエース カードです)
質問によると、引いたカードは赤とエースの両方でなければなりません。したがって、n(E) = 2
P(E) = n(E) / n(S) = 2 / 52
P(E) = 1 / 26
赤とエースのカードを引く確率 = 1 / 26
問題 3: トランプのデッキから次のカードを引く確率はいくらですか?
(i) クラブカード以外のカード
(ii) フェイスカード以外のカード
解決:
(i) ここで、E は非クラブカードを引くイベントです。
デッキ内の結果の総数 n(S) = 52
有利な結果の数 = n(E) = デッキから非クラブ カードを引く = 39 (1 つのデッキには 13 のクラブがあり、非デッキ = 52 – 13 = 39)
P(E) = n(E) / n(S) = 39 / 52
P(E) = 3 / 4
char から int Java へクラブ以外のカードを引く確率 = 3 / 4
(ii) ここで、E は非フェイスカードを引くイベントです。
デッキ内の結果の総数 n(S) = 52
有利な結果の数 = n(E) = デッキから非フェイス カードを引く = 40 (1 つのデッキには 12 枚のフェイス カードがあり、非デッキ = 52 – 12 = 40)
P(E) = n(E) / n(S) = 40 / 52
P(E) = 10 / 13
クラブ以外のカードを引く確率 = 10 / 13
問題 4: 赤でも絵札でもないカードを引く確率はいくらですか?
解決:
ここで、Eは赤でも絵札でもないカードを引くイベントです
デッキ内の結果の総数 n(S) = 52
有利な結果の数 = n(E) = 山札から赤も絵札も引きません。
レッドカードの合計 = 26
デッキには合計 12 枚の絵札がありますが、6 枚の赤い絵札がすでに取り除かれています。したがって、残りの絵札 = 12 – 6 = 6
n(E) = 26 + 6 = 32
P(E) = n(E) / n(S) = 32/52
P(E) = 8 / 13
赤でも絵札でもないカードを引く確率 = 8 / 13
問題 5: 1 枚目のカードがハートで 2 枚目のカードがダイヤモンドの場合、置換付きのカード 1 組から 2 枚のカードを引く確率はいくらですか?
解決:
最初のカードをハートとして引く確率 = 13 / 52
最初のカードを引いた後、そのカードは取り除かれます。
2 枚目のカードをダイヤモンドとして引く確率 = 13 / 51
1 枚目のカードがハートで 2 枚目がダイヤになる確率 = (13 / 52) × (13 / 51)
最初のカードがハートとして描かれ、2 番目のカードがダイヤモンドとして描かれる確率 = 13 / 204
カードの確率に関するよくある質問
1. カードの確率とは何ですか?
トランプからカードを引く確率をカード確率といいます。
2. トランプのカードの種類をリストします。
トランプには 4 種類のスートがあります。彼らです:
- ハート
- ダイヤモンド
- スペード
- クラブ
3. 山札からカードを 1 枚引いた場合、山札のサンプルスペースはどれくらいですか?
1 枚のカードが引かれたときのカード デッキのサンプル スペースには、52 の結果が含まれます。
4. 確率を求める式を書きます。
確率を求める公式は次のようになります。
イベントの確率 = 有利なイベントの数 / 結果の総数
または
P(E) = n(E) / n(S)
5. トランプのカードには何枚の絵札が入っていますか?
トランプには 12 枚の絵札があります。
