複素数は実数の自然な連続です。現代では、複素数はデジタル信号処理、暗号化、および多くのコンピューター関連分野などの多くの分野で使用されています。

この記事では、虚数、複素数とその種類、複素数に対するさまざまな演算、複素数の性質、複素数の応用などについて学びます。

複素数の定義

複素数 は 数字 形の (a + i b) どこ ある & b は実数であり、 私 は√-1を表すiotaと呼ばれる虚数単位です。たとえば、2 + 3i は、2 が実数、3i が虚数である複素数です。複素数は、a + ib として書くことができます。ここで、a と b は、次の数直線上で表すことができる有理数です。 無限大 。

PowerShell の複数行コメント

複素数の絶対値

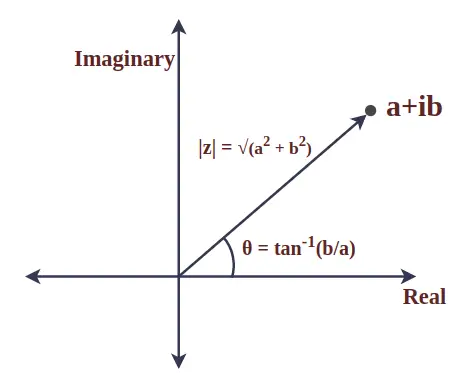
複素数の係数は絶対値であり、原点と指定された点の間の距離を表します。複素数の大きさとしても知られています。複素数 z = a + ib を考えてみましょう。z の係数は次のように定義されます。

|z| = √(a ² +b ² )

どこ、

• ある は複素数 z の実部であり、
• b は複素数 z の虚数部です。

複素数の引数

複素数の動径ベクトルと正の x 軸との間の角度は、複素数の引数と呼ばれます。複素数 z = a + ib の場合、数学的には次のように与えられます。

θ = タン ^-1 (b/a)

どこ、

• ある は複素数 z の実部であり、
• b は複素数 z の虚数部です。

i(イオタ)のパワー

i(iota) は -1 の平方根として定義されます。したがって、i の任意のべき乗は、i 単独の繰り返し乗算として表現できます。

• i = √(-1)
• 私²= -1
• 私³= – 私
• 私⁴= 1
• 私⁵= 私
• 私⁶= – 1
• 等々..

複素数の必要性

古代、人々は自然数について次のような知識しか持っていませんでした。 数字 人間の脳はすでに羊や食べ物などの視覚的なものを使用してそれらを理解しているため、本質的に最も直観的です。したがって、自然数の集合のみが存在します ( N ) しかし、自然数では、方程式 x + a = b (a> b) および a, b ∈ N の解はありません。したがって、自然数の拡張が存在します。つまり、整数( 私 ）。

さて、この一連の数値にも、方程式 ax = b (a ≠ 0) および a, b ∈ I (a と b は両方とも整数) の解はありません。したがって、整数のセット (I) は有理数のセットに拡張されます ( Q ）。

繰り返しますが、この有理数のセットでは、方程式 x の解はありません。²= a (a> 0) および a ∈ Q。したがって、 Q x のような数値を含むように拡張されます。²= a(a> 0の場合)、つまり無理数です。このセットは実数と呼ばれ、次のように表されます。 R 。

さて、この数値の集合は完成しているように見えるため、この実数の集合を拡張して別のより大きな集合を形成する必要はないと長い間考えられてきました。しかし、この数値セットで再び新たな問題が生じます。つまり、x のような実数は存在しません。²= a (a <0) および a ∈ R。したがって、実数のセットは、そのようなすべての値を含むようにさらに拡張され、このセットを複素数と名付け、次のように表されます。 C 。

複素数の分類

ご存知のとおり、複素数の標準形式は次のとおりです。 z = (a + i b) ここで、a、b ∈ R、i は iota (虚数単位) です。したがって、a (実数部と呼ばれる) と b (虚数部と呼ばれる) の値に応じて、複素数は 4 つのタイプに分類されます。

• ゼロ複素数
• 純粋な実数
• 純粋な虚数
• 虚数

これらのタイプについて詳しく学びましょう。

ゼロ複素数

任意の複素数 z = a + ib で、a = 0 & b = 0 の場合、その複素数はゼロ複素数と呼ばれます。たとえば、この唯一の例は 0 です。

純粋な実数

任意の複素数 z = a + ib について、a ≠ 0 & b = 0 の場合、その複素数は純粋な実数、つまり虚数部のない数と呼ばれます。 2、3、5、7 などの実数はすべてこの例です。

純粋な虚数

任意の複素数 z = a + ib について、a = 0 & b ≠ 0 の場合、複素数は純粋な虚数、つまり実部のない数と呼ばれます。実部のないすべての数値 (-7i、-5i、-i、i、5i、7i など) がこのタイプの数値の例です。

虚数

任意の複素数 z = a + ib について、a ≠ 0 & b ≠ 0 の場合、複素数は a と呼ばれます。 虚数 。たとえば、(-1 – i)、(1 + i)、(1 – i)、(2 + 3i) などです。

複素数のさまざまな形式

複素数にはさまざまな形がありますが、

• 長方形のフォルム
• 極形式
• 指数形式

それでは、それらについて詳しく見てみましょう。

長方形のフォルム

長方形のフォルム は とも呼ばれている 標準形式 そしてそれは次のように表されます (a + ib)、a と b は実数です。

例: (5 + 5i)、(-7i)、(-3 – 4i) など。

極形式

極形式 は複素数の表現です。極座標 [座標は (r, θ) として表されます。r は原点からの距離、θ は点と原点を結ぶ線と正の x 軸との間の角度です)。複素数を表すために使用されます。任意の複素数は次のように表されます。 r [cosθ + i sinθ]。

Javaのcomparetoメソッド

例: [cos π/2 + i sin π/2]、5[cos π/6 + i sin π/6] など。

指数形式

複素数の指数形式 はオイラーの公式を使用した複素数の表現であり、この形式では複素数は re で表されます。^私ここで、r は原点からの点の距離、θ は正の x 軸と半径ベクトルの間の角度です。

例:ⁱ⁽⁰⁾、それは^i(π/2)、5.e^i(π/6)、など。

注記： 上で説明した複素数の 3 つの形式はすべて相互変換可能です。つまり、ある形式から別の形式に非常に簡単に変換できます。

複素数の演算

複素数に対して次の操作を実行できます。

• 追加
• 引き算
• 乗算
• 分割
• 活用

複素数の加算

実数部と虚数部を別々に加算するだけで、2 つの複素数を加算できます。

たとえば、(3 + 2i) + (1 + 4i) = 4 + 6i となります。

複素数の引き算

実数部と虚数部を別々に減算するだけで、2 つの複素数を減算できます。

たとえば、(3 + 2i) – (1 + 4i) = 2 – 2i となります。

複素数の乗算

分布特性と i という事実を使用して 2 つの複素数を乗算できます。²= -1。

たとえば、(3 + 2i)(1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i。

複素数の割り算

分子と分母の両方に分母の複素共役を掛けるだけで式をさらに単純化することで、ある複素数を別の複素数で割ることができます。

たとえば、(3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17 となります。

複素数の共役

簡単に見つけることができます 複素数の共役、 虚数部の符号を変更するだけです。複素数の共役は、多くの場合、z̄ のように数値の上にバーで示されます。

たとえば、3 + 2i の共役は 3 – 2i です。

複素数の恒等式

任意の 2 つの複素数 z について₁そしてz₂次の代数恒等式を与えることができます。

• （と ₁ +z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² +2z ₁ ×z ₂
• （と ₁ - と ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2z ₁ ×z ₂
• （と ₁ ) ² - （と ₂ ) ² = (z ₁ +z ₂ ）（と ₁ - と ₂ )
• （と ₁ +z ₂ ) ³ = (z ₁ ) ³ + 3(z ₁ ) ² と ₂ +3(z ₂ ) ² と ₁ + (z ₂ ) ³
• （と ₁ - と ₂ ) ³ = (z ₁ ) ³ – 3(z ₁ ) ² と ₂ +3(z ₂ ) ² と ₁ - （と ₂ ) ³

複素数に関連する公式

複素数に関連する公式がいくつかあります。そのうちのいくつかは次のとおりです。

オイラーの公式

オイラーの公式は、指数の虚数乗と三角比 sin および cos の関係を示し、次の式で与えられます。

それは ^ix = cos x + i sin x

ドゥ・モアブルの公式

ドゥ・モアブルの公式 nを表します^番目極形式の複素数の累乗で、次の式で与えられます。

(cos x + i sin x) ⁿ = cos(nx) + i sin(nx)

複素平面

複素数を一意に表す平面を複素平面、アルガン平面、ガウス平面などと呼びます。

複素平面には 2 つの軸があります。

• X軸または実軸
• Y軸または虚数軸

X軸または実軸

二分探索Python

• すべての純粋な実複素数は、その上の点によって一意に表現されます。
• すべての複素数の実部 Re(z) をそれに関してプロットします。
• そのため、X 軸とも呼ばれます。 実軸 。

Y軸または虚数軸

• すべての純粋な虚数の複素数は、その上の点によって一意に表現されます。
• すべての複素数の虚数部 Im(z) をそれに関してプロットします。
• そのため、Y 軸とも呼ばれます。 虚軸 。

複素数の幾何学的表現

ご存知のとおり、すべての複素数 (z = a + i b) は複素平面上の固有の点 p(a, b) によって表され、複素平面上のすべての点は固有の複素数を表します。

複素数 z = (a + i b) を複素平面上で表すには、次の規則に従います。

• z の実部 (Re(z) = a) が点 p の X 座標になります。

• z の虚数部 (Im(z) = b) が点 p の Y 座標になります。

そして最後に z (a + i b) ⇒ p (a, b) となり、これは複素平面上の点になります。

複素数の性質

複素数にはさまざまなプロパティがあり、その一部を次に示します。

• 任意の複素数 z = a + ib の場合、z = 0 の場合、a = 0 および b = 0 となります。
• 4 つの実数 a、b、c、d について、z₁= a + ib および z₂= c + ID。 zの場合₁= z₂その場合、a = c、b = dとなります。
• 複素数とその共役を加算すると、純粋な実数、つまり z + z̄ = 実数が得られます。

z = a + ib とすると、

z + z̄ = a + 1 + a – 1

⇒ z + z̄ = 2a (これは純粋に実数です)

• 複素数とその共役結果の積も純粋な実数です。つまり、z × z̄ = 実数です。

z = a + ib とすると、

z × z̄ = (a + 1) × (a – 1)

⇒ z × z̄= a²- 私²b²

⇒ z × z̄ = a²+b²（これは純粋に現実です）

• 複素数は 可換 加算と乗算の演算の下で。 2 つの複素数 z を考えてみましょう₁そしてz₂、 その後

と ₁ +z ₂ = z ₂ +z ₁

と ₁ ×z ₂ = z ₂ ×z ₁

• 複素数は 連想的な 加算と乗算の演算を使用します。 3 つの複素数 z を考えてみましょう₁、 と₂、およびz₃それから

（と ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ )

（と ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• 複素数は、 分配財産 足し算よりも掛け算も。 3 つの複素数 z を考えてみましょう₁、 と₂、およびz₃それから

と ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ +z ₁ ×z ₃

続きを読む、

• 複素数の除算
• 複素数の Z バー

複素数の例

例 1: これらの複素数をプロットします z 複素平面上の = 3 + 2i。

解決：

与えられる:

と = 3 + 2 i

したがって、ポイントは z(3, 2) です。この点を下のグラフにプロットします。このグラフでは、x 軸が実数部を表し、y 軸が虚数部を表します。

例 2: これらの複素数をプロットします z ₁ = (2 + 2 i)、z ₂ = (-2 + 3 i)、z ₃ = (-1 – 3 i)、z ₄ = (1 – i) 複素平面上。

解決：

与えられる:

と₁= (2 + 2 i)

と₂= (-2 + 3i)

と₃= (-1 – 3i)

と₄= (1 – i)

したがって、ポイントは z です。₁(2, 2)、z₂(-2、3)、z₃(-1、-3)、および z₄(1、-1)。ここで、これらの点を下のグラフにプロットします。このグラフでは、x 軸が実数部を表し、y 軸が虚数部を表します。

複素数に関する FAQ

複素数を定義します。

a+ib の形式の数値は複素数と呼ばれます。ここで、a と b は実数、i は -1 の平方根を表す虚数単位です。

実数と複素数の違いは何ですか?

実数と複素数の違いは、実数を表すには 1 つの数だけが必要ですが、複素数を表すには 2 つの実数が必要であることです。

複素数の実数部と虚数部は何ですか?

複素数 a + ib では、a は複素数の実数部、b は複素数の虚数部と呼ばれます。

複素数の複素共役とは何ですか?

複素数 a + ib の場合、a – ib はその複素共役と呼ばれます。複素共役は虚数部の符号を変えるだけで求めることができます。

複素数の係数とは何ですか?

原点とアルガンド平面内の複素数で表される点の間の距離は、その完全な数の法と呼ばれ、z = a + ib の場合、数学的に次のように与えられます。

|z| = √(a ² +b ² )

複素数の引数とは何ですか?

複素数の動径ベクトルと正の x 軸の間の角度は複素数の引数と呼ばれ、z = a + ib の場合、数学的には次のように与えられます。

ローマ数字 1 100

θ = タン ^-1 (b/a)

複素数の極形式とは何ですか?

任意の複素数 z = a + ib の場合、その極形式は次の式で与えられます。

r [cosθ + i sinθ]

オイラーの公式とは何ですか?

オイラーの公式は、指数の虚数乗と三角比 sin および cos の関係を示し、次の式で与えられます。

それは ^ix = cos x + i sin x