ローマ数字の起源と使用例 古代ローマ 。今では世界中で使われています。これは、文字と数字が正の数を表すユニークな数値体系です。
ローマ帝国崩壊後も使用は継続されました。すぐに、それに置き換えられました アラビア数字 ;しかし、移行段階は依然として遅いままでした。ローマ数字は時計によく見られます。 1から12までの数字はローマ字で書かれています。
すべてのアルファベットはローマ字として扱われません。 J、U、W を除いて、残りのアルファベットはすべてローマ字として扱われます。
ローマ数字を書くために従う必要があるガイドライン
数字をローマ数字で書くには、いくつかの規則に従う必要があります。ルールの一部を以下に示します。
- シンボルは最大 3 回まで繰り返すことができます。例えば
I、それは -1 を表します。最大 3 回繰り返すことができます (つまり、III)。 - シンボルの値は、シンボルが繰り返されるたびに加算されます。例: 300 - CCC、200 - CC
- ローマ数字体系の一部の記号は繰り返されません。それらの記号は D、L、V です。
- 数値体系には、減算の目的で決して使用されず、より大きな値の記号の前に書かれる記号があります。
- シンボル I はそれぞれ V と X からのみ減算でき、X は L、M、および C からのみ減算できます。
- 小さい値のシンボルが大きい値のシンボルの前にある場合、その値が減算されます。例えば
IX = X - I = 9
一般的なローマ数字

1 - 私
5 - V
10 - ×
50 - 大
Javaでリストを反復する
100 - C
500-D
1000 - M
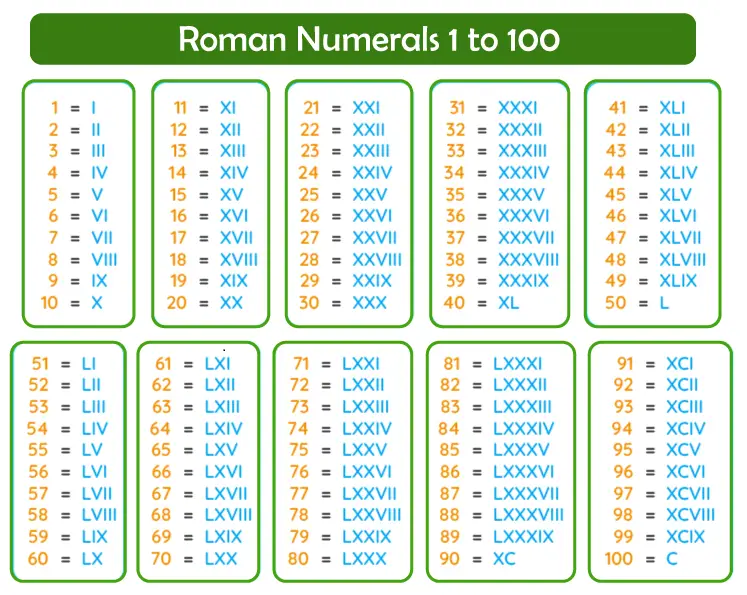
1 から 100 までのローマ数字
1 から 100 までのローマ数字は次のとおりです。
| 番号 | ローマ数字 |
|---|---|
| 1 | 私 |
| 2 | Ⅱ |
| 3 | Ⅲ |
| 4 | Ⅳ |
| 5 | で |
| 6 | 私たちは |
| 7 | Ⅶ |
| 8 | VIII |
| 9 | IX |
| 10 | バツ |
| 十一 | XI |
| 12 | XII |
| 13 | XIII |
| 14 | XIV |
| 15 | XV |
| 16 | XVI |
| 17 | XVII |
| 18 | XVIII |
| 19 | XIX |
| 二十 | XX |
| 21 | XXI |
| 22 | XXII |
| 23 | XXIII |
| 24 | XXIV |
| 25 | XXV |
| 26 | XXVI |
| 27 | XXVII |
| 28 | XXVIII |
| 29 | XXIX |
| 30 | XXX |
| 31 | XXXI |
| 32 | XXXII |
| 33 | XXXIII |
| 3.4 | XXXIV |
| 35 | XXXV |
| 36 | XXXVI |
| 37 | XXXVII |
| 38 | XXXVIII |
| 39 | XXXIX |
| 40 | XL |
| 41 | XLI |
| 42 | XLII |
| 43 | XLIII |
| 44 | XLIV |
| 4つ。 | XLV |
| 46 | XLVI |
| 47 | XLVII |
| 48 | 48 |
| 49 | 第49回 |
| 50 | L |
| 51 | それ |
| 52 | LⅡ |
| 53 | LⅡ |
| 54 | 人生 |
| 55 | LV |
| 56 | LVI |
| 57 | LVII |
| 58 | LVIII |
| 59 | 六 |
| 60 | LX |
| 61 | LXI |
| 62 | LXII |
| 63 | LXIII |
| 64 | LXIV |
| 65 | 65 |
| 66 | LXVI |
| 67 | 67 |
| 68 | 68 |
| 69 | 69 |
| 70 | LXX |
| 71 | 71 |
| 72 | 72 |
| 73 | 73 |
| 74 | 74 |
| 75 | 75 |
| 76 | 76 |
| 77 | 77 |
| 78 | 78 |
| 79 | 79 |
| 80 | 80 |
| 81 | 81 |
| 82 | 82 |
| 83 | 833 |
| 84 | 84 |
| 85 | 85 |
| 86 | 86 |
| 87 | 87 |
| 88 | 88 |
| 89 | 89 |
| 90 | XC |
| 91 | XCI |
| 92 | XXII |
| 93 | XCIII |
| 94 | 94 |
| 95 | XCV |
| 96 | 96 |
| 97 | 97 |
| 98 | 98 |
| 99 | 99 |
| 100 | C |
ローマ数字から数字への変換
ルール 1: 金額を加算するよりも大きな値の文字の後に 1 つ以上の記号が配置されている場合、
- 8 = 8 (5 + 3)
- LXX = 70 (50 + 10 + 10)
- MCC = 1200 (1000 + 100 +100)
ルール 2: 記号がより大きな値の別の文字の前に配置されている場合は、その量を減算します。
IX = 9 (10 - 1= 9)
CCM = 800 (1000-100-100 = 800)
解決済みの例
問題: 78 をローマ数字で書きなさい
解: 78 = 70 + 8
= (50 + 20) (10 - 2)
= 70 + 8
= 78
したがって、78 = 78
問題: 3575 をローマ数字で書きなさい
答え: 3000、500、70、5 に分類される 4 桁の数字です。
3575= 3000 + 500 + 70 + 5
それで
5 = V
70 = LXX
500 = D
3000 = MMM
3575 = MMM+D+LXX+V
= MMMDLXXV
質問: 次の質問の答えを決めてください
1) 80
年: = 50 + 30
= 80
2) C + LX
年: = 100 + 60
= 160
3) 122 - 80 - 52
年: MXXII
= M + 20 + II
= 1000 + 20 + 2
= 1022
LXX
Wordの透かし
= L +XXX
= 50 + 30
= 80
LⅡ
= L + II
= 50 + 2
= 52
= 1022-80-52
= 1022-132
= 890
4) MMM+LLL+XX
年: うーん
= 1000 + 1000 + 1000
= 3000
LLL
= 50 + 50 + 50
= 150
XX
= 10 + 10
= 20
= 3000 + 150 + 20
= 3170
