NFA では、指定された入力シンボルの指定された状態からゼロ、1 つ、または複数の移動を行うことができます。 NFA には NULL 移動 (入力シンボルなしの移動) も含めることができます。一方、DFA では、指定された入力シンボルの指定された状態からの移動は 1 つだけです。
itn への文字列
NFA を DFA に変換する手順:
ステップ 1: 指定された NFA を同等の遷移テーブルに変換する
NFA を同等の遷移テーブルに変換するには、すべての状態、入力シンボル、および遷移ルールをリストする必要があります。遷移ルールは行列の形式で表されます。行は現在の状態を表し、列は入力シンボルを表し、セルは次の状態を表します。
ステップ 2: DFA の開始状態を作成する
DFA の開始状態は、NFA で可能なすべての開始状態のセットです。このセットは、NFA の開始状態のイプシロン閉包と呼ばれます。イプシロン クロージャは、イプシロン (?) 遷移をたどることによって開始状態から到達できるすべての状態のセットです。
ステップ 3: DFA の遷移テーブルを作成する
DFA の遷移テーブルは NFA の遷移テーブルに似ていますが、個々の状態ではなく、行と列が状態のセットを表します。各入力シンボルについて、遷移テーブルの対応するセルには、NFA の遷移テーブルの遷移ルールに従って取得された状態セットのイプシロン閉包が含まれています。
ステップ 4: DFA の最終状態を作成する
DFA の最終状態は、NFA からの最終状態を少なくとも 1 つ含む状態のセットです。
ステップ 5: DFA を簡素化する
前の手順で取得した DFA には、不要な状態や遷移が含まれている可能性があります。 DFA を簡素化するには、次の手法を使用できます。
- 到達不能な状態を削除する: 開始状態から到達できない状態は、DFA から削除できます。
- デッド ステートの削除: 最終状態に至らないステートは DFA から削除できます。
- 同等の状態をマージ: すべての入力シンボルに対して同じ遷移ルールを持つ状態を 1 つの状態にマージできます。
ステップ 6: これ以上単純化できなくなるまでステップ 3 ~ 5 を繰り返します。
DFA を単純化した後、これ以上単純化できなくなるまでステップ 3 ~ 5 を繰り返します。得られる最終的な DFA は、指定された NFA に相当する最小化された DFA です。
例: 図 1 に示す次の NFA について考えてみましょう。
PowerShell の複数行コメント

以下は、NFA のさまざまなパラメーターです。 Q = { q0, q1, q2 } ? = ( a, b ) F = { q2 } ? (NFAの遷移関数)
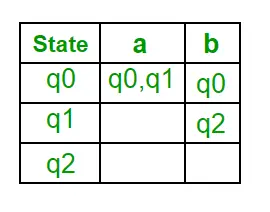
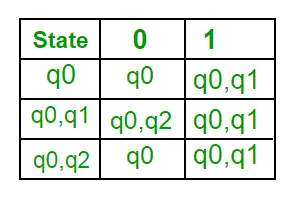
ステップ 1: Q’ = ?ステップ 2: Q' = {q0} ステップ 3: Q' の各状態について、各入力シンボルの状態を見つけます。現在、Q’ の状態は q0 であり、NFA の遷移関数を使用して入力シンボル a および b 上で q0 からの移動を見つけ、DFA の遷移テーブルを更新します。 ?’ (DFAの遷移関数)

ここで、{ q0, q1 } は単一の状態と見なされます。 Q’にエントリがないのでQ’に追加します。したがって、Q' = { q0, { q0, q1 } } ここで、異なる入力シンボルでの状態 { q0, q1 } からの移動は DFA の遷移テーブルに存在しないため、次のように計算します。 、a) = ? ( q0, a ) ? ? ( q1, a ) = { q0, q1 } ?’ ( { q0, q1 }, b ) = ? ( q0, b ) ? ? ( q1, b ) = { q0, q2 } 次に、DFA の遷移テーブルを更新します。 ?’ (DFAの遷移関数)
クリック時のjQuery

ここで、{ q0, q2 } は単一の状態と見なされます。 Q’にエントリがないのでQ’に追加します。したがって、Q' = { q0, { q0, q1 }, { q0, q2 } } ここで、異なる入力シンボルでの状態 {q0, q2} からの移動は DFA の遷移テーブルに存在しないため、次のように計算します。 ( { q0 , q2 }, a ) = ? ( q0, a ) ? ? ( q2, a ) = { q0, q1 } ?’ ( { q0, q2 }, b ) = ? ( q0, b ) ? ? ( q2, b ) = { q0 } 次に、DFA の遷移テーブルを更新します。 ?’ (DFAの遷移関数)
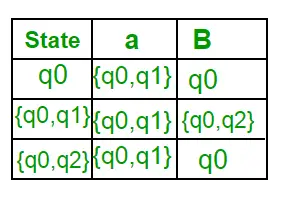
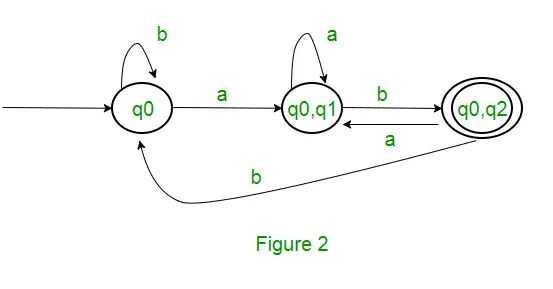
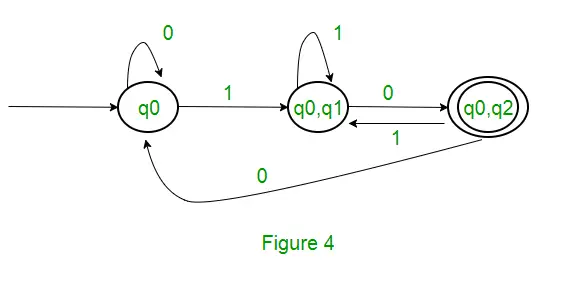
新しい状態は生成されないため、変換は完了です。 DFA の最終状態は、コンポーネントとして q2 を持つ状態、つまり { q0, q2 } になります。 以下は、DFA のさまざまなパラメーターです。 Q’ = { q0, { q0, q1 }, { q0, q2 } } ? = ( a, b ) F = { { q0, q2 } } および遷移関数 ?’ を上に示します。上記の NFA の最終的な DFA を図 2 に示します。
注記 : 場合によっては、正規表現を DFA に変換するのが簡単ではないことがあります。まず正規表現を NFA に変換し、次に NFA を DFA に変換できます。
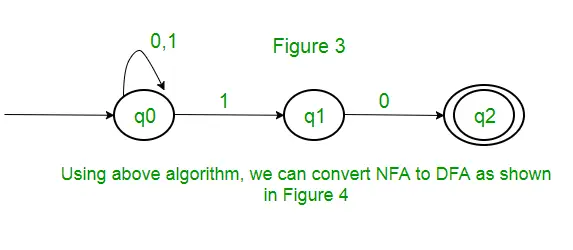
質問 : 正規表現 (0 + 1)* (10) に対応する最小決定論的有限オートマトンの状態の数は ____________ です。
解決 : まず、上記の式に対して NFA を作成します。 (0 + 1)* の NFA を作成するには、NFA は入力シンボル 0 または 1 で同じ状態 q0 になります。次に、連結のために、図に示すように 2 つの移動 (1 の場合は q0 から q1 へ、0 の場合は q1 から q2 へ) を追加します。図 3 にあります。
配列ソートJava
この記事は Sonal Tuteja によって寄稿されました。
