- DFA は決定論的有限オートマトンを指します。決定性とは、計算の一意性を指します。マシンが入力文字列を一度に 1 シンボルずつ読み取る場合、有限オートマトンは決定論的有限オートマトンと呼ばれます。
- DFA では、現在の状態から次の状態への特定の入力のパスは 1 つだけです。
- DFA は null 移動を受け入れません。つまり、DFA は入力文字なしでは状態を変更できません。
- DFA には複数の最終状態を含めることができます。コンパイラの字句解析で使用されます。
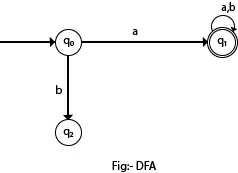
次の図では、入力 a の状態 q0 から、q1 に向かうパスが 1 つだけ存在することがわかります。同様に、q0 から q2 に向かう入力 b のパスは 1 つだけです。
DFA の正式な定義
DFA は、FA の定義で説明したのと同じ 5 タプルのコレクションです。
カット・ティンフの妹
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
遷移関数は次のように定義できます。
δ: Q x ∑→Q
DFA のグラフィック表現
DFA は、状態図と呼ばれる有向グラフで表すことができます。その中で:
- 状態は頂点によって表されます。
- 入力文字のラベルが付いた円弧は遷移を示します。
- 初期状態は矢印でマークされています。
- 最終状態は二重丸で示される。
例 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} 解決:
遷移図:

遷移表:
| 現状 | 入力 0 の次の状態 | 入力 1 の次の状態 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
例 2:
∑ = {0, 1} の DFA は、0 で始まるすべてを受け入れます。
解決:

説明:
ベースバンドとブロードバンド
- 上の図では、状態 q0 の DFA への入力として 0 が与えられると、DFA は状態を q1 に変更し、入力 0 を開始すると常に最終状態 q1 に進むことがわかります。00、01、000、001... を受け入れることができます。 。等。 1 で始まる文字列では最終状態に移行しないため、1 で始まる文字列は受け入れられません。
例 3:
∑ = {0, 1} の DFA は、0 で終わるすべてを受け入れます。
解決:

説明:
上の図では、状態 q0 の DFA への入力として 0 が与えられると、DFA は状態を q1 に変更することがわかります。 00、10、110、100.... など、0 で終わる任意の文字列を受け入れることができます。 1 で終わる文字列は受け入れられません。1 つの入力で最終状態 q1 には決してならないため、1 で終わる文字列は受け入れられないか、拒否されます。
