最初に空のセットがあり、それに対するいくつかのクエリが与えられた場合、それぞれ次のタイプの可能性があります。
- 「x」の挿入は、update(1 0 10^6 x 1) を使用して行われます。 x を持つすべての範囲が更新されるように、ツリーのルートには開始インデックスが 0 として渡され、終了インデックスが 10^6 として渡されることに注意してください。
- 「x」の削除は、update(1 0 10^6 x -1) を使用して行われます。 x を持つすべての範囲が更新されるように、ツリーのルートには開始インデックスが 0 として渡され、終了インデックスが 10^6 として渡されることに注意してください。
例:
Input : Insert 1 Insert 4 Insert 7 Median Output : The first three queries should insert 1 4 and 7 into an empty set. The fourth query should return 4 (median of 1 4 7).
説明の目的で次のことを仮定しますが、これらの仮定はここで説明する方法の制限ではありません。
1. どのような場合でも、すべての要素は個別です。つまり、どの要素も複数回出現しません。
2. 「中央値」クエリは、セット内に奇数の要素がある場合にのみ作成されます。(偶数の場合、セグメント ツリーで 2 つのクエリを作成する必要があります)。
3. セット内の要素の範囲は 1 ~ +10^6 です。
方法 1 (ナイーブ)
単純な実装では、最初の 2 つのクエリは O(1) で実行できますが、最後のクエリは O(max_elem) で実行できます。ここで、max_elem はすべての時点の最大要素 (削除された要素を含む) です。
配列を想定してみましょう カウント[] (サイズ 10^6 + 1) を使用して、サブセット内の各要素の数を維持します。以下は、3 つのクエリの単純で説明不要のアルゴリズムです。
x クエリを挿入します。
count[x]++; if (x > max_elem) max_elem = x; n++;
x クエリを削除:
if (count[x] > 0) count[x]--; n--;
中央値クエリ:
sum = 0; i = 0; while( sum <= n / 2 ) { i++; sum += count[i]; } median = i; return median; 集合 {1 4 7 8 9} を表す配列 count[] の図、中央値の要素は「7」です。

「中央値」クエリは、配列内の (n + 1)/2 番目の「1」、この場合は 3 番目の「1」を見つけることを目的としています。次に、セグメント ツリーを使用して同じことを行います。
方法2(使用方法) セグメントツリー )
私たちは、 セグメントツリー 間隔の合計を格納します。間隔 [a b] は、現在範囲 [a b] 内にあるセット内に存在する要素の数を表します。たとえば、上記の例を考えると、 query(3 7) は 2 を返します。 query(4 4) は 1 を返します。 query(5 5) は 0 を返します。
挿入クエリと削除クエリは単純で、両方とも関数 update(int x int diff) を使用して実装できます (インデックス 'x' に 'diff' を追加します)
アルゴリズム
// adds ‘diff’ at index ‘x’ update(node a b x diff) // If leaf node If a == b and a == x segmentTree[node] += diff // If non-leaf node and x lies in its range If x is in [a b] // Update children recursively update(2*node a (a + b)/2 x diff) update(2*node + 1 (a + b)/2 + 1 b x diff) // Update node segmentTree[node] = segmentTree[2 * node] + segmentTree[2 * node + 1]
上記の再帰関数は以下で実行されます。 O( log( max_elem ) ) (この場合、max_elem は 10^6)、次の呼び出しで挿入と削除の両方に使用されます。
さて、k 番目の「1」を持つインデックスを見つける関数です。この場合の「k」は常に (n + 1) / 2 になります。これは二分探索とよく似た働きをします。セグメント ツリー上の再帰二分探索関数と考えることができます。
例を挙げて、セットには現在要素 { 1 4 7 8 9 } があり、したがって次のセグメント ツリーで表されることを理解しましょう。
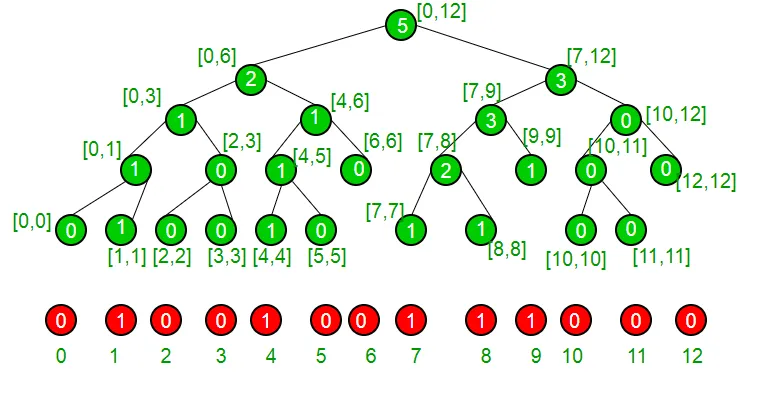
非リーフノードにいる場合、両方の子があることを確信します。左の子が「k」以上の 1 を持っているかどうかを確認します。はいの場合、インデックスは左のサブツリーにあると確信します。そうでない場合、左のサブツリーの 1 の数が k よりも少ない場合、インデックスは右のサブツリーにあると確信します。これを再帰的に実行してインデックスに到達し、そこからインデックスを返します。
アルゴリズム
1.findKth(node a b k) 2. If a != b 3. If segmentTree[ 2 * node ] >= k 4. return findKth(2*node a (a + b)/2 k) 5. else 6. return findKth(2*node + 1 (a + b)/2 + 1 b k - segmentTree[ 2 * node ]) 7. else 8. return a
上記の再帰関数は以下で実行されます。 O( log(max_elem) ) 。
// A C++ program to implement insert delete and // median queries using segment tree #include
// A Java program to implement insert delete and // median queries using segment tree import java.io.*; class GFG{ public static int maxn = 3000005; public static int max_elem = 1000000; // A global array to store segment tree. // Note: Since it is global all elements are 0. public static int[] segmentTree = new int[maxn]; // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. public static void update(int node int a int b int x int diff) { // If current node is a leaf node if (a == b && a == x ) { // Add 'diff' and return segmentTree[node] += diff; return ; } // If current node is non-leaf and 'x' // is in its range if (x >= a && x <= b) { // Update both sub-trees left and right update(node * 2 a (a + b) / 2 x diff); update(node * 2 + 1 (a + b) / 2 + 1 b x diff); // Finally update current node segmentTree[node] = segmentTree[node * 2] + segmentTree[node * 2 + 1]; } } // Returns k'th node in segment tree public static int findKth(int node int a int b int k) { // Non-leaf node will definitely have both // children; left and right if (a != b) { // If kth element lies in the left subtree if (segmentTree[node * 2] >= k) { return findKth(node * 2 a (a + b) / 2 k); } // If kth one lies in the right subtree return findKth(node * 2 + 1 (a + b) / 2 + 1 b k - segmentTree[node * 2]); } // If at a leaf node return the index it stores // information about return (segmentTree[node] != 0) ? a : -1; } // Insert x in the set public static void insert(int x) { update(1 0 max_elem x 1); } // Delete x from the set public static void delete(int x) { update(1 0 max_elem x -1); } // Returns median element of the set // with odd cardinality only public static int median() { int k = (segmentTree[1] + 1) / 2; return findKth(1 0 max_elem k); } // Driver code public static void main(String[] args) { insert(1); insert(4); insert(7); System.out.println('Median for the set {147} = ' + median()); insert(8); insert(9); System.out.println('Median for the set {14789} = ' + median()); delete(1); delete(8); System.out.println('Median for the set {479} = ' + median()); } } // This code is contributed by avanitrachhadiya2155
# A Python3 program to implement insert delete and # median queries using segment tree maxn = 3000005 max_elem = 1000000 # A global array to store segment tree. # Note: Since it is global all elements are 0. segmentTree = [0 for i in range(maxn)] # Update 'node' and its children in segment tree. # Here 'node' is index in segmentTree[] 'a' and # 'b' are starting and ending indexes of range stored # in current node. # 'diff' is the value to be added to value 'x'. def update(node a b x diff): global segmentTree # If current node is a leaf node if (a == b and a == x ): # add 'diff' and return segmentTree[node] += diff return # If current node is non-leaf and 'x' is in its # range if (x >= a and x <= b): # update both sub-trees left and right update(node * 2 a (a + b)//2 x diff) update(node * 2 + 1 (a + b)//2 + 1 b x diff) # Finally update current node segmentTree[node] = segmentTree[node * 2] + segmentTree[node * 2 + 1] # Returns k'th node in segment tree def findKth(node a b k): global segmentTree # non-leaf node will definitely have both # children left and right if (a != b): # If kth element lies in the left subtree if (segmentTree[node * 2] >= k): return findKth(node * 2 a (a + b)//2 k) # If kth one lies in the right subtree return findKth(node * 2 + 1 (a + b)//2 + 1 b k - segmentTree[node * 2]) # if at a leaf node return the index it stores # information about return a if (segmentTree[node]) else -1 # insert x in the set def insert(x): update(1 0 max_elem x 1) # delete x from the set def delete(x): update(1 0 max_elem x -1) # returns median element of the set with odd # cardinality only def median(): k = (segmentTree[1] + 1) // 2 return findKth(1 0 max_elem k) # Driver code if __name__ == '__main__': insert(1) insert(4) insert(7) print('Median for the set {147} ='median()) insert(8) insert(9) print('Median for the set {14789} ='median()) delete(1) delete(8) print('Median for the set {479} ='median()) # This code is contributed by mohit kumar 29
// A C# program to implement insert delete // and median queries using segment tree using System; class GFG{ public static int maxn = 3000005; public static int max_elem = 1000000; // A global array to store segment tree. // Note: Since it is global all elements are 0. public static int[] segmentTree = new int[maxn]; // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. public static void update(int node int a int b int x int diff) { // If current node is a leaf node if (a == b && a == x) { // Add 'diff' and return segmentTree[node] += diff; return ; } // If current node is non-leaf and 'x' // is in its range if (x >= a && x <= b) { // Update both sub-trees left and right update(node * 2 a (a + b) / 2 x diff); update(node * 2 + 1 (a + b) / 2 + 1 b x diff); // Finally update current node segmentTree[node] = segmentTree[node * 2] + segmentTree[node * 2 + 1]; } } // Returns k'th node in segment tree public static int findKth(int node int a int b int k) { // Non-leaf node will definitely have both // children; left and right if (a != b) { // If kth element lies in the left subtree if (segmentTree[node * 2] >= k) { return findKth(node * 2 a (a + b) / 2 k); } // If kth one lies in the right subtree return findKth(node * 2 + 1 (a + b) / 2 + 1 b k - segmentTree[node * 2]); } // If at a leaf node return the index it // stores information about if (segmentTree[node] != 0) { return a; } else { return -1; } } // Insert x in the set public static void insert(int x) { update(1 0 max_elem x 1); } // Delete x from the set public static void delete(int x) { update(1 0 max_elem x -1); } // Returns median element of the set // with odd cardinality only public static int median() { int k = (segmentTree[1] + 1) / 2; return findKth(1 0 max_elem k); } // Driver code static public void Main() { insert(1); insert(4); insert(7); Console.WriteLine('Median for the set {147} = ' + median()); insert(8); insert(9); Console.WriteLine('Median for the set {14789} = ' + median()); delete(1); delete(8); Console.WriteLine('Median for the set {479} = ' + median()); } } // This code is contributed by rag2127
<script> // A Javascript program to implement insert delete and // median queries using segment tree let maxn = 3000005; let max_elem = 1000000; // A global array to store segment tree. // Note: Since it is global all elements are 0. let segmentTree = new Array(maxn); for(let i=0;i<maxn;i++) { segmentTree[i]=0; } // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. function update(nodeabxdiff) { // If current node is a leaf node if (a == b && a == x ) { // Add 'diff' and return segmentTree[node] += diff; return ; } // If current node is non-leaf and 'x' // is in its range if (x >= a && x <= b) { // Update both sub-trees left and right update(node * 2 a Math.floor((a + b) / 2) x diff); update(node * 2 + 1 Math.floor((a + b) / 2) + 1 b x diff); // Finally update current node segmentTree[node] = segmentTree[node * 2] + segmentTree[node * 2 + 1]; } } // Returns k'th node in segment tree function findKth(nodeabk) { // Non-leaf node will definitely have both // children; left and right if (a != b) { // If kth element lies in the left subtree if (segmentTree[node * 2] >= k) { return findKth(node * 2 a Math.floor((a + b) / 2) k); } // If kth one lies in the right subtree return findKth(node * 2 + 1 Math.floor((a + b) / 2) + 1 b k - segmentTree[node * 2]); } // If at a leaf node return the index it stores // information about return (segmentTree[node] != 0) ? a : -1; } // Insert x in the set function insert(x) { update(1 0 max_elem x 1); } // Delete x from the set function delet(x) { update(1 0 max_elem x -1); } // Returns median element of the set // with odd cardinality only function median() { let k = (segmentTree[1] + 1) / 2; return findKth(1 0 max_elem k); } // Driver code insert(1); insert(4); insert(7); document.write('Median for the set {147} = ' + median()+'
'); insert(8); insert(9); document.write('Median for the set {14789} = ' + median()+'
'); delet(1); delet(8); document.write('Median for the set {479} = ' + median()+'
'); // This code is contributed by unknown2108 </script>
出力:
Median for the set {147} = 4 Median for the set {14789} = 7 Median for the set {479} = 7
結論:
3 つのクエリすべてが実行されます O( log(max_elem) ) この場合、max_elem = 10^6 なので、log(max_elem) はほぼ 20 に等しくなります。
セグメントツリーは以下を使用します O( max_elem ) 空間。
削除クエリが存在しなかった場合、この問題は有名なアルゴリズムでも解決できた可能性があります。 ここ 。
