ユークリッド アルゴリズムは、2 つの正の整数の最大公約数を見つける方法です。 2 つの数値の GCD は、両方を除算する最大の数です。 GCD を求める簡単な方法は、両方の数値を因数分解し、共通の素因数を乗算することです。
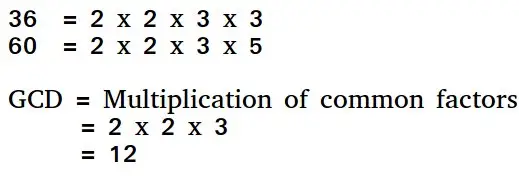
GCD の基本的なユークリッド アルゴリズム:
このアルゴリズムは以下の事実に基づいています。
- 大きい数から小さい数を引いても (大きい数を減らしても)、GCD は変わりません。したがって、2 のうち大きい方を繰り返し減算し続けると、最終的に GCD が得られます。
- 減算の代わりに、小さい方の数値を除算すると、余りが 0 になった時点でアルゴリズムが停止します。
以下は、Euclid のアルゴリズムを使用して gcd を評価する再帰関数です。
C
// C program to demonstrate Basic Euclidean Algorithm> #include> // Function to return gcd of a and b> int> gcd(>int> a,>int> b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver code> int> main()> {> >int> a = 10, b = 15;> > >// Function call> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >a = 35, b = 10;> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >a = 31, b = 2;> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >return> 0;> }> |
>
>
CPP
// C++ program to demonstrate> // Basic Euclidean Algorithm> #include> using> namespace> std;> // Function to return> // gcd of a and b> int> gcd(>int> a,>int> b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver Code> int> main()> {> >int> a = 10, b = 15;> > >// Function call> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >a = 35, b = 10;> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >a = 31, b = 2;> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >return> 0;> }> |
>
32 ビット アーキテクチャと 64 ビット アーキテクチャ
>
ジャワ
// Java program to demonstrate Basic Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> >// extended Euclidean Algorithm> >public> static> int> gcd(>int> a,>int> b)> >{> >if> (a ==>0>)> >return> b;> >return> gcd(b % a, a);> >}> >// Driver code> >public> static> void> main(String[] args)> >{> >int> a =>10>, b =>15>, g;> > >// Function call> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a =>35>;> >b =>10>;> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a =>31>;> >b =>2>;> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >}> }> // Code Contributed by Mohit Gupta_OMG> |
>
>
Python3
# Python3 program to demonstrate Basic Euclidean Algorithm> # Function to return gcd of a and b> def> gcd(a, b):> >if> a>=>=> 0>:> >return> b> >return> gcd(b>%> a, a)> # Driver code> if> __name__>=>=> '__main__'>:> >a>=> 10> >b>=> 15> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> >a>=> 35> >b>=> 10> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> >a>=> 31> >b>=> 2> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> # Code Contributed By Mohit Gupta_OMG> |
>
>
C#
// C# program to demonstrate Basic Euclidean Algorithm> using> System;> class> GFG {> >public> static> int> gcd(>int> a,>int> b)> >{> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> >}> >// Driver Code> >static> public> void> Main()> >{> >int> a = 10, b = 15, g;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a = 35;> >b = 10;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a = 31;> >b = 2;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >}> }> // This code is contributed by ajit> |
>
>
PHP
// php program to demonstrate Basic Euclidean Algorithm> // PHP program to demonstrate // Basic Euclidean Algorithm // Function to return // gcd of a and b function gcd($a, $b) { if ($a == 0) return $b; return gcd($b % $a, $a); } // Driver Code $a = 10; $b = 15; // Function call echo 'GCD(',$a,',' , $b,') = ', gcd($a, $b); echo '
'; $a = 35; $b = 10; echo 'GCD(',$a ,',',$b,') = ', gcd($a, $b); echo '
'; $a = 31; $b = 2; echo 'GCD(',$a ,',', $b,') = ', gcd($a, $b); // This code is contributed by m_kit ?>>> |
>
>
JavaScript
// JavaScript program to demonstrate> // Basic Euclidean Algorithm> // Function to return> // gcd of a and b> function> gcd( a, b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver Code> >let a = 10, b = 15;> >document.write(>'GCD('> + a +>', '> >+ b +>') = '> + gcd(a, b) +>' '>);> > >a = 35, b = 10;> >document.write(>'GCD('> + a +>', '> >+ b +>') = '> + gcd(a, b) +>' '>);> > >a = 31, b = 2;> >document.write(>'GCD('> + a +>', '> >+ b +>') = '> + gcd(a, b) +>' '>);> // This code contributed by aashish1995> |
>
>出力
GCD(10, 15) = 5 GCD(35, 10) = 5 GCD(31, 2) = 1>
時間計算量: O(ログ最小(a, b))
補助スペース: O(Log (min(a,b))
拡張ユークリッド アルゴリズム:
拡張ユークリッド アルゴリズムでは、次のような整数係数 x および y も検索されます。 ax + by = gcd(a, b)
例:
入力: a = 30、b = 20
出力: gcd = 10、x = 1、y = -1
(30*1 + 20*(-1) = 10 であることに注意してください)入力: a = 35、b = 15
出力: gcd = 5、x = 1、y = -2
(35*1 + 15*(-2) = 5 であることに注意してください)
拡張ユークリッド アルゴリズムは、再帰呼び出し gcd(b%a, a) によって計算された結果を使用して、gcd(a, b) の結果を更新します。再帰呼び出しで計算されたxとyの値をxとする1そしてy1。 x と y は以下の式を使用して更新されます。
推奨演習 拡張ユークリッド アルゴリズム 試してみましょう!ax + by = gcd(a, b)
gcd(a, b) = gcd(b%a, a)
gcd(b%a, a) = (b%a)x1+は1
ax + by = (b%a)x1+は1
ax + by = (b – [b/a] * a)x1+は1
ax + by = a(y1– [b/a] * x1) + bx1左側と右側を比較すると、
x = y1– ?b/a? * バツ1
y = x1
以下は上記のアプローチの実装です。
C++
// C++ program to demonstrate working of> // extended Euclidean Algorithm> #include> using> namespace> std;> // Function for extended Euclidean Algorithm> int> gcdExtended(>int> a,>int> b,>int> *x,>int> *y)> {> >// Base Case> >if> (a == 0)> >{> >*x = 0;> >*y = 1;> >return> b;> >}> >int> x1, y1;>// To store results of recursive call> >int> gcd = gcdExtended(b%a, a, &x1, &y1);> >// Update x and y using results of> >// recursive call> >*x = y1 - (b/a) * x1;> >*y = x1;> >return> gcd;> }> // Driver Code> int> main()> {> >int> x, y, a = 35, b = 15;> >int> g = gcdExtended(a, b, &x, &y);> >cout <<>'GCD('> << a <<>', '> << b> ><<>') = '> << g << endl;> >return> 0;> }> |
CSSトランジションの不透明度
>
>
C
// C program to demonstrate working of extended> // Euclidean Algorithm> #include> // C function for extended Euclidean Algorithm> int> gcdExtended(>int> a,>int> b,>int> *x,>int> *y)> {> >// Base Case> >if> (a == 0)> >{> >*x = 0;> >*y = 1;> >return> b;> >}> >int> x1, y1;>// To store results of recursive call> >int> gcd = gcdExtended(b%a, a, &x1, &y1);> >// Update x and y using results of recursive> >// call> >*x = y1 - (b/a) * x1;> >*y = x1;> >return> gcd;> }> // Driver Program> int> main()> {> >int> x, y;> >int> a = 35, b = 15;> >int> g = gcdExtended(a, b, &x, &y);> >printf>(>'gcd(%d, %d) = %d'>, a, b, g);> >return> 0;> }> |
>
>
ジャワ
// Java program to demonstrate working of extended> // Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> >// extended Euclidean Algorithm> >public> static> int> gcdExtended(>int> a,>int> b,>int> x,> >int> y)> >{> >// Base Case> >if> (a ==>0>) {> >x =>0>;> >y =>1>;> >return> b;> >}> >int> x1 =>1>,> >y1 =>1>;>// To store results of recursive call> >int> gcd = gcdExtended(b % a, a, x1, y1);> >// Update x and y using results of recursive> >// call> >x = y1 - (b / a) * x1;> >y = x1;> >return> gcd;> >}> >// Driver Program> >public> static> void> main(String[] args)> >{> >int> x =>1>, y =>1>;> >int> a =>35>, b =>15>;> >int> g = gcdExtended(a, b, x, y);> >System.out.print(>'gcd('> + a +>' , '> + b> >+>') = '> + g);> >}> }> |
watchcartoononline.ioの代替案
>
>
Python3
# Python program to demonstrate working of extended> # Euclidean Algorithm> # function for extended Euclidean Algorithm> def> gcdExtended(a, b):> ># Base Case> >if> a>=>=> 0>:> >return> b,>0>,>1> >gcd, x1, y1>=> gcdExtended(b>%> a, a)> ># Update x and y using results of recursive> ># call> >x>=> y1>-> (b>/>/>a)>*> x1> >y>=> x1> >return> gcd, x, y> # Driver code> a, b>=> 35>,>15> g, x, y>=> gcdExtended(a, b)> print>(>'gcd('>, a,>','>, b,>') = '>, g)> |
>
>
C#
// C# program to demonstrate working> // of extended Euclidean Algorithm> using> System;> class> GFG> {> > >// extended Euclidean Algorithm> >public> static> int> gcdExtended(>int> a,>int> b,> >int> x,>int> y)> >{> >// Base Case> >if> (a == 0)> >{> >x = 0;> >y = 1;> >return> b;> >}> >// To store results of> >// recursive call> >int> x1 = 1, y1 = 1;> >int> gcd = gcdExtended(b % a, a, x1, y1);> >// Update x and y using> >// results of recursive call> >x = y1 - (b / a) * x1;> >y = x1;> >return> gcd;> >}> > >// Driver Code> >static> public> void> Main ()> >{> >int> x = 1, y = 1;> >int> a = 35, b = 15;> >int> g = gcdExtended(a, b, x, y);> >Console.WriteLine(>'gcd('> + a +>' , '> +> >b +>') = '> + g);> >}> }> |
>
>
PHP
// PHP program to demonstrate // working of extended // Euclidean Algorithm // PHP function for // extended Euclidean // Algorithm function gcdExtended($a, $b, $x, $y) { // Base Case if ($a == 0) { $x = 0; $y = 1; return $b; } // To store results // of recursive call $gcd = gcdExtended($b % $a, $a, $x, $y); // Update x and y using // results of recursive // call $x = $y - floor($b / $a) * $x; $y = $x; return $gcd; } // Driver Code $x = 0; $y = 0; $a = 35; $b = 15; $g = gcdExtended($a, $b, $x, $y); echo 'gcd(',$a; echo ', ' , $b, ')'; echo ' = ' , $g; ?>>> |
>
>
JavaScript
> // Javascript program to demonstrate> // working of extended> // Euclidean Algorithm> // Javascript function for> // extended Euclidean> // Algorithm> function> gcdExtended(a, b,> >x, y)> {> >// Base Case> >if> (a == 0)> >{> >x = 0;> >y = 1;> >return> b;> >}> >// To store results> >// of recursive call> >let gcd = gcdExtended(b % a,> >a, x, y);> >// Update x and y using> >// results of recursive> >// call> >x = y - (b / a) * x;> >y = x;> >return> gcd;> }> // Driver Code> let x = 0;> let y = 0;> let a = 35;> let b = 15;> let g = gcdExtended(a, b, x, y);> document.write(>'gcd('> + a);> document.write(>', '> + b +>')'>);> document.write(>' = '> + g);> > |
>
>
出力:
gcd(35, 15) = 5>
時間計算量: O(log N)
補助スペース: O(log N)
拡張アルゴリズムはどのように機能するのでしょうか?
上で見たように、x と y は入力 a と b の結果です。
a.x + b.y = gcd —-(1)
そして×1そしてy1入力 b%a および a の結果です
(b%a).x1+ああ1= gcd
上記に b%a = (b – (?b/a?).a) を代入すると、
フォローを取得します。 ?b/a? に注意してください。床(b/a)です(b – (?b/a?).a).x1+ああ1= gcd
上式は次のように書くこともできます
b.x1+ a.(そして1– (?b/a?).x1) = gcd —(2)
(1)の「a」と「b」の係数を比較した後、
(2) を実行すると、次のようになります。
x = y1– ?b/a? * バツ1
y = x1
拡張アルゴリズムはどのように役立ちますか?
拡張ユークリッド アルゴリズムは、a と b が互いに素である (または gcd が 1) 場合に特に役立ちます。 x は b を法とする a の逆剰余であり、y は a を法とする b の逆剰余であるためです。特に、モジュラ乗算逆元の計算は、RSA 公開キー暗号化方式において重要なステップです。
