三角錐の公式

三角錐の体積は次の式で求められます。 V = 1/3A.H 。四面体としても知られる三角錐は、三角形の底面と、頂点と呼ばれる 1 点で交わる 3 つの三角形の面を持つピラミッドの一種です。

この記事では、ピラミッドの定義、三角錐の定義、三角錐の公式、例などについて詳しく学びます。

ピラミッドとは何ですか?
三角錐の定義
三角錐の公式
三角錐の表面積
三角錐の体積

ピラミッドとは何ですか?

あピラミッド三角錐、四角錐、五角錐、六角錐など、底辺の形状によってさまざまな種類に分類されます。頂点とは、ピラミッドの側面や側面が交わる点のことです。。ピラミッドの頂点から底部の中心までの垂直距離がピラミッドの高さまたは高度です。ピラミッドの側面の傾斜高さの頂点と底辺の間の垂直距離。

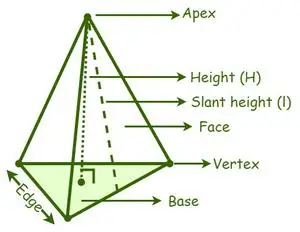
ピラミッド

三角錐の定義

三角錐 三角形を底辺としたピラミッドです。これは四面体としても知られ、3 つの三角形の面と 1 つの三角形の底面を持ち、三角形の底面はスカラー、二等辺三角形、または正三角形にすることができます。三角形はさらに、正三角錐、不規則三角錐、直角三角錐の３種類に分類される。

正三角錐: ４つの面が正三角形である三角錐を正三角錐といいます。ピラミッドは正三角形で構成されているため、すべての内角の測定値は 60°です。

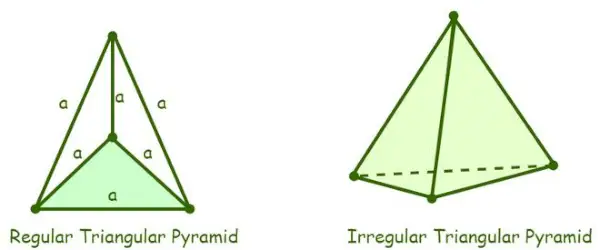
三角錐の定義

不規則な三角錐: 不規則三角錐は、底辺の辺が等しくないもの、つまり、不規則三角錐の底辺が不等辺三角形または二等辺三角形のいずれかであるものです。三角錐が不規則であると特に言及されない限り、すべての三角錐は正三角錐であると仮定されます。

直角三角錐: 直角三角錐とは、底辺が直角三角形で、その頂点が底辺の中心よりも上にあるものです。

三角錐には、三角錐の表面積と三角錐の体積という 2 つの公式があります。

三角錐の表面積
- 三角錐の側表面積
- 三角錐の総表面積
三角錐の体積

三角錐の表面積

ピラミッドの表面積には、側面の表面積と総表面積の 2 種類の表面積があります。ここで、ピラミッドの表面積は、側面または側面の面積と底面積の合計です。ピラミッドの。

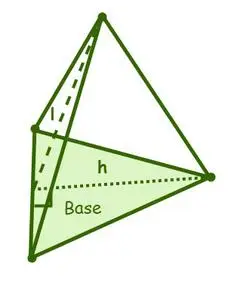
三角錐の表面積

三角錐の側表面積

三角錐の側表面積は次の式で計算されます。

三角錐の側表面積 (LSA) = 1/2 × 周長 × 傾斜高さ

三角錐の総表面積

ピラミッドの総表面積 (TSA) = ピラミッドの横表面積 + 底面の面積

したがって、TSA = 1/2 × 外周 × 傾斜高さ + 1/2 × 底辺 × 高さ

三角錐の総表面積 (TSA) = 1/2 × P × l + 1/2 bh

どこ、

P はベースの周囲長です
私はピラミッドの傾斜高さです
b 底辺の三角形の底辺です
h ピラミッドの高さです

三角錐の体積

ピラミッドの体積は、ピラミッドのすべての面の間に囲まれた空間の合計です。ピラミッドの体積は一般に文字 V で表され、その式は底面積とピラミッドの高さの積の 3 分の 1 に等しくなります。

ピラミッドの体積の公式は次のように与えられます。

三角錐の体積＝1/3×底面積×高さ

V = 1/3 × AH 立方単位

どこ、

ではピラミッドの体積です
あピラミッドの底辺の面積です
H ピラミッドの高さまたは高度です

正三角錐の体積の公式は次のようになります。

正三角錐の体積＝a ³ /6√2 立方単位

どこある isエッジの長さ

四角錐

四角錐

五角錐

六角ピラミッド

ピラミッド式の体積

ピラミッドの表面積の計算式

三角錐公式の例

例1: 底面積と高さが50cmの三角錐の体積を求める ² それぞれ12cmと12cmです。

解決：

データを考慮すると、

三角形の底辺の面積 = 100 cm²

ピラミッドの高さ = 12 cm

私達はことを知っています、

三角錐の体積（V）＝1/3×三角底面積×高さ

高さ = 1/3 × 50 × 12 = 200 cm³

したがって、与えられた三角錐の体積は 200 cm です。³。

例 2: 各辺の長さが 8 インチの場合の正三角錐の表面積の合計を求めます。

インターネットとは何ですか

解決：

データを考慮すると、

正三角錐の各辺の長さ (a) = 8 インチ

私達はことを知っています、

正三角錐の表面積の合計 = √3a²

⇒ TSA = √3 × 8²

= 64√3 = 110.851 平方インチ

したがって、正三角錐の総表面積は 110.851 平方インチです。

例3：正三角錐の辺の長さが10cmのときの体積を求めます。

解決：

データを考慮すると、

正三角錐の各辺の長さ（a）＝10cm

私達はことを知っています、

正三角錐の体積＝a³/6√2

⇒ V = (10)³/6√2

= 1000/6√2 = 117.85 cm³

したがって、正三角錐の体積は 117.85 cu です。 cm。

例 4: 三角錐の側表面積が 600 平方インチ、底面の周囲が 60 インチの場合、三角錐の傾斜高さを求めます。

解決：

データを考慮すると、

横表面積 = 600 平方インチ

ベースの周囲 = 60 インチ

私達はことを知っています、

側表面積 = 1/2 × 外周 × 傾斜高さ

600 = 1/2 × 60 × リットル

l = 600/30 = 20 インチ

したがって、指定されたピラミッドの傾斜の高さは 20 インチになります。

例 5: 底面積が 28 平方センチメートル、三角形の周囲が 18 センチメートル、ピラミッドの傾斜高さが 20 センチメートルである三角錐の総表面積を求めます。

解決：

データを考慮すると、

三角形の底面の面積 = 28 cm²

傾斜高さ (l) = 20 cm

周囲長 (P) = 18 cm

私達はことを知っています、

三角錐の総表面積 (TSA) = 1/2 × 周長 × 傾斜高さ + 底面積

⇒ TSA = 1/2 × 18 × 20 + 28

= 180 + 28 = 208 平方センチメートル

したがって、指定されたピラミッドの総表面積は 208 平方センチメートルになります。

三角錐公式の練習問題

Q1.底面積が 15 平方単位、高さが 10 単位の三角錐がある場合、ピラミッドの体積はいくらですか?

Q2.正三角形の底辺の各辺が 6 単位である正三角錐がある場合、ピラミッドの総表面積はいくらですか?

Q3.正三角形の底辺の各辺が 4 単位、高さが 5 単位である正三角錐がある場合、ピラミッドの体積と総表面積はいくらですか?

Q4.三角錐の底辺の辺の長さが 3 単位、4 単位、5 単位、ピラミッドの高さが 12 単位の場合、ピラミッドの体積はいくらですか?

Q5.直角三角形の底面に3単位と4単位の脚、5単位の斜辺をもつ三角錐の、底面から頂点までの高さが10単位のときの総表面積はいくつになりますか。 ?

三角錐公式に関するよくある質問

三角錐の定義とは何ですか?

三角錐は、三角形の底面と 3 つの三角形の面を持ち、共通の頂点を持つ幾何学的形状です。

三角錐には面と頂点はいくつありますか?

三角錐には 4 つの面と 4 つの頂点があります。 1 つの頂点はピラミッドの 3 つの面すべてに共通です。
C++で順序付けされていないマップ

ピラミッドの基本公式とは何ですか?

ピラミッドの基本的な公式は次のとおりです。

LSA = 1/2 × 外周 × 傾斜高さ

TSA = 1/2 × P × l + 1/2 bh

V = 1/3 × AH

三角錐の種類とは何ですか?

三角錐には3種類あり、

正三角錐

不規則な三角錐

直角三角錐

三角形の公式とは何ですか?

三角形の面積の公式は次のとおりです。

(面積)A = 1/2 × b × h

三角錐の公式

ピラミッドとは何ですか?

三角錐の定義