• 有限オートマトンはパターンを認識するために使用されます。
• シンボルの文字列を入力として受け取り、それに応じて状態を変更します。目的のシンボルが見つかると、遷移が発生します。
• 遷移時に、オートマトンは次の状態に移行するか、同じ状態に留まることができます。
• 有限オートマトンには 2 つの状態があります。 受け入れ状態 または 拒否状態 。入力文字列が正常に処理され、オートマトンが最終状態に達すると、受け入れられます。

FAの正式な定義

有限オートマトンは 5 つのタプル (Q、∑、δ、q0、F) の集合です。ここで、

 Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function 

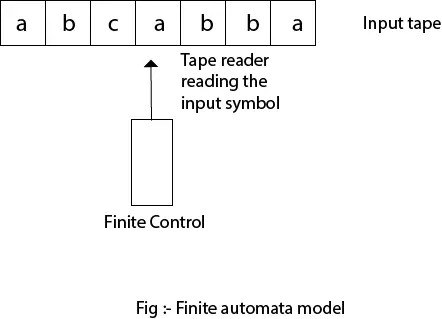
有限オートマトンモデル:

有限オートマトンは、入力テープと有限制御によって表現できます。

入力テープ: ある程度の数のセルを備えた直線状のテープです。各入力シンボルは各セルに配置されます。

有限制御: 有限制御は、入力テープから特定の入力を受け取ると次の状態を決定します。テープ リーダーはセルを左から右に 1 つずつ読み取りますが、一度に読み取られる入力シンボルは 1 つだけです。

オートマトンの種類:

有限オートマトンには 2 つのタイプがあります。

1. DFA(決定論的有限オートマトン)
2. NFA(非決定性有限オートマトン)

1.DFA

DFA は決定論的有限オートマトンを指します。決定性とは、計算の一意性を指します。 DFA では、マシンは特定の入力文字に対してのみ 1 つの状態になります。 DFA は null 移動を受け入れません。

2.NFA

NFA は非決定性有限オートマトンの略です。これは、特定の入力に対して任意の数の状態を送信するために使用されます。 null 移動を受け入れることができます。

DFA と NFA に関する重要なポイント:

1. すべての DFA は NFA ですが、NFA は DFA ではありません。
2. NFA と DFA の両方で複数の最終状態が存在する可能性があります。
3. DFA はコンパイラの字句解析で使用されます。
4. NFA は理論的な概念です。