Ford-Fulkerson アルゴリズムは、フロー ネットワークにおける最大流量問題を解決するために広く使用されているアルゴリズムです。最大フロー問題には、エッジの容量制約に従って、有向重み付けグラフ内のソース頂点からシンク頂点に送信できるフローの最大量を決定することが含まれます。
このアルゴリズムは、拡張パスを繰り返し見つけることによって機能します。これは、残差グラフ内のソースからシンクまでのパス、つまり、各エッジの容量から電流の流れを減算することによって得られるグラフです。次に、アルゴリズムは、このパスに沿ったフローを、パスに沿ったエッジの最小容量である最大可能量だけ増加させます。
問題:
すべてのエッジに容量があるフロー ネットワークを表すグラフがあるとします。また、頂点が 2 つ与えられると、 ソース '砂 シンク グラフ内の「t」について、次の制約を使用して s から t までの可能な最大流量を見つけます。
- エッジ上のフローは、エッジの指定された容量を超えません。
- s と t を除くすべての頂点について、流入するフローは流出するフローと等しくなります。
たとえば、CLRS 本にある次のグラフを考えてみましょう。
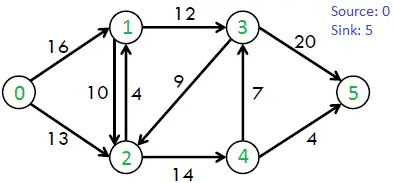
上のグラフで考えられる最大流量は 23 です。

前提条件: 最大流量問題の概要
フォード・フルカーソンアルゴリズム
以下は、Ford-Fulkerson アルゴリズムの簡単なアイデアです。
- 初期流量を 0 として開始します。
- ソースからシンクへの拡張パスが存在しますが、次のようになります。
- 幅優先検索や深さ優先検索などのパス検索アルゴリズムを使用して、拡張パスを検索します。
- 増強パスに沿って送ることができる流量を決定します。これは、パスの端に沿った最小残留容量です。
- 決定された量だけ増加経路に沿った流量を増加させます。
- 最大流量を返します。
時間計算量: 上記のアルゴリズムの時間計算量は O(max_flow * E) です。拡張パスがある間、ループを実行します。最悪の場合、反復ごとに 1 単位のフローが追加される可能性があります。したがって、時間計算量は O(max_flow * E) になります。
上記の単純なアルゴリズムを実装するにはどうすればよいでしょうか?
まず、実装を理解するために必要な残差グラフの概念を定義しましょう。
残差グラフ フロー ネットワークの追加の可能性のあるフローを示すグラフです。残差グラフにソースからシンクまでのパスがある場合、フローを追加できます。残差グラフの各エッジには、と呼ばれる値があります。 残存容量 これは、エッジの元の容量から電流を引いた値に等しくなります。残留容量は基本的にエッジの現在の容量です。
それでは、実装の詳細について説明しましょう。残差グラフの 2 つの頂点間にエッジが存在しない場合、残差容量は 0 になります。初期フローがなく、最初の残存容量は元の容量に等しいため、残差グラフを元のグラフとして初期化できます。拡張パスを見つけるには、残差グラフの BFS または DFS を実行できます。以下の実装ではBFSを使用しました。 BFS を使用すると、ソースからシンクへのパスがあるかどうかを確認できます。 BFS は、parent[] 配列も構築します。 parent[] 配列を使用して、見つかったパスをたどって、パスに沿った最小の残余容量を見つけることによって、このパスを通る可能性のあるフローを見つけます。後で、見つかったパス フローを全体のフローに追加します。
重要なことは、残差グラフの残存容量を更新する必要があるということです。パスに沿ったすべてのエッジからパス フローを減算し、逆方向のエッジに沿ってパス フローを追加します。後でフローを逆方向に送信する必要がある可能性があるため、逆方向のエッジに沿ってパス フローを追加する必要があります (たとえば、次のリンクを参照)。
以下は、Ford-Fulkerson アルゴリズムの実装です。物事を単純にするために、グラフは 2D マトリックスとして表されます。
C++
Javaの継承
// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> >'t' in residual graph. Also fills parent[] to store the> >path */> bool> bfs(>int> rGraph[V][V],>int> s,>int> t,>int> parent[])> {> >// Create a visited array and mark all vertices as not> >// visited> >bool> visited[V];> >memset>(visited, 0,>sizeof>(visited));> >// Create a queue, enqueue source vertex and mark source> >// vertex as visited> >queue<>int>>q;>> >q.push(s);> >visited[s] =>true>;> >parent[s] = -1;> >// Standard BFS Loop> >while> (!q.empty()) {> >int> u = q.front();> >q.pop();> >for> (>int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // シンク ノードへの接続が見つかった場合、 // もう BFS には意味がありません。 // その親を設定するだけでよく、 // true if (v == t) {parent[ v] = u; true を返します。 q.push(v); 親[v] = u; 訪問[v] = true; } } } // ソースから開始して BFS のシンクに到達できなかったので、 // return false return false; } // 指定されたグラフの s から t までの最大フローを返します int fordFulkerson(intgraph[V][V], int s, int t) { int u, v; // 残差グラフを作成し、その残差グラフに // 元のグラフの指定された容量を // 残差グラフの残余容量 int rGraph[V] [V]; として埋め込みます。 // rGraph[i][j] が // i から j までのエッジの残存容量を示す残差グラフ (エッジがある場合。 // rGraph[i][j] が 0 の場合、エッジは存在しない) for (u = 0; u for (v = 0; v rGraph[u][v] =graph[u][v]; intparent[V]; // この配列は BFS によって埋められ、 // パスを格納しますint max_flow = 0; // 最初はフローがありません // ソースからシンクまでのパスがある間にフローを拡張します while (bfs(rGraph, s, t,parent)) { // エッジの最小残余容量を見つけます// BFS によって埋められたパスに沿って、 // 見つかったパスを通る最大フローを見つけることもできます。 for (v = t; v != s; v =parent[v]) { u = parent[v]; path_flow = min(path_flow, rGraph[u][v]); // パスに沿ってエッジの残存容量を更新し、 // (v = t; v != s; v = parent[v]) { u =parent[v]; rGraph[v][u] += path_flow } // 全体のフローにパス フローを追加します。 // 全体的なフローを返します return max_flow; } // 上記の関数をテストするドライバー プログラム int main() { // 上記の例に示すグラフを作成しましょう int chart[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }、{ 0, 4, 0, 0, 14, 0 }、{ 0, 0, 9, 0, 0, 20 }、{ 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; コート<< 'The maximum possible flow is ' << fordFulkerson(graph, 0, 5); return 0; }> |
>
>
ジャワ
// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> >static> final> int> V =>6>;>// Number of vertices in graph> >/* Returns true if there is a path from source 's' to> >sink 't' in residual graph. Also fills parent[] to> >store the path */> >boolean> bfs(>int> rGraph[][],>int> s,>int> t,>int> parent[])> >{> >// Create a visited array and mark all vertices as> >// not visited> >boolean> visited[] =>new> boolean>[V];> >for> (>int> i =>0>; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // シンク ノードへの接続が見つかった場合、 // もはや BFS には意味がありません。 // その親を設定するだけで済みます。 // そして (v == t) {parent[ v] = u; true を返します。 キュー.add(v); 親[v] = u; 訪問[v] = true; } } } // ソースから開始して BFS のシンクに到達しませんでした。 // したがって、 return false return false; } // 指定されたグラフ内の s から t への最大フローを返します。 // int fordFulkerson(intgraph[][], int s, int t) { int u, v; // 残差グラフを作成し、残差を // 元のグラフの指定された容量でグラフに記入します // 残差グラフの残差容量として // rGraph[i][j] が示す残差グラフ // i から i までのエッジの残差容量j ( // エッジがある場合。rGraph[i][j] が 0 の場合、 // エッジはありません) int rGraph[][] = new int[V][V]; for (u = 0; u for (v = 0; v rGraph[u][v] =graph[u][v]; // この配列は BFS によって埋められ、パスを格納します。 intparent[] = new int[ V]; int max_flow = 0; // 最初はフローがありません // ソースからシンクへのパスがある間にフローを拡張します while (bfs(rGraph, s, t,parent)) { // 最小残余容量を見つけます// BFS によって埋められたパスに沿ったエッジの // または、見つかったパスを通る最大フローを見つけることもできます。 int path_flow = Integer.MAX_VALUE; for (v = t; v != s; v =parent[v ]) { u =parent[v]; path_flow = Math.min(path_flow, rGraph[u][v]) } // パスに沿ってエッジの残存容量を更新し、 // (v = t; v != s; v =parent[v]) { u =parent[u][v] -= rGraph[v][u] += path_flow; flow max_flow += path_flow; } // 全体的なフローを返します return max_flow; } // 上記の関数をテストするドライバー プログラム public static void main(String[] args) throws java.lang.Exception { // 次のグラフを作成しましょう上記の例では、 int chart[][] = new int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 、0、0、14、0 }、{ 0、0、9、0、0、20 }、{ 0、0、0、7、0、4 }、{ 0、0、0、0、0、0 } }; MaxFlow m = 新しい MaxFlow(); System.out.println('可能な最大フローは ' + m.fordFulkerson(graph, 0, 5)); } }>> |
>
>
パイソン
# Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>>0>:> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> |
>
>
C#
// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List |
>
>
JavaScript
> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) { // シンク ノードへの接続が見つかった場合、 // もはや BFS には意味がありません。 // その親を設定するだけで済みます。 // そして (v == t) {parent[ v] = u; true を返します。 キュー.プッシュ(v); 親[v] = u; 訪問[v] = true; } } } // ソースから開始して // BFS のシンクに到達しなかったので、 return false return false; } // 指定されたグラフ関数で s から t までの最大フローを返します。 fordFulkerson(graph, s, t) { let u, v; // 残差グラフを作成し、 // 残差グラフに指定された容量を入力します。 // 元のグラフに残差として // 残差グラフの容量 // rGraph[i][j] がエッジの残余容量を示す残差グラフ // / i から j まで (エッジがある場合。 // rGraph[i][j] が 0 の場合、エッジはありません。 // ありません) let rGraph = new Array(V); for(u = 0; u { rGraph[u] = new Array(V); for(v = 0; v rGraph[u][v] =graph[u][v]; } // この配列には次の値が入ります。 BFS とパスを格納します letparent = new Array(V); // 最初はフローがありません let max_flow = 0 // ソースからシンクまでのパスが存在する間にフローを拡張します while (bfs(rGraph, s, t; ,parent)) { // BFS によって満たされたパスに沿って、 // エッジの最小残存容量を見つけます。または、 // 見つかったパスを通る最大フローを見つけることもできます。 let path_flow = Number.MAX_VALUE; ; v != s; v =parent[v]) { u = path_flow = Math.min(path_flow, rGraph[u][v]); // エッジの残存容量を更新します。パスに沿ったエッジを反転します for(v = t; v != s; v =parent[v]) { u =parent[v] -= path_flow; = path_flow; } // 全体的なフローにパス フローを追加します。 max_flow += path_flow; } // 全体的なフローを返します。 return max_flow } // 上の例に示すグラフを作成しましょう let chart = [ 0 、16、13、0、0、0 ]、[ 0、0、10、12、0、0 ]、[ 0、4、0、0、14、0 ]、[ 0、0、9、0、0 , 20 ]、[ 0, 0, 0, 7, 0, 4 ]、[ 0, 0, 0, 0, 0, 0 ] ]; document.write('可能な最大フローは ' + fordFulkerson(graph, 0, 5)); // このコードは avanitrachhadiya2155 によって寄稿されました>> |
>
>出力
The maximum possible flow is 23>
時間計算量 : O(|V| * E^2) ここで、E はエッジの数、V は頂点の数です。
空間複雑度 :O(V) 、 キューを作成したとき。
上記のフォード・フルカーソン・アルゴリズムの実装は次のように呼ばれます。 エドモンズ・カープアルゴリズム 。 Edmonds-Karp のアイデアは、BFS が常に最小数のエッジを持つパスを選択するため、Ford Fulkerson の実装で BFS を使用することです。 BFS を使用すると、最悪の場合の時間計算量を O(VE2)。上記の実装では隣接行列表現が使用されていますが、BFS は O(V2) 時間、上記の実装の時間計算量は O(EV3) (参照する CLRSの本 時間計算量の証明用)
これは多くの実際の状況で発生するため、重要な問題です。例としては、指定されたトラフィック制限で転送を最大化すること、コンピュータ ネットワーク内のパケット フローを最大化することなどが挙げられます。
Dinc の Max-Flow アルゴリズム。
エクササイズ:
O(VE で実行されるように上記の実装を変更します。2) 時間。
