logo

TechCodeview

ガウス過程回帰 (GPR)

回帰および確率的分類の問題は、教師あり学習手法であるガウス プロセス (GP) を使用して解決できます。各ガウス過程は多変量の無限次元一般化として考えることができるので、 ガウス分布 、名前にガウスという用語が含まれています。この投稿では、ガウス過程回帰 (GPR) とも呼ばれる回帰のガウス過程について説明します。材料科学、化学、物理学、生物学の分野における多くの現実世界の問題は、GPR を使用して解決されています。

目次



ガウス過程回帰 (GPR)

ガウス過程回帰 (GPR) は、強力かつ柔軟なノンパラメトリック回帰手法であり、 機械学習 そして 統計 。これは、入力変数と出力の間の関係が明示的に知られていない、または複雑になる可能性がある、連続データに関係する問題を扱う場合に特に役立ちます。 GPR は、予測の確実性をモデル化できるベイジアン アプローチであり、最適化、時系列予測など、さまざまなアプリケーションにとって貴重なツールになります。 GPR は、有限数の確率変数の集合であるガウス過程の概念に基づいており、それらの有限数は結合ガウス分布を持ちます。ガウス過程は関数の分布として考えることができます。

ガウス過程回帰 (GPR) の重要な概念

ガウサンプロセス

と呼ばれるノンパラメトリックな確率モデル ガウス過程 (GP) は、回帰、分類、不確実性の定量化のために統計と機械学習で利用されます。これはランダム変数のグループを表しており、それぞれが結合ガウス分布を持ち、有限の数を持つことができます。 GP は、データ内の複雑な関係をモデル化し、関連する不確実性を伴う予測を生成するための多用途かつ効果的な手法です。

ガウス過程の特徴 :



  • ノンパラメトリックな性質 : GP は、設定された数のモデル パラメーターに依存しないため、データの複雑さに適応できます。
  • 確率的予測 : GP からの予測は確率分布として予測を提供するため、定量化できます。
  • 補間と平滑化 : GP は、ノイズのあるデータの平滑化やデータ ポイント間の補間に優れているため、ノイズのあるデータや不規則にサンプリングされたデータに役立ちます。
  • ハイパーパラメータの疎外 : 明示的なハイパーパラメータ調整の要件を排除することで、ハイパーパラメータよりも重要視されなくなり、モデルがよりシンプルになります。

平均関数

各入力点でモデル化されている関数の予測値は、次のように表されます。 平均関数 ガウス過程 (GP) で。これは、基礎となるデータ構造に関する基礎的な推定として機能します。平均関数はデフォルトでゼロに設定されることが多く、必ずしもゼロに設定される必要はありませんが、データのプロパティやドメインの専門知識に基づいて変更できます。予測の中心的な傾向に影響を与えることで、一般開業医がデータのパターンや傾向を特定するのに役立ちます。 GP は、平均関数を含めることにより、点推定だけでなく不確実性を含む確率的予測を提供します。

共分散 (カーネル) 関数

の 共分散関数 カーネル関数とも呼ばれ、ガウス過程 (GP) で入力データ ポイントが互いにどの程度類似しているかを測定します。これは GP モデルの動作を特徴付けるのに不可欠であり、以前の分布からの関数の選択に影響します。共分散関数は、ペアごとの類似性を測定して、関数値間の相関関係を確認します。カーネル関数が異なれば、異なる種類の相関関係が取得されるため、GP は、滑らかな傾向から複雑な構造に至るまで、幅広いデータ パターンに適応できます。モデルのパフォーマンスは、カーネルの選択によって大きく影響される可能性があります。

事前配布

の 事前配布 ガウス過程 (GP) では、データを観察する前に関数を理解することです。通常、それは共分散 (カーネル) 関数と平均関数によって記述されます。共分散関数はさまざまな入力点における関数値間の類似性または相関関係を表すのに対し、平均関数は以前の期待をエンコードします。これは、関数全体の分布を作成するために GP によって事前に使用されます。 GP では、データの不確実性を表す、ドメイン知識を統合する、または滑らかさを示すために事前分布を選択できます。



事後分布

ガウス過程 後日配布 データ観察後の関数に関する修正された仮定を示します。関数と以前の分布を考慮してデータの尤度をまとめます。 GP 回帰の事後分布は、観察されたデータに最もよく一致する関数にわたる分布を提供します。確率的予測と不確実性の定量化を可能にすることにより、事後分布は、事前分布に保存された事前信念とデータによって提供される情報との間のトレードオフを反映します。

ガウス過程回帰 (GPR) の数学的概念

回帰タスクでは、ガウス過程 (GP) 回帰と呼ばれるノンパラメトリックな確率的機械学習モデルが使用されます。入力変数と出力変数の間の複雑で曖昧な相互作用をモデル化する場合、これは強力なツールです。 GP 回帰では多変量ガウス分布がデータ ポイントを生成すると想定されており、目的はこの分布を推測することです。

GP 回帰モデルは次の数式で表されます。 x としましょう1、 バツ2、…..、バツnは入力データ点であり、x は実数 (-2、-1、0、1…)、(x に属します)私epsilon R)

y と仮定しましょう1、 そして2、……。、 そしてnは出力値です。ここで、y私実数 (y私epsilon R)

GP 回帰モデルは、平均関数 (mu ) と共分散関数 (k) は、入力を出力に接続する関数 f を提供します。

次に、一連のテスト位置 x* での f の分布は次の式で与えられます。

f(x^*) ∼ N(mu(x^*), k(x^*, x^*))

通常、カーネル関数は平均関数と共分散関数を定義するために使用されます。例として、頻繁に使用される二乗指数カーネルは次のように説明されます。

k(x_{i},x_{j}) = sigma^2 exp(-frac{||x_{i} – x_{j}||^2}{2l^2})

文字列に含まれる

どこ、

  • k(x_{i}, x_{j}) = カーネル関数は次のように表され、2 つの入力データ点 x 間の相関または類似性を計算します。私そして×j。
  • sigma^2 = カーネルの分散パラメータはこれです。これは、カーネル関数の規模または垂直方向の広がりを確立します。これは、データ ポイントがどの程度強く相関しているかを制御します。より高いsigma^2 より大きな分散を持つカーネル関数が得られます。
  • exp: 指数関数は、e を引数の累乗にします。
  • ||x_{i} – x_{j}||^2 : 入力データ点間の差、x私そして×j、は二乗ユークリッド距離です。特徴空間内の点間の幾何学的分離が測定されます。
  • 私2: これはカーネルの長さスケールまたは特性長を表します。これは、データ ポイントが遠くなるにつれてカーネル機能が低下する速度を制御します。 l が低いと、カーネルの劣化が早くなります。

GP 回帰モデルはベイズ推論を適用して、トレーニング データ (x, y) のセットが与えられたデータを生成した可能性が最も高い f の分布を決定します。これを行うには、データを考慮して f の事後分布を計算する必要があります。これは次のように定義されます。

p(f|x,y) =frac x,f)p(f) x)

ここで、データの周辺確率は p(y|x)、f の事前分布は p(f)、関数 f が与えられたデータの尤度は (y|x,f) です。

f の事後分布を学習した後、モデルは事後予測分布を計算して、追加のテスト ポイント x* で予測を行います。次のように定義できます。

p(f^*|x^*, y,x) = int p(f^*|x^*, f), p(f|y,x)df

どこ、

  • p(f^*|x*, y, x) = これは、トレーニング データ y と x が与えられた場合、予測された関数値 f の条件付き確率を示します。*新しい入力ポイントで x*別の言い方をすると、これは新しい入力サイト x におけるすべての潜在的な関数値にわたる確率分布です。*、観測データ y とそれらに一致する入力位置 x に条件付けされます。
  • int p(f^*|x^*, f)p(f|y,x)df = 条件付き確率を決定するために、方程式のこのセクションでは積分が使用されます。積分には、関数 f のすべての潜在的な値が含まれます。
  • p(f^*|x^*, f) = これは関数の期待値 f の条件付き確率分布です。*xで*、いくつかの中間位置に関数値 f が与えられるとします。
  • p(f|y,x) = 観測データ (y) とその入力位置 (x) を考慮すると、これは関数値 (f) の条件付き確率分布です。

不確実性を意識した意思決定やアクティブ ラーニングなどのタスクの場合、この分布は予測の不確実性の尺度を提供するため、役立ちます。

ガウス過程回帰のステップ

  • データ収集 : 回帰問題の入出力データのペアを収集します。
  • カーネル関数の選択 : 問題に合った適切な共分散関数 (カーネル) を選択します。カーネルの選択は、GPR がモデル化できる関数の形状に影響します。
  • パラメータの最適化 : データの尤度を最大化してカーネル関数のハイパーパラメータを推定します。これは、勾配降下法などの最適化手法を使用して実行できます。
  • 予測： 新しい入力が与えられた場合、トレーニングされた GPR モデルを使用して予測を行います。 GPR は、予測平均と関連する不確実性 (分散) の両方を提供します。

ガウス過程回帰 (GPR) の実装

パイソン import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()>

出力：

gpr-Geeksforgeeks

このコードでは、まずノイズを追加したサンプル データ ポイントをいくつか生成し、次に RBF カーネルを定義して、 ガウスプロセスリグレッサー それと。モデルはトレーニング データに基づいてトレーニングされ、テスト データに基づいて予測を行うために使用されます。最後に、結果はトレーニング データ、予測平均、95% 信頼区間を示すプロットで視覚化されます。

Python でのガウスプロセスの実装

Scikitラーン

パイソン import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)>

Python のガウス過程回帰 (GPR) に必要なライブラリは、このコードによってインポートされます。これらは サイピー 線形代数関数の場合、 ナムピー 数値演算の場合、および マットプロットリブ データの視覚化に。必要なパッケージとの互換性を確認するために、さらに Python のバージョンを検証し、NumPy および scikit-learn (sklearn) のバージョンとともに出力します。

カーネルの選択

パイソン np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, ' ')>

出力：

[RBF(長さ_スケール=1),
RationalQuadratic(alpha=1, length_scale=1),
ExpSineSquared(長さスケール=1、周期=10)、
DotProduct(sigma_0=1) ** 2、
母体(length_scale=1, nu=1.5)]

コードはテスト サイトの数 (n) を指定し、 ランダムシード 。選択したカーネルを表示するために、いくつかのカーネル関数のリストを生成し、そのリストを出力します。

カーネルの比較と視覚化

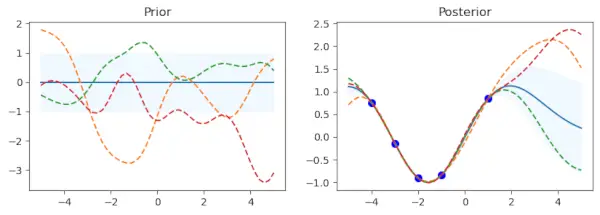
パイソン for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, ' ')>

出力：

RBF

グラフ-1-Geeksforgeeks

gp.kernel_ RBF(length_scale=1.93)
gp.log_marginal_likelihood: -3.444937833462133
-------------------------------------------------- -

有理二次方程式

グラフ-2-Geeksforgeeks

gp.kernel_ RationalQuadratic(alpha=1e+05, length_scale=1.93)
gp.log_marginal_likelihood: -3.4449718909150966
--------------------------------------------------

ExpSineSquared

グラフ-3-Geeksforgeeks

gp.kernel_ ExpSineSquared(length_scale=0.000524、周期性=2.31e+04)
gp.log_marginal_likelihood: -3.4449381454930217
--------------------------------------------------

内積

グラフ-4-Geeksforgeeks

gp.kernel_ DotProduct(sigma_0=0.998) ** 2
gp.log_marginal_likelihood: -150204291.56018084
--------------------------------------------------

母性

グラフ-5-Geeksforgeeks

gp.kernel_Matern(length_scale=1.99、nu=1.5)
gp.log_marginal_likelihood: -5.131637070524745
--------------------------------------------------

コードは、kernel_ リストにリストされているさまざまなカーネル関数をループすることから始まります。ガウス プロセス リグレッサー (gp) は、カーネルごとに特定のカーネルを使用して作成されます。ガウス過程の場合、これにより共分散構造が確立されます。以前の分布を評価するために、x_test と呼ばれるテスト入力点のセットが -5 から 5 の範囲の値で確立されます。この点のセットは列ベクトルに変換されます。

gp.predict メソッドを使用して、事前分布の平均 (mu_prior) と標準偏差 (sd_prior) が各テスト ポイントで決定されます。標準偏差値は、return_std=True オプションを使用して要求されます。 gp.サンプル_y (x_test, 3) は、前の分布から 3 つの関数サンプルを取得するために使用されます。

最初のサブプロットは、前の分布の平均を示し、標準偏差は影付きの領域で表されます。サンプルは破線で重ねられ、平均は実線で表示されます。 「Prior」と呼ばれるサブプロットがあります。トレーニング データ ポイント (x_train) とそれに付随する目標値 (y_train) の定義されたセットがあります。ガウス過程モデルは、これらの点を使用してフィッティングされます (gp.fit(x_train, y_train))。このコードでは、対応するサイン値を持つ 5 つのデータ ポイントがトレーニング データを構成します。

トレーニング データのフィッティング フェーズに続いて、このプロシージャは同じテスト ポイント (x_test) の事後分布の平均 (mu_post) と標準偏差 (sd_post) を計算します。 gp.sample_y(x_test, 3) は、事後分布から関数サンプルを生成するためにも使用されます。 2 番目のサブプロットは、サンプリングされた関数を点線で重ねて、事後分布の平均を標準偏差で陰影付けして表示します。青色でプロットされているのはトレーニング データ ポイントです。サブプロットには「事後」という名前が付いています。

現在のカーネルの前および後のプロットを確認し、モデルの動作を視覚的に理解するには、Matplotlib の plt.show() 関数を呼び出します。

このコードは、使用されている現在のカーネルを示す gp.kernel_ など、現在のカーネルに関する詳細を表示します。 gp.log_marginal_likelihood (gp.kernel_.theta)。これは、事前プロットと事後プロットの各セットの後に、現在のカーネルを使用したモデルの対数周辺尤度を示します。

ガウス過程回帰 (GPR) の利点

ガウス過程回帰 (GPR) には、さまざまなアプリケーションにおいて多くの利点があります。

  • GPR は回帰のための確率的フレームワークを提供します。つまり、点推定値を与えるだけでなく、予測の不確実性推定値も提供します。
  • 柔軟性が高く、データ内の複雑な関係をキャプチャできます。
  • GPR は、時系列予測、最適化、ベイズ最適化などのさまざまなアプリケーションに適応できます。

ガウス過程回帰 (GPR) の課題

  • GPR は、大規模なデータセットを扱う場合、共分散行列の逆行列が必要となるため、計算コストが高くなる可能性があります。
  • カーネル関数とそのハイパーパラメーターの選択は、モデルのパフォーマンスに大きな影響を与える可能性があります。

GPR アプリケーションの好例

  • 株価予測: GPR を使用すると、金融市場のボラティリティと不確実性を考慮して株価をモデル化し、予測できます。
  • コンピューター実験: GPR は、入出力関係をモデル化し、最も影響力のあるパラメーターを特定することにより、複雑なシミュレーションを最適化するのに役立ちます。
  • 異常検出: GPR は異常検出に適用でき、正常なデータ分布をキャプチャすることで時系列データ内の異常なパターンを識別します。

結論

結論として、ガウス過程回帰は、予測の不確実性を理解することが不可欠な状況において、データ分析と予測のための貴重なツールです。 GPR は、確率モデリングとカーネル機能を活用することで、正確で解釈可能な結果を​​提供できます。ただし、実際に GPR を実装する場合は、計算コストと専門家の意見の必要性を考慮することが重要です。

文字列から整数Javaに変換します