ニュートンの万有引力の法則は、重力を説明するために使用されます。重力は非接触力の一種であり、常に引力と保守的な性質を持つ力です。重力は、接触している 2 つ以上の物体が受ける引力として定義されます。重力は、重力の公式として知られるニュートンの万有引力の法則から得られる公式によって決定されます。私たちの環境は重力に囲まれています。これは、私たちの体重と、バスケットボールが投げられたときに地面に当たる前にどれだけ遠くまで跳ねるかを決定します。地球があなたに加える力は、地球の重力と同じです。あなたが地球の表面またはその近くで静止しているとき、重力はあなたの体重に等しくなります。また、自然対流による熱伝達には重力場の存在が必要です。
目次
重力の例
重力とは何ですか?
重力 または 重力 は、質量が等しいかどうかに関係なく、宇宙内の任意の 2 つの物体を引き付ける力です。ニュートンの万有引力の法則は、自分自身を含むすべての物体は互いに引き付け合うと主張しています。重力の単位はニュートンであり、N で表されます。
重力の研究は、多くの有名な科学者の貢献から多くの恩恵を受けてきました。 17 世紀初頭、イタリアの天文学者ガリレオ ガリレイは、すべての物体が地球の中心に向かって均一に加速していることを発見しました。英国の数学者アイザック ニュートンは、1687 年の画期的な研究で重力の法則を初めて発見しました。
重力は、あらゆる物体に対する影響を容易に観察できるため、基本的な力であると考えられています。したがって、重力は質量を持つすべての物体に作用します。したがって、重力は基本的な力です。物体間には接触がないため、重力は非接触になります。物体が移動する軌道の中心に焦点を結ぶため、求心性になります。体の軌道を維持する役割を担っています。回転体は、中心から離れる方向に引っ張られることになります。この引っ張りを引き起こすのは遠心力です。すべての基本的な力の中で、重力は最も弱いです。
詳しく読んでみましょう – 重力による加速度
ニュートンの万有引力の法則
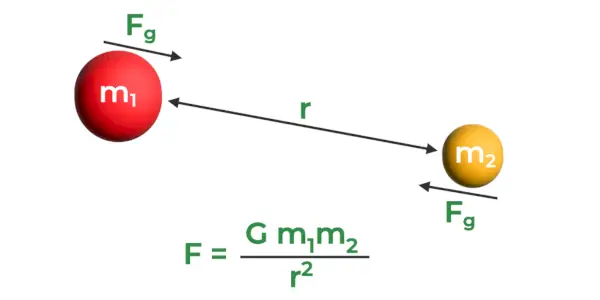
ニュートン重力公式
ニュートンの万有引力の法則 ニュートンの万有引力の法則(または万有引力の法則)は、重力のさらなる研究につながる法則であり、宇宙内の何らかの質量を持つすべての物体は常に引力で互いに引き付け合うと述べています。この引力は重力 (F) と呼ばれ、次のようになります。
- 質量の積に正比例します (m1そしてM2) 他の物体と接触している 2 つの物体、および
- 中心間の距離 (r) の 2 乗に反比例します。
上記の法則の式または関係は、以下で説明する重力の公式によって与えられます。
重力の公式
重力の法則は、2 つの質量体 (m) 間の重力 (F) を与えます。1そしてM2) 中心から離れた距離 r は次のように与えられます。
開発者モードを終了する方法F∝m 1 メートル 2
F ∝ 1/r 2
さて、上記の 2 つの関係を次のように組み合わせると、
F∝m 1 メートル 2 /r 2
F = Gm 1 メートル 2 /r 2
ここで、G は次のように知られる比例定数です。 重力定数 (= 6.67 × 10−11N・m2/kg2)。
重力の単位
- 重力のSI単位はニュートン(N)です。
- 重力の次元式は[M]1L1T-2]。
重力の性質
ここでは重力の重要な特徴をいくつか示します。
- 重力は常に引力であり、すべての基本的な力の中で最も弱いものです。
- これは、物体システムが経験する物理的な接触や接触を必要としないため、非接触力の一種です。
- 重力は長距離の力であり、媒体を必要としません。
- 地球の表面における重力の値は一定です。
こちらもお読みください: 接触部隊と非接触部隊
重力の例
重力の日常生活の例としては、次のように議論できます。
インターネットのデメリット
地球の重力
すべての物体は地球の引力、つまり重力として知られる現象の影響を受けます。私たちは重力のせいで自由に空中に浮くことはできず、地面に留まります。地球と私たち両方が惑星に加える力は等しいです。しかし、地球はその巨大な大きさのために影響を受けません。吊り下げられた物体を放すと、地球の中心方向に自然に落下します。
地球と月の間の重力
地球と月の引力により、月は地球の周りを公転します。この力を計算するために、それらの質量と 2 つの中心間の距離を重力の公式に入れます。すると、地球と月の間の重力は2×10であることが分かりました。二十N.
太陽の重力
太陽はその質量が大きいため、非常に広い範囲に重力を及ぼします。この引力により、すべての惑星は太陽の周りを楕円形に周回します。重力の公式は、太陽から地球に作用する重力を決定するために使用でき、3.5 × 10 であることがわかりました。22N.
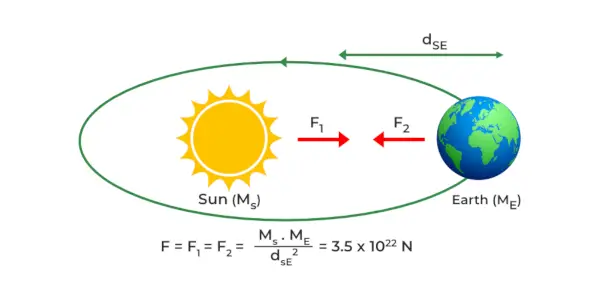
太陽の重力
重力と重力の違い
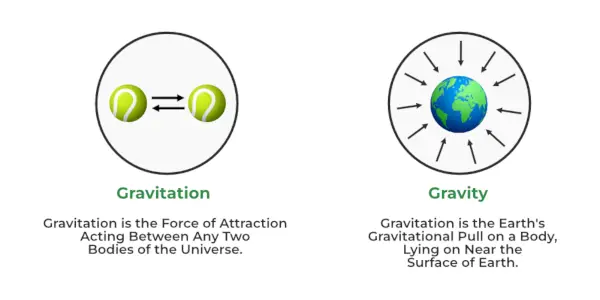
重力 vs 重力
以下の表で、重力と重力の主な違いについて詳しく説明します。
重力と重力 | |
|---|---|
重力 JavaのMVC | 重力 |
| 重力は常に引力タイプの力です。 | 重力は引力である場合もあれば、中心にある斥力タイプの力である場合もあります。 |
| これは普遍的な力ではありません。 | これは普遍的な力です。 |
| 重力は地球の中心と体の中心を結ぶ線に沿って感じられます。 | この力は質量から半径方向に沿って受けることができます。 |
続きを読む、
- 重力と重力の違い
- ケプラーの惑星運動の法則
- 重力による加速に影響を与える要因
重力の例
例 1: 2 頭のゾウの間の距離が 5 m である場合、1 頭の質量は 1000 kg、もう 1 頭の質量は 800 kg である場合の重力を求めます。
解決:
与えられた: m1= 1000kg、m2= 800 kg、r = 5 m
重力の公式は次のように与えられます: Fg=
frac{Gm_1m_2}{r^2} ここで、G = 6.67 ×10−11N・m2/kg2
式の値を代入すると、次のようになります。
Fg=
frac{6.67 ×10^{−11}N⋅ m^2/kg^2)(1000 kg)(800 kg)}{5^2} F g = 2.1 × 10 -6 N
例 2: 質量 50 kg の人間と質量 1500 kg のバスの間の距離が 10 m である場合、両者の間の引力を求めます。
解決:
与えられた: m1= 50kg、m2= 1500 kg、r = 10 m
重力の公式は次のように与えられます: Fg=
frac{Gm_1m_2}{r^2} ここで、G = 6.67 ×10−11N・m2/kg2
Javaバイト配列から文字列へ式の値を代入すると、次のようになります。
Fg=
frac{6.67 ×10^{−11}N⋅ m^2/kg^2)(50 kg)(1500 kg)}{10^2} F g = 5.0025 × 10 -8 N
例 3: ある距離にある 2 つの物体間の重力が 4 N であるとします。それらの間の距離が 2 倍になった場合の引力を求めます。
解決:
ニュートンの重力の法則は、2 つの点のような物体間の重力は、それらの質量の積に正比例し、それらの間の距離の 2 乗に反比例すると述べています。
Fg=
frac{Gm_1m_2}{r^2} 方程式は、与えられた質量に対して、r を 2r に置き換えると、力は元の力の 1/4 になることを示しています。 したがって、引力は4/4=1Nとなります。
例 4: 地球の質量は 6 × 10 24 kg。地球と太陽の距離は1.5×10 十一 メートル。両者間の重力が 3.5 × 10 の場合 22 N、太陽の質量は何ですか?
解決:
与えられた: mそれは= 6 × 1024kg、r = 1.5 × 10十一mおよびF = 3.5 × 1022N
Gimp の四角形の描画重力の公式は次のように与えられます: Fg=
frac{Gm_1m_2}{r^2} 。⇒ 3.5×1022N =
frac{6.67×10^{-11}×6×10^{24}×m_{sun}}{(1.5×10^{11})^2} ⇒ 太陽の質量 =
frac{3.5×10^{22}×2.25×10^{22}}{40.02×10^{13}} = 1.967 × 10 30 kg
重力に関するよくある質問
Q1: 重力を定義します。
重力は、質量が等しいかどうかに関係なく、宇宙内の任意の 2 つの物体を引き付ける力です。さらに、ニュートンの万有引力の法則は、あなたを含むすべてのものは宇宙の他のすべての物体を引っ張ると述べています。
Q2: 2 つの物体間の重力とは何ですか?
質量 m の 2 つの物体間の重力1そしてM2互いに離れた距離 r は、以下の式を使用して計算できます。
F = Gm 1 メートル 2 /r 2
Q3: 重力を発見したのは誰ですか?
イギリスの数学者アイザック・ニュートンは、重力の法則と重力を初めて発見しました。
Q4: 重力の 2 つの性質とは何ですか?
重力の重要な特性は次のとおりです。
- 重力は常に引力であり、すべての基本的な力の中で最も弱いものです。
- これは、物体システムが経験する物理的な接触や接触を必要としないため、非接触力の一種です。
Q5: 重力の大きさはどれくらいですか?
地球と1kgの物体との間にかかる重力の大きさは9.8Nです。
Q6: 重力の範囲はどれくらいですか?
重力の範囲は無限です。
