貪欲法は、問題を解決するために使用される分割統治と同様の戦略の 1 つです。この方法は、最適化問題を解くために使用されます。最適化問題は、最大または最小の結果を要求する問題です。いくつかの用語を通して理解しましょう。
Greedy メソッドは、最もシンプルで簡単なアプローチです。それはアルゴリズムではありませんが、テクニックです。このアプローチの主な機能は、現在入手可能な情報に基づいて決定が行われることです。現在の情報がどのようなものであっても、現在の決定が将来に与える影響を心配することなく決定が行われます。
CSV Javaから読み取る
この手法は基本的に、最適であるかどうかにかかわらず、実行可能なソリューションを決定するために使用されます。実行可能なソリューションは、指定された基準を満たすサブセットです。最適解とは、サブセット内で最良かつ最も有利な解です。実現可能の場合、複数のソリューションが指定された基準を満たす場合、それらのソリューションは実現可能とみなされますが、最適ソリューションはすべてのソリューションの中で最良のソリューションです。
Greedy法の特徴
貪欲メソッドの特徴は次のとおりです。
- 最適な方法でソリューションを構築するために、このアルゴリズムは 2 つのセットを作成します。1 つのセットには選択されたすべての項目が含まれ、もう 1 つのセットには拒否された項目が含まれます。
- Greedy アルゴリズムは、解決策が実行可能または最適であることを期待して、適切なローカル選択を行います。
貪欲なアルゴリズムのコンポーネント
貪欲アルゴリズムで使用できるコンポーネントは次のとおりです。
Javaは区切り文字で文字列を分割します
貪欲なアルゴリズムの応用
- 最短経路を見つけるために使用されます。
- これは、プリムのアルゴリズムまたはクラスカルのアルゴリズムを使用して最小スパニング ツリーを見つけるために使用されます。
- 期限付きのジョブシーケンスで使用されます。
- このアルゴリズムは、分数ナップサック問題を解くためにも使用されます。
Greedy アルゴリズムの疑似コード
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } 上記は貪欲なアルゴリズムです。最初に、解にはゼロ値が割り当てられます。配列と要素の数を貪欲アルゴリズムに渡します。 for ループ内で要素を 1 つずつ選択し、解決策が実行可能かどうかを確認します。解決策が実行可能であれば、結合を実行します。
例を通して理解しましょう。
問題「P」があるとします。以下のようなAからBへ旅行したいと考えています。
P:A→B
問題は、この旅を A から B に移動しなければならないことです。A から B に移動するにはさまざまな解決策があります。A から B に移動するには、次のようにします。 徒歩、車、自転車、電車、飛行機 など。旅には 12 時間以内に移動しなければならないという制約があります。電車か飛行機で行く場合のみ、12時間以内にこの距離をカバーできます。この問題には多くの解決策がありますが、制約を満たす解決策は 2 つだけです。
C言語の文字列配列
最低限の費用で旅費をカバーしなければならないと言えば。これは、この距離をできるだけ最小限に移動する必要があることを意味するため、この問題は最小化問題として知られています。これまでのところ、実現可能な解決策は 2 つあります。1 つは電車で、もう 1 つは飛行機です。電車での移動はコストを最小限に抑えることができるため、最適なソリューションとなります。最適なソリューションは実行可能なソリューションでもありますが、最良の結果が得られるため、そのソリューションは最小限のコストで最適なソリューションになります。最適な解決策は 1 つだけになります。
最小または最大の結果を必要とする問題は、最適化問題として知られています。貪欲法は、最適化問題を解くために使用される戦略の 1 つです。
Greedy アルゴリズムを使用するデメリット
貪欲なアルゴリズムは、より広範な問題を考慮せずに、各フェーズで利用可能な情報に基づいて意思決定を行います。したがって、貪欲な解決策ではすべての問題に対して最適な解決策が得られるわけではない可能性があります。
これは、全体的な最適値を見つけることを目的として、各段階での局所的な最適な選択に従います。例を通して理解しましょう。
以下のグラフを考えてみましょう。
Wordの透かし
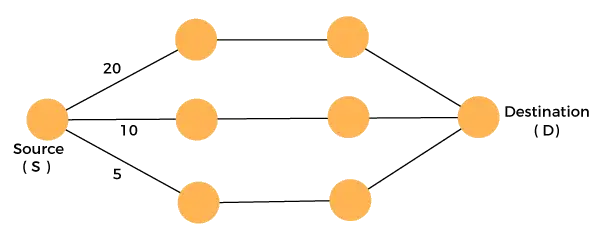
出発地から目的地まで最小限のコストで移動しなければなりません。コスト パスが 10、20、および 5 である実現可能なソリューションが 3 つあるため、5 が最小コスト パスであるため、最適なソリューションになります。これが局所最適値であり、このようにして、大域最適解を計算するために各段階で局所最適値を見つけます。
