バイナリ ツリーの高さまたは深さは、リーフ ノードからルート ノードまで、またはルート ノードからリーフ ノードまでのエッジの最大数または最大数として定義できます。ルート ノードはレベル 0 になります。つまり、ルート ノードに接続されている子ノードがない場合、特定のバイナリ ツリーの高さまたは深さはゼロであると言われます。
二分木の高さをよりよく理解するために例を見てみましょう。
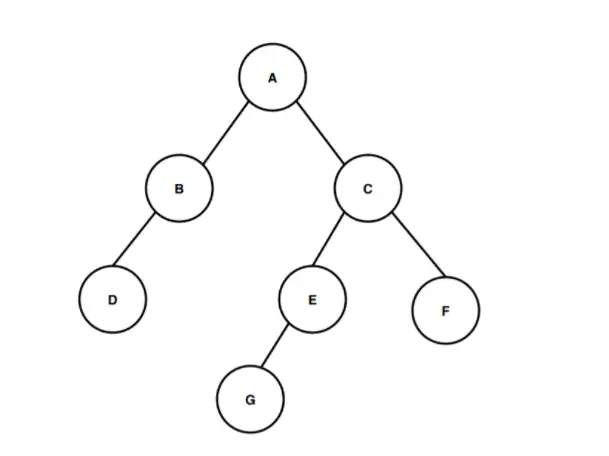
上の画像には、A という名前のルート ノードから始まるバイナリ ツリーがあります。ルート ノード A には、それぞれ左の子と右の子として 2 つの子ノード B と C があります。同様に、左側の子ノード B には D という名前の左側の子ノードが 1 つだけあり、右側の子ノード C には 2 つの子ノード E および F があり、ノード E には唯一の左側の子としてノード G があります。
数学パウJava
次に、この二分木の高さを計算してみましょう。ルート ノードから最も深いリーフ ノードまでのエッジの数を数えて、二分木の高さを計算します。この二分木に存在する最も深いノードはノード G です。したがって、この二分木の高さまたは深さを計算するには、ルート ノードと最も深いノード G の間のエッジの数を計算する必要があります。最初のエッジはノード A からノード C まで、2 番目のエッジはノード C からノード E まで、3 番目のエッジはノード E からノード G までです。したがって、ルート ノード A から最も深いノード G までトラバースするには、3 つのエッジがあります。したがって、バイナリ ツリーの高さまたは深さは 3 です。ルートから最も深いリーフ ノードに移動するためにたどったパスは A > C > E > G で、このパスは走査中に 3 つのエッジをカバーします。そのため、二分木の高さの定義では、この二分木の高さは 3 です。
二分木の高さを求める方法
ここで、二分木の高さを見つけるコードを書いてみましょう。二分木の高さを見つけるには 2 つの方法があります。 1つは、 再帰的メソッド そしてもう一つは 非再帰メソッド これは、Queue データ構造を利用してバイナリ ツリーの高さを計算します。
再帰的な方法
まず、二分木の高さを再帰的に求める方法を見てみましょう。
コード:
// Java program to create and to find the height of a binary tree by recursive way // util package is imported to use classes like Queue and LinkedList import java.util.*; // A class named Node is created representing a single node of a binary tree class Node{ // The class Node has three class variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree Node left, right; // a parameterized constructor is created to create and add data to the node at the same time. public Node(int item) { key = item; left = right = null; } } // end of node class definition // A public class named BinaryTree is created having two constructors and methods to print the binary tree level-wise. class BinaryTree{ // A static variable named root_node is created that will represent the node of the binary tree static Node root_node; // A parametrized constructor of the BinaryTree class is written having the key as a parameter BinaryTree(int key) { // here we are constructing a new node and assigning it to the root node root_node = new Node(key); } BinaryTree() { root_node = null; } // a public static function named print tree is created to print all the nodes in the tree level-wise starting from the root node public static void printTree() { int h = height(root_node); int i; for (i=1; i<=h; i++){ printcurrentlevel(root_node, i); system.out.println(); } a public static function named height is created to fund the of binary tree starting from root node deepest leaf that present in passed as parameter called recursively until returned null find int height(node root){ then will be zero if (root="=" null) return 0; else { * compute each subtree lheight="height(root.left);" rheight="height(root.right);" use larger one both sub trees calcualted and which higher used. (lheight> rheight) return(lheight+1); else return(rheight+1); } } // a Public static function named printCurrentLevel is created to print al the nodes that are present in that level // this function is called repeatedly for each level of the binary tree to print all the nodes in that particular level public static void printCurrentLevel (Node root ,int level) { if (root == null) return; if (level == 1) System.out.print(root.key + ' '); else if (level > 1) { printCurrentLevel(root.left, level-1); printCurrentLevel(root.right, level-1); } } //the main function is created to create an object of the BinaryTree class and call the printTree method to level-wise print the nodes of the binary tree and the height method to find the height of the binary tree public static void main(String[] args){ // first of all we have created an Object of the BinaryTree class that will represent the binary tree BinaryTree tree = new BinaryTree(); // now a new node with the value as 150 is added as the root node to the Binary Tree tree.root_node = new Node(150); // now a new node with the value 250 is added as a left child to the root node tree.root_node.left = new Node(250); // now a new node with the value 270 is added as a right child to the root node tree.root_node.right = new Node(270); // now a new node with the value 320 is added as a left child to the left node of the previous level node tree.root_node.left.left = new Node(320); // now a new node with the value 350 is added as a right child to the right node of the previous level node tree.root_node.left.right = new Node(350); /* 150 / 250 270 / / 320 350 null null */ System.out.println('Printing the nodes of tree level wise :'); System.out.println('Level order traversal : '); tree.printTree(); // height of the binary tree is calculated bypassing the root as parameter to the height() function. int h = tree.height(tree.root_node) System.out.println('The height of the Binary tree is : ' + h ); } } // end of the BinaryTree class </=h;> 出力: 上記のコードの出力は次のとおりです。
Printing the nodes of tree level wise: Level order traversal: (level 0) 150 (level 1) 250 270 (level 2) 320 350 The height of the Binary tree is: 2
再帰的な方法で、 身長() 関数を繰り返して二分木の高さを見つけます。バイナリ ツリーのルート ノードはパラメータとして height() 関数に渡されます。 height()関数はルートノードの両方の部分木の高さを計算し、両方の高さのうち高い方を二分木の高さとします。
非再帰的な方法
次に、二分木の高さを見つける非再帰的な方法を見てみましょう。
コード:
Javaの構造
// A C++ program to create and to find the height of a binary tree by non recursive way // iostream header file is included to use the cin and cout objects of the istream and ostream classes respectively #include #include using namespace std; // A struct named Node is created representing a single node of a binary tree struct Node { // The struct Node has three variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree struct Node* left, *right; }; // A Function named newNode is created to add a new node to the binary tree, the newNode function has one parameter of integer type named key that will represent the value that particular new node will be storing Node* newNode(int key) { Node* temp = new Node; temp->key = key; temp->left = temp->right = NULL; return (temp); } // A function named height is created to find the height of the binary tree with non recursive way // The parameter to the height function is the root node of the binary tree that will be present at level zero // In the height function the nodes of the binary tree are added into the Queue data structure and the depth variable is incremented until // the NULL node is encountered while traversing the nodes of the binary tree stored in the Queue data structure. int height(struct Node* root){ //Initialising a variable to count the //height of tree int depth = 0; queueq; //Pushing first level element along with NULL q.push(root); q.push(NULL); while(!q.empty()){ Node* temp = q.front(); q.pop(); //When NULL encountered, increment the value if(temp == NULL){ depth++; } //If NULL not encountered, keep moving if(temp != NULL){ if(temp->left){ q.push(temp->left); } if(temp->right){ q.push(temp->right); } } //If queue still have elements left, //push NULL again to the queue. else if(!q.empty()){ q.push(NULL); } } return depth; } // Start of the main function int main() { // first of all we have created an Object of the struct Node that will represent the binary tree // the value of the root node is 10 Node *root = newNode(10); // now a new node with the value 20 is added as a left child to the root node root->left = newNode(20); // now a new node with the value 30 is added as a right child to the root node root->right = newNode(30); // now a new node with the value 40 is added as a left child to the left node of the previous level node root->left->left = newNode(40); // now a new node with the value 50 is added as a right child to the left node of the previous level node root->left->right = newNode(50); /* 10 / 20 30 / / 40 50 null null */ cout<<'the height(depth) of tree is: '<<height(root); cout<<endl; } end the main function < pre> <p> <strong>Output:</strong> </p> <pre> The Height(Depth) of the tree is: 2 </pre> <p>In this approach, we have used a non recursive way to find the depth of the binary tree. To find the height of the binary tree, we have written a function named height that will require a parameter of Node type (that means the root of the binary tree whose height needs to be calculated). The root of the binary tree is present at level zero, which means the height or depth of the root is zero.</p> <p>In the non recursive approach, we use the Queue Data Structure to find the depth of the binary tree. The nodes of the binary tree for which we want to find the depth are added to the Queue data structure with the help of an enqueue operation to which the node of the binary tree is passed as a parameter to this function.</p> <p>Once all the nodes are added to the queue, the nodes added in the queue are removed by calling the dequeue function that will keep on removing one element from the queue until the null node of the binary tree is encountered. Each time a node of the binary tree from the queue is removed, the depth variable representing the depth of the binary tree is incremented by one. And in the end, the value of the depth variable will represent the final depth of the binary tree.</p> <hr></'the> このアプローチでは、非再帰的な方法を使用してバイナリ ツリーの深さを見つけました。バイナリ ツリーの高さを見つけるために、ノード タイプ (高さを計算する必要があるバイナリ ツリーのルートを意味します) のパラメータを必要とする height という名前の関数を作成しました。二分木のルートはレベル 0 に存在します。これは、ルートの高さまたは深さがゼロであることを意味します。
非再帰的アプローチでは、キュー データ構造を使用してバイナリ ツリーの深さを見つけます。深さを調べたいバイナリ ツリーのノードは、バイナリ ツリーのノードがパラメータとしてこの関数に渡されるエンキュー操作を利用して Queue データ構造に追加されます。
すべてのノードがキューに追加されると、バイナリ ツリーの null ノードが見つかるまでキューから 1 つの要素を削除し続けるデキュー関数を呼び出して、キューに追加されたノードが削除されます。バイナリ ツリーのノードがキューから削除されるたびに、バイナリ ツリーの深さを表す深さ変数が 1 ずつ増分されます。そして最終的に、深さ変数の値がバイナリ ツリーの最終的な深さを表します。
