三角形は、3 本の線の交差によって形成される 3 辺が閉じた多角形です。日常生活でもたくさん遭遇します。幾何学の基本的な形状の 1 つです。 3 つの辺、3 つの角、3 つの頂点があります。直角三角形とは、角の 1 つが常に 90°に等しい三角形です。 ピタゴラスの定理 は直角三角形について導出され、斜辺 (最長の辺) の二乗が底辺と垂線の二乗の和に等しいことを示します。
直角三角形の少なくとも 2 つの辺の長さが与えられると、直角三角形の任意の角度の値を求めることができます。このために、サイン、コサイン、タンジェント、コタンジェント、sec、cosec などのさまざまな三角関数を使用します。これらは、直角三角形の角度とその辺を関係付けるのに役立ちます。
プロパティ
- 3つの頂点の中に直角の頂点があります
- 直角の頂点の反対側を と呼びます。 斜辺 。
- 辺の長さはピタゴラスの定理に従います。
斜辺 2 = ベース 2 + 高度 2
- 斜辺は直角三角形の最も長い辺です。
- 直角以外の角度は90度未満なので鋭角となります。○
三角関数
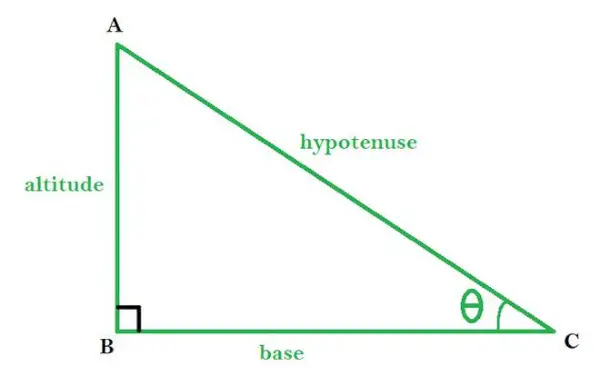
ABCは∠Bを直角とする直角三角形です
重要
- cosθ: これは、直角三角形の斜辺による底辺の比率を示します。
cosθ = 底辺 / 斜辺
- sinθ: これは、直角三角形の斜辺による高度の比率を示します。
sinθ = 高度 / 斜辺
- タンθ: 直角三角形の底辺による高度の比率です。
Tanθ = 高度 / 底辺
- コットθ: Tanθの逆数です
- 秒θ: cosθの逆数です
- cosecθ: sinθの逆数です
直角三角形の角度を見つけるには、三角形の指定された辺の比の三角関数の逆数を計算します。
例:
sinθ = x の場合、次のように書くことができます。
θ = 罪 -1 バツ。
これは、角度の正弦値が x である角度を返します。
同様に、cos が存在します。-1θ、それで-1私、ベビーベッド-1θ、秒-1θ、cosec-1私
サンプル問題
質問 1. 底辺が 10cm、斜辺が 20cm の直角三角形が与えられます。底角の値を求めます。
解決:
与えられた場合、ベース = 10cm
斜辺 = 20cm
底角の値をθとする。我々は書ける
cosθ = 底辺 / 斜辺 = 10/20 = 1/2
θ = cos-1(1/2) = 60○
したがって、底角の値は 60 です。 ○ 。
質問 2. 鋭角の一方が他方の 2 倍であるとして、直角三角形の角度の値を求めてください。
解決:
三角形の 3 つの角の合計は 180 であることがわかっているので、○。
片方の角が90度なので、○鋭角の一方が他方の 2 倍である場合、それらを θ および 2θ とみなすことができます。
したがって、次のように書くことができます
90○+θ+2θ=180○
3θ = 180○– 90○
3θ = 90○
θ = 90○/3 = 30 ○
2θ = 2 × 30○= 60 ○
つまり、角度は 30 度です ○ 、60 ○ 、 そして90 ○ 。
質問 3. はしごの根元が壁から 3m の距離にあるとして、長さ 5m のはしごの仰角の値を求めてください。
解決:
はしごは直角三角形の斜辺として機能し、底辺の距離は 3m に等しいため、次のように書くことができます。
斜辺 = 5m
ベース = 3m
仰角をθとする。したがって、次のように書くことができます
cosθ = 底辺 / 斜辺 = 3/5
θ = cos-1(3/5)
θ = 53○
したがって、仰角の値は 53 です。○。
質問 4. 標高の長さが 8 メートル、底角が 30 度である場合の斜辺の値を求めてください。 ○ 。
解決:
与えられた場合、底角は 30 に等しい○高度が 8m に等しい場合、正弦関数を適用して斜辺の長さを求めることができます。
罪30 ○ = 高度 / 斜辺
斜辺 = 高度 / sin30○
sin30の値なので○1/2 に等しいので、次のように書くことができます。
斜辺 = 高度 / (1/2) = 2 × 高度
したがって、斜辺 = 2 × 8 = 16m
したがって、斜辺の長さは 16m になります。
