AVL ツリー:
AVL ツリーは、自己バランス型の二分探索ツリー ( BST ) ここで、左と右のサブツリーの高さの差は以下を超えることはできません。 1つ すべてのノードに対して。
AVL ツリーの例:
ジャワのロゴ
すべてのノードの左右のサブツリーの高さの差が 1 以下であるため、上のツリーは AVL です。
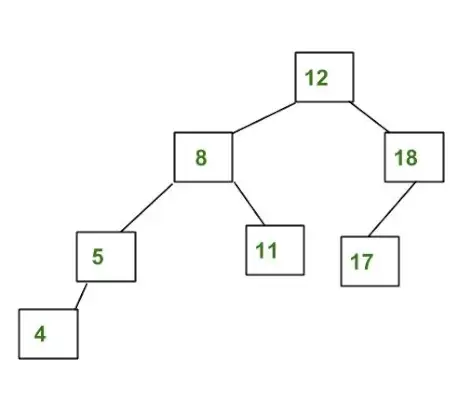
AVL ツリーではないツリーの例:

8 と 12 の左右のサブツリーの高さの差が 1 より大きいため、上記のツリーは AVL ではありません。
なぜ AVL ツリーなのか?
ほとんどの BST 操作 (検索、最大、最小、挿入、削除など) には時間がかかります。 おお) 時間どこ h BSTの高さです。これらの操作にかかるコストは、 の上) のために 歪んだ二分木 。木の高さを残しておけば O(log(n)) 挿入と削除のたびに、上限を保証できます。 O(log(n)) これらすべての操作に。 AVL ツリーの高さは常に O(log(n)) どこ n ツリー内のノードの数です。
挿入 AVL ツリー内:
指定されたツリーが挿入のたびに AVL のままであることを確認するには、標準の BST 挿入操作を拡張して再バランスを実行する必要があります。
以下は、BST プロパティに違反することなく BST のバランスをとるために実行できる 2 つの基本操作です (キー(左)
- 左回転
- 右回転
T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side) y x / Right Rotation / x T3 - - - - - - ->T1と/\<- - - - - - - / T1 T2 Left Rotation T2 T3 Keys in both of the above trees follow the following order keys(T1) < key(x) < keys(T2) < key(y) < keys(T3) So BST property is not violated anywhere.>AVL ツリー挿入の推奨練習 試してみましょう!
挿入するには次の手順に従います。
新しく挿入されたノードを次のようにします で
- 標準を実行する BST 挿入します で 。
- から始まる で 、上に移動して最初のものを見つけます アンバランスノード 。させて と 最初の不平衡ノードである、 そして になる 子供 の と それはからの道の途中にあります で に と そして バツ になる 孫 の と それはからの道の途中にあります で に と 。
- をルートとするサブツリーに対して適切な回転を実行して、ツリーのバランスを再調整します。 と。 次のように処理する必要がある 4 つのケースが考えられます。 x、y そして と 4通りのアレンジが可能です。
- 考えられる配置は次の 4 つです。
- y は z の左の子で、x は y の左の子です (左左の場合)
- y は z の左の子で、x は y の右の子です (左右の場合)
- y は z の右側の子であり、x は y の右側の子です (右右の場合)
- y は z の右の子で、x は y の左の子です (右左の場合)
上記4つの場合の操作は以下の通りです。すべての場合において、必要なのは次のことだけです。 リバランス をルートとするサブツリー と そして完全なツリーは、(適切な回転後) をルートとするサブツリーの高さとしてバランスが取れます。 と 挿入前と同じ状態になります。
1. 左左ケース
T1, T2, T3 and T4 are subtrees. z y / / y T4 Right Rotate (z) x z / - - - - - - - - ->/ / x T3 T1 T2 T3 T4 / T1 T2>
2. 左右のケース
z z x / / / y T4 Left Rotate (y) x T4 Right Rotate(z) y z / - - - - - - - - ->/ - - - - - - -> / / T1 x y T3 T1 T2 T3 T4 / / T2 T3 T1 T2>
3. 右右の場合
z y / / T1 y Left Rotate(z) z x / - - - - - - - ->/ / T2 x T1 T2 T3 T4 / T3 T4>
4. 右左ケース
z z x / / / T1 y Right Rotate (y) T1 x Left Rotate(z) z y / - - - - - - - - ->/ - - - - - - - -> / / x T4 T2 y T1 T2 T3 T4 / / T2 T3 T3 T4>
AVL ツリーへの挿入の図





アプローチ:
このアイデアは、再帰的な BST 挿入を使用することです。挿入後、ボトムアップ方式ですべての祖先へのポインターを 1 つずつ取得します。したがって、上に移動するために親ポインターは必要ありません。再帰コード自体は上に移動し、新しく挿入されたノードのすべての祖先を訪問します。
このアイデアを実装するには、以下の手順に従ってください。
- 通常のことを実行します BST挿入。
- 現在のノードは、新しく挿入されたノードの祖先の 1 つである必要があります。を更新します 身長 現在のノードの。
- バランス係数を取得する (左のサブツリーの高さ – 右のサブツリーの高さ) 現在のノードの。
- バランス係数がより大きい場合 1、 この場合、現在のノードは不均衡であり、次のいずれかの状態になります。 左 左の場合 または 左 右ケース 。であるかどうかを確認するには 左左ケース 新しく挿入されたキーと、 左サブツリールート 。
- バランス係数が以下の場合 -1 の場合、現在のノードは不均衡であり、右右の場合または右-左の場合のいずれかになります。 Right Right の場合かどうかを確認するには、新しく挿入されたキーと右側のサブツリー ルートのキーを比較します。
上記のアプローチの実装を以下に示します。
C++14
// C++ program to insert a node in AVL tree> #include> using> namespace> std;> > // An AVL tree node> class> Node> {> >public>:> >int> key;> >Node *left;> >Node *right;> >int> height;> };> > // A utility function to get the> // height of the tree> int> height(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->身長;>> }> > // A utility function to get maximum> // of two integers> int> max(>int> a,>int> b)> {> >return> (a>b)? a:b;>> }> > /* Helper function that allocates a> >new node with the given key and> >NULL left and right pointers. */> Node* newNode(>int> key)> {> >Node* node =>new> Node();> >node->キー = キー;>> >node->左 = NULL;>> >node->右 = NULL;>> >node->高さ = 1;>>// new node is initially> >// added at leaf> >return>(node);> }> > // A utility function to right> // rotate subtree rooted with y> // See the diagram given above.> Node *rightRotate(Node *y)> {> >Node *x = y->左;>> >Node *T2 = x->右;>> > >// Perform rotation> >x->右 = y;>> >y->左 = T2;>> > >// Update heights> >y->高さ = 最大(高さ(y->左),>> >height(y->右)) + 1;>> >x->高さ = 最大(高さ(x->左),>> >height(x->右)) + 1;>> > >// Return new root> >return> x;> }> > // A utility function to left> // rotate subtree rooted with x> // See the diagram given above.> Node *leftRotate(Node *x)> {> >Node *y = x->右;>> >Node *T2 = y->左;>> > >// Perform rotation> >y->左 = x;>> >x->右 = T2;>> > >// Update heights> >x->高さ = 最大(高さ(x->左),>> >height(x->右)) + 1;>> >y->高さ = 最大(高さ(y->左),>> >height(y->右)) + 1;>> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->左) - 高さ(N->右);>> }> > // Recursive function to insert a key> // in the subtree rooted with node and> // returns the new root of the subtree.> Node* insert(Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->left = insert(node->left, key);>> >else> if> (key>ノード -> キー)>> >node->right = insert(node->right, key);>> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->高さ = 1 + 最大(高さ(ノード->左),>> >height(node->右));>> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 && 左キー -> キー)>> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->右 -> キー)>> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 && キー> ノード -> 左 -> キー)>> >{> >node->left = leftRotate(ノード->左);>> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->キー)>> >node->right = rightRotate(ノード->右);>> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder> // traversal of the tree.> // The function also prints height> // of every node> void> preOrder(Node *root)> {> >if>(root != NULL)> >{> >cout ' '; preOrder(root->左); preOrder(ルート->右); } } // ドライバーコード int main() { Node *root = NULL; /* 上図に示すツリーの構築 */ root = insert(root, 10); ルート = 挿入(ルート, 20); ルート = 挿入(ルート, 30); ルート = 挿入(ルート, 40); ルート = 挿入(ルート, 50); ルート = 挿入(ルート, 25); /* 構築された AVL ツリーは 30 / 20 40 / 10 25 50 */ cout になります<< 'Preorder traversal of the ' 'constructed AVL tree is
'; preOrder(root); return 0; } // This code is contributed by // rathbhupendra> |
Java文字列をintに変換する方法
>
>
C
// C program to insert a node in AVL tree> #include> #include> > // An AVL tree node> struct> Node> {> >int> key;> >struct> Node *left;> >struct> Node *right;> >int> height;> };> > // A utility function to get the height of the tree> int> height(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->身長;>> }> > // A utility function to get maximum of two integers> int> max(>int> a,>int> b)> {> >return> (a>b)? a:b;>> }> > /* Helper function that allocates a new node with the given key and> >NULL left and right pointers. */> struct> Node* newNode(>int> key)> {> >struct> Node* node = (>struct> Node*)> >malloc>(>sizeof>(>struct> Node));> >node->キー = キー;>> >node->左 = NULL;>> >node->右 = NULL;>> >node->高さ = 1;>>// new node is initially added at leaf> >return>(node);> }> > // A utility function to right rotate subtree rooted with y> // See the diagram given above.> struct> Node *rightRotate(>struct> Node *y)> {> >struct> Node *x = y->左;>> >struct> Node *T2 = x->右;>> > >// Perform rotation> >x->右 = y;>> >y->左 = T2;>> > >// Update heights> >y->高さ = 最大(高さ(y->左),>> >height(y->右)) + 1;>> >x->高さ = 最大(高さ(x->左),>> >height(x->右)) + 1;>> > >// Return new root> >return> x;> }> > // A utility function to left rotate subtree rooted with x> // See the diagram given above.> struct> Node *leftRotate(>struct> Node *x)> {> >struct> Node *y = x->右;>> >struct> Node *T2 = y->左;>> > >// Perform rotation> >y->左 = x;>> >x->右 = T2;>> > >// Update heights> >x->高さ = 最大(高さ(x->左),>> >height(x->右)) + 1;>> >y->高さ = 最大(高さ(y->左),>> >height(y->右)) + 1;>> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->左) - 高さ(N->右);>> }> > // Recursive function to insert a key in the subtree rooted> // with node and returns the new root of the subtree.> struct> Node* insert(>struct> Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->left = insert(node->left, key);>> >else> if> (key>ノード -> キー)>> >node->right = insert(node->right, key);>> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->高さ = 1 + 最大(高さ(ノード->左),>> >height(node->右));>> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 && 左キー -> キー)>> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->右 -> キー)>> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 && キー> ノード -> 左 -> キー)>> >{> >node->left = leftRotate(ノード->左);>> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->キー)>> >node->right = rightRotate(ノード->右);>> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder traversal> // of the tree.> // The function also prints height of every node> void> preOrder(>struct> Node *root)> {> >if>(root != NULL)> >{> >printf>(>'%d '>, root->鍵);>> >preOrder(root->左);>> >preOrder(root->右);>> >}> }> > /* Driver program to test above function*/> int> main()> {> >struct> Node *root = NULL;> > >/* Constructing tree given in the above figure */> >root = insert(root, 10);> >root = insert(root, 20);> >root = insert(root, 30);> >root = insert(root, 40);> >root = insert(root, 50);> >root = insert(root, 25);> > >/* The constructed AVL Tree would be> >30> >/> >20 40> >/> >10 25 50> >*/> > >printf>(>'Preorder traversal of the constructed AVL'> >' tree is
'>);> >preOrder(root);> > >return> 0;> }> |
>
>
ジャワ
// Java program for insertion in AVL Tree> class> Node {> >int> key, height;> >Node left, right;> > >Node(>int> d) {> >key = d;> >height =>1>;> >}> }> > class> AVLTree {> > >Node root;> > >// A utility function to get the height of the tree> >int> height(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> N.height;> >}> > >// A utility function to get maximum of two integers> >int> max(>int> a,>int> b) {> >return> (a>b)? a:b;>> >}> > >// A utility function to right rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y) {> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left), height(y.right)) +>1>;> >x.height = max(height(x.left), height(x.right)) +>1>;> > >// Return new root> >return> x;> >}> > >// A utility function to left rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x) {> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left), height(x.right)) +>1>;> >y.height = max(height(y.left), height(y.right)) +>1>;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key) {> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>ノード.キー) ノード.右 = 挿入(ノード.ライト, キー); else // 重複キーは許可されません return node; /* 2. この祖先ノードの高さを更新します */ node.height = 1 + max(height(node.left), height(node.right)); /* 3. この祖先ノードのバランス係数を取得して、このノードがアンバランスになったかどうかを確認します */ int Balance = getBalance(node); // このノードがアンバランスになる場合、 // 4 つのケースがあります Left Left Case if (balance> 1 && key return rightRotate(node); // Right Right Case if (balance<-1 && key>node.right.key) return leftRotate(node); // Left Right Case if (balance> 1 && key> node.left.key) {node.left = leftRotate(node.left); rightRotate(ノード)を返します; } // 右左ケース if (バランス<-1 && key node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { System.out.print(node.key + ' '); preOrder(node.left); preOrder(node.right); } } public static void main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ System.out.println('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed by Mayank Jaiswal> |
テストの準備をする
>
>
Python3
# Python code to insert a node in AVL tree> > # Generic tree node class> class> TreeNode(>object>):> >def> __init__(>self>, val):> >self>.val>=> val> >self>.left>=> None> >self>.right>=> None> >self>.height>=> 1> > # AVL tree class which supports the> # Insert operation> class> AVL_Tree(>object>):> > ># Recursive function to insert key in> ># subtree rooted with node and returns> ># new root of subtree.> >def> insert(>self>, root, key):> > ># Step 1 - Perform normal BST> >if> not> root:> >return> TreeNode(key)> >elif> key root.left = self.insert(root.left, key) else: root.right = self.insert(root.right, key) # Step 2 - Update the height of the # ancestor node root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right)) # Step 3 - Get the balance factor balance = self.getBalance(root) # Step 4 - If the node is unbalanced, # then try out the 4 cases # Case 1 - Left Left if balance>1 とキーは self.rightRotate(root) を返します # ケース 2 - 右 バランスの場合は右<-1 and key>root.right.val: return self.leftRotate(root) # ケース 3 - バランス> 1 およびキー> の場合は左 右 root.left.val: root.left = self.leftRotate(root.left) return self.rightRotate(root ) # ケース 4 - バランスが取れている場合は右左<-1 and key root.right = self.rightRotate(root.right) return self.leftRotate(root) return root def leftRotate(self, z): y = z.right T2 = y.left # Perform rotation y.left = z z.right = T2 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def rightRotate(self, z): y = z.left T3 = y.right # Perform rotation y.right = z z.left = T3 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def getHeight(self, root): if not root: return 0 return root.height def getBalance(self, root): if not root: return 0 return self.getHeight(root.left) - self.getHeight(root.right) def preOrder(self, root): if not root: return print('{0} '.format(root.val), end='') self.preOrder(root.left) self.preOrder(root.right) # Driver program to test above function myTree = AVL_Tree() root = None root = myTree.insert(root, 10) root = myTree.insert(root, 20) root = myTree.insert(root, 30) root = myTree.insert(root, 40) root = myTree.insert(root, 50) root = myTree.insert(root, 25) '''The constructed AVL Tree would be 30 / 20 40 / 10 25 50''' # Preorder Traversal print('Preorder traversal of the', 'constructed AVL tree is') myTree.preOrder(root) print() # This code is contributed by Ajitesh Pathak> |
>
文字列Javaの文字列を置き換えます
>
C#
// C# program for insertion in AVL Tree> using> System;> > class> Node> {> >public> int> key, height;> >public> Node left, right;> > >public> Node(>int> d)> >{> >key = d;> >height = 1;> >}> }> > public> class> AVLTree> {> > >Node root;> > >// A utility function to get> >// the height of the tree> >int> height(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >int> max(>int> a,>int> b)> >{> >return> (a>b)? a:b;>> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y)> >{> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left),> >height(y.right)) + 1;> >x.height = max(height(x.left),> >height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x)> >{> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left),> >height(x.right)) + 1;> >y.height = max(height(y.left),> >height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key)> >{> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>ノード.キー) ノード.右 = 挿入(ノード.ライト, キー); else // 重複キーは許可されません return node; /* 2. この祖先ノードの高さを更新します */ node.height = 1 + max(height(node.left), height(node.right)); /* 3. この祖先ノードのバランス係数を取得して、このノードがアンバランスになったかどうかを確認します */ int Balance = getBalance(node); // このノードがアンバランスになる場合、 // 4 つのケースがあります Left Left Case if (balance> 1 && key return rightRotate(node); // Right Right Case if (balance node.right.key) return leftRotate(node) ; // 左右ケース if (balance> 1 && key> node.left.key) { node.left = leftRotate(node.left) return rightRotate(node); // 右左ケース if (balance)<-1 && key < node.right.key) { node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { Console.Write(node.key + ' '); preOrder(node.left); preOrder(node.right); } } // Driver code public static void Main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ Console.Write('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed // by PrinciRaj1992> |
>
>
JavaScript
二重リンクリスト
> > >// JavaScript program for insertion in AVL Tree> >class Node {> >constructor(d) {> >this>.key = d;> >this>.height = 1;> >this>.left =>null>;> >this>.right =>null>;> >}> >}> > >class AVLTree {> >constructor() {> >this>.root =>null>;> >}> > >// A utility function to get> >// the height of the tree> >height(N) {> >if> (N ==>null>)>return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >max(a, b) {> >return> a>b? a:b;>> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >rightRotate(y) {> >var> x = y.left;> >var> T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >leftRotate(x) {> >var> y = x.right;> >var> T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >getBalance(N) {> >if> (N ==>null>)>return> 0;> > >return> this>.height(N.left) ->this>.height(N.right);> >}> > >insert(node, key) {> >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)>return> new> Node(key);> > >if> (key node.left = this.insert(node.left, key); else if (key>node.key)node.right = this.insert(node.right, key); // 重複キーは許可されません。それ以外の場合はノードを返します。 /* 2. この祖先ノードの高さを更新します */ node.height = 1 + this.max(this.height(node.left), this.height(node.right)); /* 3. この祖先ノードのバランス係数を取得して、このノードがアンバランスになったかどうかを確認します */ var Balance = this.getBalance(node); // このノードがアンバランスになった場合、 // 4 つのケースがあります Left Left Case if (balance> 1 && key return this.rightRotate(node); // Right Right Case if (balance node.right.key) return this. leftRotate(node); // Left Right Case if (balance> 1 && key> node.left.key) { node.left = this.leftRotate(node.left); return this.rightRotate(node);左ケース if (バランス<-1 && key < node.right.key) { node.right = this.rightRotate(node.right); return this.leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node preOrder(node) { if (node != null) { document.write(node.key + ' '); this.preOrder(node.left); this.preOrder(node.right); } } } // Driver code var tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ document.write( 'Preorder traversal of the ' + 'constructed AVL tree is ' ); tree.preOrder(tree.root);> |
>
>出力
Preorder traversal of the constructed AVL tree is 30 20 10 25 40 50>
複雑さの分析
時間計算量: O(log(n))、挿入用
補助スペース: ○(1)
回転操作 (左回転と右回転) では、少数のポインターのみが変更されるため、一定の時間がかかります。高さの更新とバランス係数の取得にも一定の時間がかかります。したがって、AVL 挿入の時間計算量は BST 挿入と同じままで、O(h) (h はツリーの高さ) です。 AVL ツリーはバランスが取れているため、高さは O(Logn) になります。したがって、AVL 挿入の時間計算量は O(Logn) です。
レッドブラックツリーとの比較:
AVL ツリーや Red Black などの他の自己均衡型検索ツリーは、すべての基本操作を O(log n) 時間で完了するのに役立ちます。 AVL ツリーは、赤黒ツリーに比べてバランスが取れていますが、挿入および削除中により多くの回転が発生する可能性があります。したがって、アプリケーションで頻繁に挿入と削除が行われる場合は、Red Black ツリーを優先する必要があります。また、挿入と削除の頻度が低く、検索の操作がより頻繁である場合は、 Red Black Tree よりも AVL ツリーを優先する必要があります。
AVL ツリーの削除対象の投稿は次のとおりです。
AVL ツリー |セット 2 (削除)
