アルゴリズムの世界は美しく、高性能コンピューティングのニーズに応えるために、さまざまな戦略やツールが 24 時間開発されています。実際、アルゴリズムが自然法則からインスピレーションを得た場合、興味深い結果が観察されます。進化的アルゴリズムは、このようなアルゴリズムのクラスに属します。これらのアルゴリズムは、特定の行動やヒトゲノムの進化的特徴を模倣するように設計されています。さらに、そのようなアルゴリズム設計は人間に限定されるものではなく、特定の動物の自然な行動からもインスピレーションを得ることもできます。このような方法論を構築する基本的な目的は、従来の手段ではこれまで解決できなかった問題に対して、現実的で適切でありながら低コストの解決策を提供することです。
このような進化的アルゴリズムに基づいてさまざまな最適化手法が進化し、それによってメタヒューリスティックの領域が開かれました。 メタヒューリスティック という 2 つのギリシャ語から派生したものです。 メタ 意味 1つ上のレベル そして ヒューリスケイン 意味 見つけるには 。 Particle Swarm Optimization (PSO) や Ant Colony Optimization (ACO) などのアルゴリズムは、群れインテリジェンスとメタヒューリスティックの例です。群知能の目標は、アリ、シロアリ、ミツバチ、スズメバチなどの社会性昆虫や、鳥の群れや魚の群れなどの他の動物社会の集団行動からインスピレーションを得て、インテリジェントなマルチエージェント システムを設計することです。
背景:
アリのコロニー最適化技術は純粋に以下からインスピレーションを得ています。 採餌 アリのコロニーの行動。1990 年代にマルコ ドリゴによって初めて紹介されました。アリは真社会性の昆虫であり、個々の種としてよりも集団での生存と維持を好みます。彼らは音、触覚、フェロモンを使って互いにコミュニケーションします。 フェロモン アリによって分泌される有機化合物で、同じ種のメンバーの社会的反応を引き起こします。これらは、分泌する個体の体の外でホルモンのように作用し、受け取る個体の行動に影響を与えることができる化学物質です。ほとんどのアリは地上に生息するため、他のアリがたどる(匂いを嗅ぐ)可能性のあるフェロモンの痕跡を土壌表面に残します。
アリは集団の巣に住んでおり、ACO の基本原則は、最短経路で餌を探すために巣からのアリの動きを観察することです。最初、アリは巣の周りで食べ物を求めてランダムに動き始めます。このランダム化された探索により、巣から食料源までの複数のルートが開かれます。さて、アリは餌の質と量に基づいて、必要なフェロモン濃度を持った餌の一部を帰り道に運びます。これらのフェロモン試験に応じて、後続のアリが特定の経路を選択する確率が、食料源への指針となるでしょう。明らかに、この確率はフェロモンの濃度と蒸発速度に基づいています。また、フェロモンの蒸発速度も決定要因であるため、各経路の長さを簡単に説明できることもわかります。
Javaの歴史
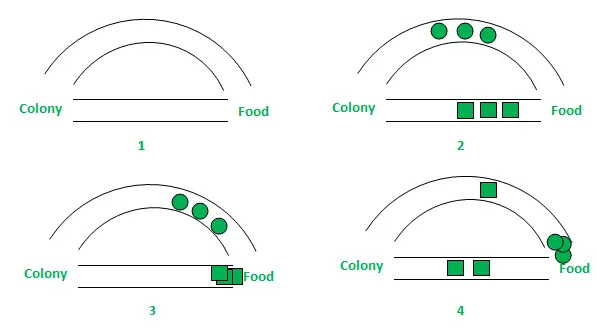
上の図では、簡単にするために、食料源とアリの巣の間の可能な経路は 2 つだけ考慮されています。段階は次のように分析できます。
- ステージ 1: すべてのアリが巣の中にいます。環境中にフェロモンは存在しません。 (アルゴリズム設計の場合、確率に干渉することなく残留フェロモン量を考慮できます) ステージ 2: アリは各パスに沿って等しい (それぞれ 0.5) 確率で探索を開始します。明らかに、曲がった経路の方が長いため、アリが食料源に到達するまでにかかる時間は他の経路よりも長くなります。ステージ 3: より短い経路を通ったアリは、より早く食料源に到達します。さて、明らかに彼らは同様の選択のジレンマに直面していますが、今回はすでに利用可能な短い経路に沿ったフェロモンの痕跡により、選択の確率が高くなります。ステージ 4: より多くのアリがより短い経路を通って戻り、その後フェロモン濃度も増加します。さらに、蒸発により、長い経路のフェロモン濃度が減少し、その後の段階でこの経路が選択される確率が減少します。したがって、コロニー全体が徐々に短い経路をより高い確率で使用するようになります。これにより、経路の最適化が実現される。
アルゴリズム設計:
アリの上記の行動に関連して、アルゴリズム設計を開発できるようになりました。簡単にするために、単一の食料源と単一のアリのコロニーを、通過可能な経路が 2 つだけあると考えます。全体のシナリオは、アリのコロニーと食料源が頂点 (またはノード) として機能する重み付きグラフを通じて実現できます。パスはエッジとして機能し、フェロモン値はエッジに関連付けられた重みとなります。
グラフを次のようにします G = (V, E) ここで、V、E はグラフのエッジと頂点です。私たちの検討による頂点は次のとおりです。 でs (ソース頂点 – アリのコロニー) および でd (目的地の頂点 – 食料源)、2 つのエッジは次のとおりです。 そして1 そして そして2 長さのある L1 そして L2 それぞれに割り当てられています。ここで、関連するフェロモン値 (フェロモンの強さを示す) は次のように仮定できます。 R1 そして R2 頂点 E の場合1そしてE2それぞれ。したがって、各アリについて、パス (E の間) の選択の開始確率は1そしてE2) は次のように表現できます。
Javaで文字列が不変である理由
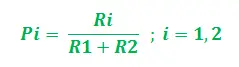
明らかに、R の場合、1>R2、E を選択する確率1の方が高く、その逆も同様です。さて、この最短経路を通って戻るときに、「E」と言います。私に対応するパスのフェロモン値が更新されます。更新は、経路の長さとフェロモンの蒸発速度に基づいて行われます。したがって、更新は次のように段階的に実現できます。
- 経路の長さに応じて –
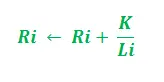
上記の更新では、i = 1、2 であり、「K」はモデルのパラメーターとして機能します。さらに、更新はパスの長さに依存します。経路が短いほど、追加されるフェロモンが高くなります。フェロモンの蒸発速度に応じて –
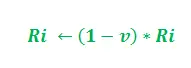
パラメータ v はフェロモンの蒸発を制御する区間 (0, 1] に属し、i = 1, 2 です。
各反復で、すべてのアリがソース頂点 V に配置されます。s(アリのコロニー)。続いてVからアリが移動sVへd次に、すべてのアリは帰還旅行を実行し、ステップ 2 に基づいて選択した経路を強化します。
ツリーマップ
疑似コード:
Procedure AntColonyOptimization: Initialize necessary parameters and pheromone trials; while not termination do : Generate ant population; Calculate fitness values associated with each ant; Find best solution through selection methods; Update pheromone trial; end while end procedure>
上記の擬似コード内のフェロモンの更新と適応度の計算は、上記の段階的な実装を通じて見つけることができます。
このようにして、ACO 最適化手法の導入が確立されました。 ACO の応用は、有名な次のようなさまざまな問題に拡張できます。 TSP(巡回セールスマン問題) 。
参考文献:
https://www.ics.uci.edu/~welling/teaching/271fall09/antcolonyopt.pdf
