二分探索木 コンピューター サイエンスでデータを整理して保存するために使用されるデータ構造です。二分探索木は二分木とそのプロパティのすべてに従います。 左 子には親ノードより小さい値が含まれており、 右 子には親ノードより大きい値が含まれています。この階層構造により、効率的な 検索中 、 挿入 、 そして 削除 ツリーに格納されたデータに対する操作。
二分探索木
結合を使用してSQLで更新する
目次
二分探索木とは何ですか?
二分探索木 (BST) の特別なタイプです 二分木 ここで、ノードの左側の子はノードの値より小さい値を持ち、右側の子はノードの値より大きい値を持ちます。このプロパティは BST プロパティと呼ばれ、ツリー内の要素の検索、挿入、削除を効率的に行うことができます。
二分探索木のプロパティ:
- ノードの左側のサブツリーには、ノードのキーよりも小さいキーを持つノードのみが含まれます。
- ノードの右側のサブツリーには、ノードのキーよりも大きいキーを持つノードのみが含まれます。
- これは、ルートの左側にあるものはすべてルートの値より小さく、ルートの右側にあるものはすべてルートの値よりも大きいことを意味します。この動作により、二分探索が非常に簡単になります。
- 左右のサブツリーもそれぞれ二分探索ツリーでなければなりません。
- 重複したノードがあってはなりません(BST には、異なる処理方法で重複した値が含まれる可能性があります)
二分探索ツリーでの重複値の処理:
- 全体を通して一貫したプロセスに従う必要があります。つまり、重複値を左側に保存するか、重複値をルートの右側に保存しますが、アプローチと一貫性を保つ必要があります。
二分探索木の基本操作:
1. BST でノードを検索します。
BST での検索とは、データ構造内の特定のノードを見つけることを意味します。二分探索木では、ノードの順序が決まっているため、ノードの検索が簡単になります。二分探索ツリーでノードを検索する手順は次のとおりです。
- まず、検索対象の要素とツリーのルート要素を比較します。
- ルートがターゲット要素と一致する場合、ノードの位置を返します。
- 一致しない場合は、項目がルート要素より小さいかどうかを確認し、ルート要素より小さい場合は、左側のサブツリーに移動します。
- ルート要素より大きい場合は、右のサブツリーに移動します。
- 一致するものが見つかるまで、上記の手順を再帰的に繰り返します。
- 要素が見つからないか、ツリー内に存在しない場合は、NULL を返します。
ここで、例を使用してバイナリ ツリーでの検索を理解しましょう。
以下に BST が与えられており、要素 6 を検索する必要があります。
コード:
以下は BST での検索の実装です。
mysqlカウントC++
// C++ function to search a given key in a given BST #include using namespace std; struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = new struct node; temp->キー = アイテム; 一時->左 = 一時->右 = NULL; 戻り温度; } // BST に指定されたキーを持つ新しいノードを挿入するユーティリティ関数 // struct node* insert(struct node* node, int key) { // ツリーが空の場合、新しいノードを返す if (node == NULL) ) newNode(key) を返します。 // それ以外の場合は、ツリーを再帰します if (key< node->キー) ノード->左 = 挿入(ノード->左, キー); else if (キー> ノード->キー) ノード->右 = insert(ノード->右, キー); // (変更されていない) ノード ポインタを返します。 return ノード; } // BST 内のキーを検索するユーティリティ関数 struct node* search(struct node* root, int key) root->key == key) return root; // キーがルートのキーより大きい if (root->key< key) return search(root->右、キー); // キーはルートのキーより小さい return search(root->left, key);>> C // C function to search a given key in a given BST #include #include struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc(sizeof(struct node)); temp->キー = アイテム; 一時->左 = 一時->右 = NULL; 戻り温度; } // BST に指定されたキーを持つ新しいノードを挿入するユーティリティ関数 // struct node* insert(struct node* node, int key) { // ツリーが空の場合、新しいノードを返す if (node == NULL) ) newNode(key) を返します。 // それ以外の場合は、ツリーを再帰します if (key< node->キー) ノード->左 = 挿入(ノード->左, キー); else if (キー> ノード->キー) ノード->右 = insert(ノード->右, キー); // (変更されていない) ノード ポインタを返します。 return ノード; } // BST 内のキーを検索するユーティリティ関数 struct node* search(struct node* root, int key)> ジャワ // Java program to search a given key in a given BST class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } } class BinarySearchTree { Node root; // Constructor BinarySearchTree() { root = null; } // A utility function to insert // a new node with given key in BST Node insert(Node node, int key) { // If the tree is empty, return a new node if (node == null) { node = new Node(key); return node; } // Otherwise, recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key>ノード.キー) ノード.右 = 挿入(ノード.ライト, キー); // (変更されていない) ノード ポインタを返します。 return ノード; } // BST でキーを検索するユーティリティ関数 Node search(Node root, int key) // 基本ケース: ルートが null またはキーがルートに存在する if (root == null>> パイソン # Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key:node.right = insert(node.right, key) # (変更されていない) ノード ポインターを返します return node # BST でキーを検索するユーティリティ関数 def search(root, key): # 基本ケース: root はroot が None または root.key == key: return root # root.key の場合、キーは root のキーより大きい場合、null またはキーがルートに存在します。< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
JavaScript // Javascript function to search a given key in a given BST class Node { constructor(key) { this.key = key; this.left = null; this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) { return new Node(key); } // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>ノード.キー) { ノード.右 = 挿入(ノード.右, キー); } // (変更されていない) ノード ポインタを返します return node; } // BST 関数でキーを検索するユーティリティ関数 search(root, key) { // 基本ケース: ルートが null またはキーがルートに存在する if (root === null || root.key === key ) { ルートを返す; } // キーがルートのキーより大きい if (root.key< key) { return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
2. BST にノードを挿入する :
新しいキーは常にリーフに挿入されます。ルートからリーフ ノードまでキーの検索を開始します。リーフ ノードが見つかると、新しいノードがリーフ ノードの子として追加されます。
コード:
以下は、二分探索ツリーへの単一ノードの挿入の実装です。
AndroidからiPhoneを探すC++
// Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->キー = アイテム; 一時->左 = 一時->右 = NULL; 戻り温度; } // BST に // 指定されたキーを持つ新しいノードを挿入する関数 struct node* insert(struct node* node, int key) { // ツリーが空の場合、新しいノードを返す if (node == NULL) return新しいノード(キー); // それ以外の場合は、ツリーを再帰します if (key< node->key) { ノード->左 = insert(ノード->左, キー); } else if (キー> ノード->キー) { ノード->右 = insert(ノード->右, キー); } // ノードポインタを返します return node; }>> C // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->キー = アイテム; 一時->左 = 一時->右 = NULL; 戻り温度; } // BST に // 指定されたキーを持つ新しいノードを挿入する関数 struct node* insert(struct node* node, int key) { // ツリーが空の場合、新しいノードを返す if (node == NULL) return新しいノード(キー); // それ以外の場合は、ツリーを再帰します if (key< node->key) { ノード->左 = insert(ノード->左, キー); } else if (キー> ノード->キー) { ノード->右 = insert(ノード->右, キー); } // ノードポインタを返します return node; }>> ジャワ class GFG { // Given Node Structure static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>ノード.キー) { ノード.右 = 挿入(ノード.右, キー); } // ノードを返します return ノード; } }>> Python3 # Given Node Structure class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key:node.right = insert(node.right, key) # ノードポインタを返す return node>>'JavaScript 時間計算量: O(N)、N は BST のノード数
補助スペース: ○(1) 3. BSTのノードを削除する :
これは、BST から特定のキーを持つノードを削除し、新しい BST を返すために使用されます。
ノードを削除するためのさまざまなシナリオ:
削除するノードはリーフノードです :
それを無効にするだけで簡単です。
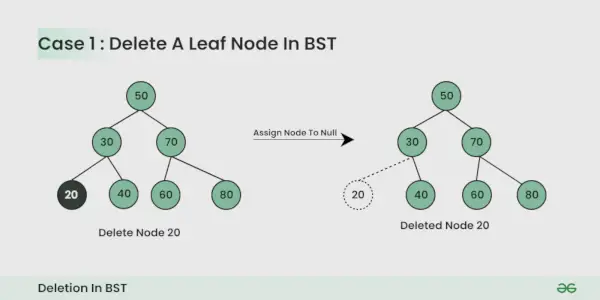
削除するノードには子が 1 つあります :
ノードを子ノードに置き換えるだけです。
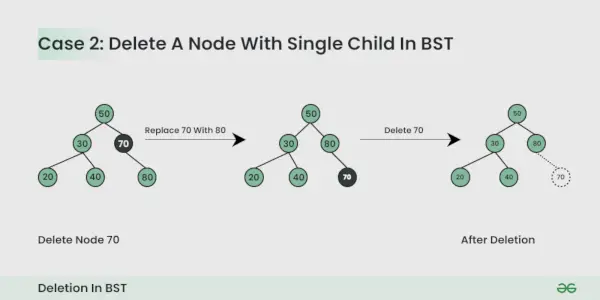
削除するノードには 2 つの子があります :
ここで私たちはしなければなりません ノードを削除すると、結果のツリーが BST のプロパティに従います。 秘訣は、ノードの順序後継者を見つけることです。インオーダーサクセサの内容をノードにコピーし、インオーダーサクセサを削除します。
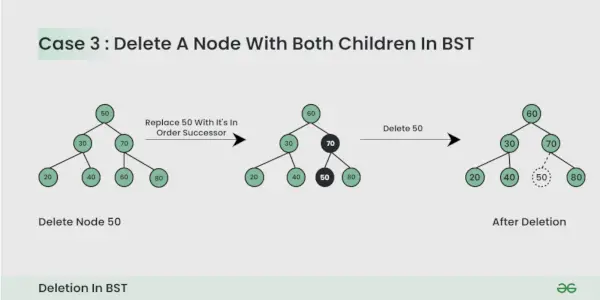
BST のノードを削除するときは、次の点に注意してください。
- 削除するノードの代替となるものを理解する必要があります。
- 既存のツリー構造への混乱を最小限に抑えたい
- 削除されたノードの左側または右側のサブツリーから置換ノードを取得できます。
- 左のサブツリーから if を取得する場合は、左のサブツリーの最大値を取得する必要があります。
- 右側のサブツリーから if を取得する場合は、右側のサブツリーの最小値を取得する必要があります。
コード:
以下は、BST での削除の実装です。
coomeetのようなウェブサイト
C++ // C++ program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->キー = アイテム; 一時->左 = 一時->右 = NULL; 戻り温度; } // BST に // 指定されたキーを持つ新しいノードを挿入する関数 struct node* insert(struct node* node, int key) { // ツリーが空の場合、新しいノードを返す if (node == NULL) return新しいノード(キー); // それ以外の場合は、ツリーを再帰します if (key< node->key) { ノード->左 = insert(ノード->左, キー); } else if (キー> ノード->キー) { ノード->右 = insert(ノード->右, キー); } // ノードポインタを返します return node; } // そのツリー内で見つかった // 最小のキー値を持つノードを返す関数 struct node* minValueNode(struct node* node) { struct node* current = node; // ループダウンして左端のリーフを見つけます while (current && current->left != NULL) current = current->left; 電流を戻します。 } // キーを削除し、 // 新しいルートを返す関数 struct node* deleteNode(struct node* root, int key) { // Base Case if (root == NULL) return root; // 削除するキーが // ルートのキーより小さい場合、 // 左側のサブツリーにあります if (key< root->key) { root->left = deleteNode(root->left, key); } // 削除するキーが // ルートのキーより大きい場合、 // 右側のサブツリーにあります。それ以外の場合、 if (key> root->key) { root->right = deleteNode(root->右、キー); } // キーが root のキーと同じ場合、 // これが削除されるノードです // else { // 子が 1 つだけあるノード // または子がない if (root->left == NULL) { struct node* temp = root->right; 無料(ルート); 戻り温度; } else if (root->right == NULL) { struct node* temp = root->left; 無料(ルート); 戻り温度; } // 2 つの子を持つノード: // 順序付けられた後継者 (// 右のサブツリーの最小のもの) を取得します。 struct node* temp = minValueNode(root->right); // 順序後継者の // コンテンツをこのノードにコピーします。 root->key = temp->key; // 後続の順序を削除 root->right = deleteNode(root->right, temp->key); ルートを返します。 }>> C // C program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->キー = アイテム; 一時->左 = 一時->右 = NULL; 戻り温度; } // BST に // 指定されたキーを持つ新しいノードを挿入する関数 struct node* insert(struct node* node, int key) { // ツリーが空の場合、新しいノードを返す if (node == NULL) return newNode(キー); // それ以外の場合は、ツリーを再帰します if (key< node->key) { ノード->左 = insert(ノード->左, キー); } else if (キー> ノード->キー) { ノード->右 = insert(ノード->右, キー); } // ノードポインタを返します return node; } // そのツリー内で見つかった // 最小のキー値を持つノードを返す関数 struct node* minValueNode(struct node* node) { struct node* current = node; // ループダウンして左端のリーフを見つけます while (current && current->left != NULL) current = current->left; 電流を戻します。 } // キーを削除し、 // 新しいルートを返す関数 struct node* deleteNode(struct node* root, int key) { // Base Case if (root == NULL) return root; // 削除するキーが // ルートのキーより小さい場合、 // 左側のサブツリーにあります if (key< root->key) { root->left = deleteNode(root->left, key); } // 削除するキーが // ルートのキーより大きい場合、 // 右側のサブツリーにあります。それ以外の場合、 if (key> root->key) { root->right = deleteNode(root->右、キー); } // キーが root のキーと同じ場合、 // これが削除されるノードです // else { // 子が 1 つだけあるノード // または子がない if (root->left == NULL) { struct node* temp = root->right; 無料(ルート); 戻り温度; } else if (root->right == NULL) { struct node* temp = root->left; 無料(ルート); 戻り温度; } // 2 つの子を持つノード: // 順序付けられた後継者 (// 右のサブツリーの最小のもの) を取得します。 struct node* temp = minValueNode(root->right); // 順序後継者の // コンテンツをこのノードにコピーします。 root->key = temp->key; // 後続の順序を削除 root->right = deleteNode(root->right, temp->key); ルートを返します。 }>> ジャワ // Java program for Delete a Node of BST class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>ノード.キー) { ノード.右 = 挿入(ノード.右, キー); } // ノードを返します return ノード; } // そのツリー内で見つかった最小のキー値を持つノードを返す関数 // static ノード minValueNode(node node) { node current = node; // ループダウンして左端のリーフを見つけます while (current != null && current.left != null) current = current.left; 電流を戻します。 } // キーを削除し、 // 新しいルートの静的ノードを返す関数 deleteNode(node root, int key) { // Base Case if (root == null) return root; // 削除するキーが // ルートのキーより小さい場合、 // 左側のサブツリーにあります if (key< root.key) { root.left = deleteNode(root.left, key); } // If the key to be deleted is // greater than the root's key, // then it lies in right subtree else if (key>root.key) { root.right = deleteNode(root.right, key); } // キーが root のキーと同じ場合、 // これが削除されるノードです // else { // 子が 1 つだけあるノード // または子が存在しない if (root.left == null) {ノード温度 = root.right; 戻り温度; } else if (root.right == null) { ノード temp = root.left; 戻り温度; } // 2 つの子を持つノード: // 順序付けられた後継者 (// 右のサブツリー内の最小のもの) ノードを取得します。 temp = minValueNode(root.right); // 順序後継者の // コンテンツをこのノードにコピーします。 root.key = temp.key; // 順序後続を削除 root.right = deleteNode(root.right, temp.key); ルートを返します。 }>> パイソン # Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = insert(root.right, key) # ノードポインタを返す return root # BST の順序トラバーサルを行う関数 def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # 最小のキー値を持つノードを返す関数 # そのツリー内で見つかったキー値 def minValueNode(node): current = node # 現在の状態でループダウンして左端のリーフを見つけますcurrent.left は None ではありません: current = current.left return current # キーを削除して # 新しいルートを返す関数 def deleteNode(root, key): # ルートが None の場合の基本ケース: return root # キーが削除されたファイルは # ルートのキーより小さい、 # キーの場合は左側のサブツリーにある< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = deleteNode(root.right, key) # キーが root のキーと同じ場合、 # これが削除されるノードです # それ以外の場合: # 子が 1 つだけあるノード # または子がありませんroot.left が None の場合: temp = root.right root = None return temp elif root.right is None: temp = root.left root = None return temp # 2 つの子を持つノード: # 順序の後継者 (最も小さい # right subtree) temp = minValueNode(root.right) # 順序後続者の # コンテンツをこのノードにコピー root.key = temp.key # 順序後続を削除 root.right = deleteNode(root.right, temp.key)ルートを返す>>'
4. トラバーサル(BSTのインオーダートラバーサル) :
二分探索ツリー (BST) の場合、Inorder traversal は非降順でノードを与えます。最初に左側の子を参照し、次にルート、次に右側の子を参照します。
以下は、二分探索ツリーの順序トラバーサルを行う方法の実装です。
C++鍵; inorder(ルート->右); } } // ドライバーコード int main() { /* 以下の BST を作成しましょう 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // BST ルートの作成 = insert(root, 50); 挿入(ルート、30); 挿入(ルート、20); 挿入(ルート、40); 挿入(ルート、70); 挿入(ルート、60); 挿入(ルート、80); // 関数呼び出し inorder(root); 0を返します。 } // このコードは shivanisinghss2110 によって提供されました>>
C // C program to implement // inorder traversal of BST #include #include // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->キー = アイテム; 一時->左 = 一時->右 = NULL; 戻り温度; } // BST に // 指定されたキーを持つ新しいノードを挿入する関数 struct node* insert(struct node* node, int key) { // ツリーが空の場合、新しいノードを返す if (node == NULL) return新しいノード(キー); // それ以外の場合は、ツリーを再帰します if (key< node->key) { ノード->左 = insert(ノード->左, キー); } else if (キー> ノード->キー) { ノード->右 = insert(ノード->右, キー); } // ノードポインタを返します return node; } // BST の順序トラバーサルを行う関数 void inorder(struct node* root) { if (root != NULL) { inorder(root->left); printf('%d ', root->key); inorder(ルート->右); } } // ドライバーコード int main() { /* 以下の BST を作成しましょう 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // BST ルートの作成 = insert(root, 50); 挿入(ルート、30); 挿入(ルート、20); 挿入(ルート、40); 挿入(ルート、70); 挿入(ルート、60); 挿入(ルート、80); // 関数呼び出し inorder(root); 0を返します。 }>> ジャワ import java.io.*; // Java program for Inorder Traversal class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>ノード.キー) { ノード.右 = 挿入(ノード.右, キー); } // ノードを返します return ノード; } // BST の順序トラバーサルを行う関数 static void inorder(node root) { if (root != null) { inorder(root.left); System.out.print(' ' + root.key); inorder(root.right); } } // ドライバーコード public static void main(String[] args) { /* 以下の BST を作成しましょう 50 / 30 70 / / 20 40 60 80 */ node root = null; // 値 50 を挿入 root = insert(root, 50); // 値 30 を挿入します insert(root, 30); // 値 20 を挿入します insert(root, 20); // 値 40 を挿入します insert(root, 40); // 値 70 を挿入します insert(root, 70); // 値 60 を挿入します insert(root, 60); // 値 80 を挿入 insert(root, 80); // BST を出力します inorder(root); } } // このコードは abhijitjadhav1998 によって寄稿されました>> Python3 # Python program to implement # inorder traversal of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to create a new BST node def newNode(item): temp = Node(item) temp.key = item temp.left = temp.right = None return temp # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return newNode(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key:node.right = insert(node.right, key) # ノードポインタを返す return node # BST の順序トラバーサルを行う関数 def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # ドライバーコード if __name__ == '__main__': # 次の BST を作成しましょう # 50 # / # 30 70 # / / # 20 40 60 80 root = なし # BST ルートの作成 = insert(root, 50) insert(root, 30) insert(root, 20) insert(root, 40) insert(root, 70) insert(root, 60) insert(root , 80) # 関数呼び出し inorder(root) #このコードは japmeet01 によって提供されています>>
出力 時間計算量: O(N)、N は BST のノード数
補助スペース: ○(1) BST のアプリケーション:
- グラフアルゴリズム: BST は、最小スパニング ツリー アルゴリズムなどのグラフ アルゴリズムを実装するために使用できます。
- 優先キュー: BST を使用すると、優先度キューを実装できます。優先度が最も高い要素がツリーのルートにあり、優先度の低い要素はサブツリーに格納されます。
- 自己平衡二分探索木: BST は、AVL ツリーや赤黒ツリーなどの自己バランス型データ構造として使用できます。
- データの保存と取得: BST を使用すると、データベースなどにデータを迅速に保存および取得でき、特定のレコードの検索を対数時間で実行できます。
利点:
- 高速検索: BST 内の特定の値の検索の平均時間計算量は O(log n) です。ここで、n はツリー内のノードの数です。これは、最悪の場合の時間計算量が O(n) である配列またはリンク リスト内の要素の検索よりもはるかに高速です。
- 順序通りの走査: BST は、左のサブツリー、ルート、右のサブツリーを順にたどることができます。これを使用してデータセットを並べ替えることができます。
- スペース効率: BST は、配列やリンク リストとは異なり、冗長な情報を格納しないため、スペース効率が高くなります。
短所:
- 歪んだ木: ツリーが歪むと、検索、挿入、および削除操作の時間計算量が O(log n) ではなく O(n) になり、ツリーの効率が低下する可能性があります。
- 追加の所要時間: 自己バランス ツリーでは、挿入および削除操作中にバランスを維持するために追加の時間が必要です。
- 効率: BST は、重複が多いデータセットではスペースを無駄にするため効率的ではありません。
FAQ(よくある質問)二分探索木上:
1. 二分探索木とは何ですか?
二分探索木 (BST) は、 左側のサブツリーのすべてのノードがルートより小さく、右側のサブツリーのすべてのノードがルートより大きい値を持つバイナリ ツリー 。二分探索木のプロパティは再帰的です。任意のノードをルートとみなした場合、これらのプロパティは true のままになります。
2. 二分探索木演算とは何ですか?
二分探索木には主に 3 つの操作があります。 1. 挿入、2. 削除、3. 検索。 その特性により、二分探索ツリー内の任意の要素を効率的に検索できます。
3. 二分探索木と AVL 木とは何ですか?
二分探索木 : 二分探索木 (BST) は、左側のサブツリーのすべてのノードがルートより小さく、右側のサブツリーのすべてのノードがルートより大きい値を持つ二分木です。
AVL ツリー : 自己バランスをとり、自動的に回転する二分探索ツリー (BST) は、AVL ツリーとして知られています。
4. 二分探索ツリーの用途は何ですか?
二分探索ツリーを使用して、次のような抽象データ型を実装できます。 動的セット、ルックアップ テーブル、優先キュー、 で使用されています ソートアルゴリズム ツリーソートなど。
5. 二分探索木と二分木の違いは何ですか?
二分探索木は、要素を配置するために何らかの順序に従っている木ですが、二分木はいかなる順序にも従いません。
ラム俳優
関連記事:
- BSTの適用
- 二分探索木の用途、メリット、デメリット
- 二分探索木 (BST) への挿入
- 二分探索木 (BST) での検索
- 二分探索木 (BST) での削除



