目で見たり触れたりできるあらゆる物体の長さ、幅、高さの 3 つの寸法を測定できます。私たちが住んでいる家には特定の寸法があります。あなたが見ている長方形の表示画面/モニターには、幅と長さの幅があります。あらゆる三次元幾何学的構造について、表面積と体積が測定されます。
物体の表面が覆う面積は、特定の物体の表面積です。一方、オブジェクト内で利用可能な空間の量は体積です。
目次
表面積
表面積と体積は、あらゆる 3 次元 (3D) 幾何学的形状について計算できます。任意の領域の表面とは、オブジェクトの表面が占める領域です。体積とは、オブジェクト内で利用可能なスペースの量です。半球、球、立方体、直方体、円柱など、さまざまな種類の形状があります。すべての 3 次元形状には面積と体積があります。ただし、正方形、長方形、三角形、円などの 2 次元の形状です。
ここでは 2 次元で、面積しか測定できません。三次元物体の外表面が占める面積を表面積といいます。平方単位で測定されます。
エリアには次の 2 つのタイプがあります。
- 総表面積
- 曲面面積・側面面積
総表面積
底面と湾曲部分を含む面積が全表面積に相当します。物体の表面で囲まれた面積のことです。フォームの底面と表面が湾曲している場合、2 つの領域の合計が総面積になります。総表面積は、基部と湾曲部分を含むオブジェクトによってカバーされる総面積として定義できます。オブジェクトに底面と湾曲した領域の両方がある場合、総表面積は底面と湾曲した領域の合計に等しくなります。
- 総表面積は、物体が占める総面積です。
- たとえば、直方体を例に挙げます。直方体には 6 つの面、12 の辺、8 つの頂点があります。
総表面積 = ベース面積 + 曲面面積
抽象クラスJava
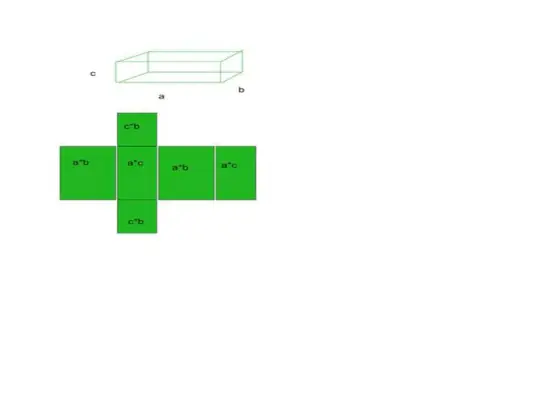
- これらの合計 6 つの領域の合計が、特定の形状の総表面積になります。
例:
以下に、長さ = 8 cm、幅 = 4 cm、高さ = 6 cm の寸法を持つ直方体を示します。直方体の TSA を求めます。
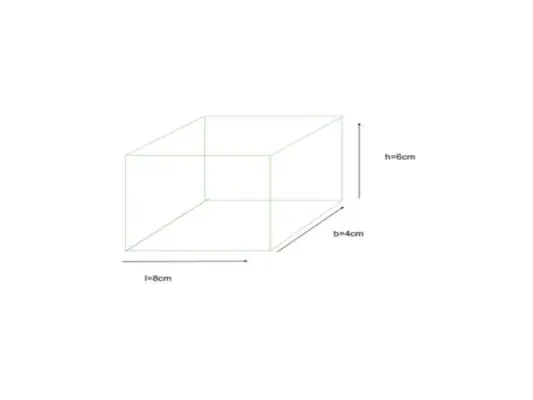
l = 8cm、b = 4cm、h = 6cm とすると
TSA = 2((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2(104)
= 208
直方体のTSAは208cmです。
曲面面積・側面面積
曲面面積は、その中心を除く、形状の曲面部分のみの面積に相当します。円錐などの形状の場合は、側面の表面積と呼ばれることがよくあります。側面面積は、物体の曲面領域のみを含む面積、または物体の底面積を除いた物体の側面面積として定義できます。側面面積は曲面面積としても知られています。
ほとんどの形状またはオブジェクトは曲面領域を指し、形状またはオブジェクトのような円柱は側面領域を指します。簡単に言うと、私たちの目に見える領域を側面領域と呼びます。たとえば、次の図に示すような円柱について考えてみましょう。
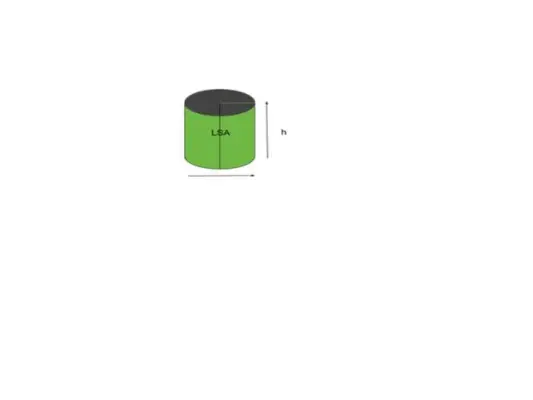
音量
体積とは、特定の 3D オブジェクト内の空間の量です。物体または物質が占める空間の総量は、体積と呼ばれます。立方単位で測定されます。
表面積と体積の公式
与えられた表には、さまざまな形状の総表面積、曲面面積/側面積、および体積が含まれています。
| 形状の名前 | 曲面領域 | 総表面積 | 音量 |
|---|---|---|---|
| 直方体 | 2時間(l + b) | 2(ポンド+bh+hl) | l * b * h |
| キューブ | 4a2 | 6a2 | ある3 |
| シリンダー | 2πrh | 2π(r + h) | πr2h |
| 球 | 4πr2 文字列とJava | 4πr2 | 4/3πr3 |
| 円錐 | πrl | πr(r + l) | 1/3πr2h |
| 半球 | 2名様2 | 3πr2 | 2/3πr3 |
続きを読む:
- ピラミッドの表面積
- シリンダーの表面積
- 半球の表面積
- 球の表面積
- 直方体の表面積
表面積と体積の例
例 1: 体積 512 cm の立方体 2 つ 3 端から端まで結合されています。得られた直方体の表面積を求めますか?
解決:
考えると、
各立方体の体積 (V) = 512 cm3
これで、3= 512cm3
∴立方体の一辺、つまり a = 8 cm
これで、直方体の幅と長さはそれぞれ 8 cm、高さは 16 cm になります。
したがって、直方体の表面積 (TSA) = 2(lb + bh + lh)
ここで、値を入力すると、次のようになります。
= 2(8×16+8×8+16×8)cm 2
= (2 × 320) = 640 cm 2
したがって、直方体の TSA = 640 cm 2
例 2: 直径 14 cm、長さ 2 cm の円筒形のキャンドルがあります。 これを溶かして7cm×11cm×1cmの直方体のキャンドルを作ります。直方体キャンドルは何個入手できますか?
解決:
円筒形キャンドルの寸法:
円筒形キャンドルの半径 = 14/2 cm = 7 cm
高さ/厚さ=2cm
1本の円筒ローソクの体積 = πr2h = π x 7 x 7 x (2) cm3= 308cm3。
直方体の体積 キャンドル = 7 x 11 x 1 = 77 cm3
したがって、直方体ろうそくの数 = 直方体ろうそくの体積 / 1 本の円筒形ろうそくの体積 = 308/77 = 4
したがって、4つの直方体のキャンドルが得られます。
例 3: 女性は、身に着けているバングルの半径と同じ半径を持つ粘土で球形のおもちゃのボールを作りたいと考えています。バングルの形状が円形であることを考慮すると、彼女はバングルの面積が球の体積と等しいことも望んでいます。彼女が着けているバングルの半径を調べてください?
解決:
r をバングルと球の半径とします。
球の体積はバングルの面積に等しいと仮定しています。
したがって、
πr2= 4/3 πr3
⇒ r = 3/4
したがって、バングルの半径は 3/4 単位です。
例 4: 直円錐の傾斜高さが 25 cm、その高さが 24 cm であるとします。円錐の曲面面積を求めますか?
解決:
円錐の曲面面積の公式は πrl です。ここで、r は円錐の半径、l は円錐の傾斜の高さです。
ここでの円錐は右円錐です。
したがって、円錐の半径は次のようになります。
r= sqrt{l^2 – h^2}
=>r = sqrt{25^2 – 24^2}
パーセイントJava=> r = 7 cm。
曲面の計算は次のようになります。
必要な面積 = (22/7) * 7 * 25 = 550 cm2
したがって、円錐の曲面面積は 550 cm です。 2 。
例 5: 底面半径 6 インチ、高さ 14 インチの円柱の側面面積を求めます。
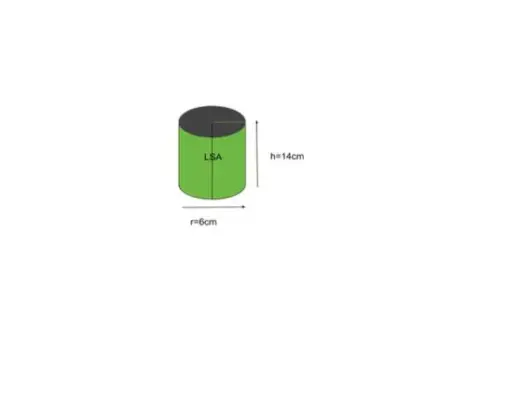
解決:
半径 r = 6、高さ h = 14 とすると、
LSA = 2∏rh
= 2 * ∏ * 6 * 14
= 168∏
= 527,787
= 528。
指定されたシリンダーの LSA は 528cm です 。
表面積と体積に関する練習問題
様々な 表面積と体積に関する練習問題 式は次のとおりです。
Q1.一辺の長さが5センチメートルの立方体の表面積を求めます。
Q2.半径 3 メートルの球の体積を計算します。
Q3.半径 4 センチメートル、高さ 8 センチメートルの円柱の総表面積を求めます。
Q4.半径 6 インチ、高さ 10 インチの円錐の体積を求めます。
Q5.長さ7メートル、幅4メートル、高さ6メートルの直方体の表面積を計算します。
表面積と体積の式に関する FAQ
表面積と体積の公式は何ですか?
上記の記事には、さまざまな表面積と体積の公式が追加されています。
表面積体積クラス 10 の計算式は何ですか?
表面積と体積クラス 10 の式には次のものが含まれます。
| 形状の名前 | 曲面領域 | 総表面積 | 音量 |
|---|---|---|---|
| 直方体 NFA を DFA に変換します | 2時間(l + b) | 2(ポンド+bh+hl) | l × b × h |
| キューブ | 4a2 | 6a2 | ある3 |
| シリンダー | 2πrh | 2π(r + h) | πr2h |
| 球 | 4πr2 | 4πr2 | 4/3πr3 |
| 円錐 | πrl | πr(r + l) | 1/3πr2h |
| 半球 | 2名様2 | 3πr2 | 2/3πr3 |
直方体の表面積と体積の公式は何ですか?
- 直方体の表面積 = 2(lb + bh + hl)
- 立方体の体積 = l × b × h
表面積と体積とは何ですか?
表面積は固体のすべての表面の面積であり、その体積はスロイドが占める空間です。
