あ 最小ヒープ のタイプとして定義されます ヒープ データ構造は、データの並べ替え、検索、整理などのさまざまな目的でコンピューター サイエンスで一般的に使用されるバイナリ ツリーの一種です。
Min-Heap の概要 – データ構造とアルゴリズムのチュートリアル
Min-Heap の目的と使用例:
- 優先キューの実装: ヒープ データ構造の主な用途の 1 つは、優先キューを実装することです。
- ダイクストラのアルゴリズム : ダイクストラのアルゴリズムは、グラフ内の 2 つのノード間の最短経路を見つける最短経路アルゴリズムです。最小ヒープを使用すると、ソース ノードからの距離が最小の未訪問のノードを追跡できます。
- 並べ替え: 最小ヒープは、要素のコレクションを昇順で効率的に並べ替えるための並べ替えアルゴリズムとして使用できます。
- 検出結果の中央値: 最小ヒープを使用すると、数値ストリームの中央値を効率的に見つけることができます。数値の大きい半分を保存するために 1 つの最小ヒープを使用し、小さい半分を保存するために 1 つの最大ヒープを使用できます。中央値は最小ヒープのルートになります。
さまざまな言語での最小ヒープ データ構造:
1. C++ の最小ヒープ
最小ヒープは、次を使用して実装できます。 優先キュー 標準テンプレート ライブラリ (STL) からのコンテナー。の 優先キュー コンテナは、各要素に優先順位が関連付けられたキューのようなデータ構造に要素を格納する方法を提供するコンテナ アダプタの一種です。
構文 :
C++ priority_queue < int, vector 、より大きい >分H;>>
2. Javaの最小ヒープ
Java では、最小ヒープは次を使用して実装できます。 優先キュー からのクラス java.util パッケージ 。 PriorityQueue クラスは、各要素に関連付けられた優先順位を持つキューのようなデータ構造に要素を格納する方法を提供する優先キューです。
構文 :
LinuxでJavaのバージョンを確認するジャワ
PriorityQueue minHeap = 新しい PriorityQueue ();>>
3. Python の最小ヒープ
Python では、最小ヒープは次を使用して実装できます。 ヒープク ヒープを実装するための機能を提供するモジュール。具体的には、 ヒープク モジュールは、ヒープ データ構造を作成および操作する方法を提供します。
構文:
パイソン heap = [] heapify(heap)>
4. C# の最小ヒープ
C# では、最小ヒープは、 System.Collections.Generic 名前空間 。 PriorityQueue クラスは、各要素に関連付けられた優先順位を持つキューのようなデータ構造に要素を格納する方法を提供する優先キューです。
構文:
C# var minHeap = new PriorityQueue ();>>
5. JavaScript の最小ヒープ
最小ヒープは、すべてのノードがその子以下の値を持つバイナリ ツリーです。 JavaScript では、配列を使用して最小ヒープを実装できます。最初の要素はルート ノードを表し、インデックスにあるノードの子を表します。 私 インデックスにあります 2i+1 そして 2i+2。
構文:
JavaScript const minHeap = new MinHeap();>
最小ヒープと最大ヒープの違い:
|
| 最小ヒープ | 最大ヒープ |
|---|---|---|
| 1. | Min-Heap では、ルート ノードに存在するキーは、そのすべての子に存在するキー以下である必要があります。 | Max-Heap では、ルート ノードに存在するキーは、そのすべての子に存在するキー以上である必要があります。 |
| 2. | Min-Heap では、最小のキー要素がルートに存在します。 | Max-Heap では、最大のキー要素がルートに存在します。 |
| 3. | 最小ヒープでは昇順の優先順位が使用されます。 | Max-Heap では降順の優先順位が使用されます。 |
| 4. | Min-Heap の構築では、最小の要素が優先されます。 | Max-Heap の構築では、最大の要素が優先されます。 |
| 5. | Min-Heap では、最小の要素が最初にヒープからポップされます。 | Max-Heap では、最大の要素が最初にヒープからポップされます。 |
最小ヒープ データ構造の内部実装:
あ 最小ヒープは通常、配列として表されます 。
- ルート要素は次の場所になります。 到着[0] 。
- 任意の i 番目のノードの場合 到着[i] :
- 配列[(i -1) / 2] 親ノードを返します。
- Arr[(2 * i) + 1] 左の子ノードを返します。
- Arr[(2 * i) + 2] 右の子ノードを返します。
Min-Heap の内部実装には、次の 3 つの主要な手順が必要です。
- 挿入 : 最小ヒープに要素を挿入するには、まず要素を配列の末尾に追加し、次に要素が正しい位置になるまで要素とその親を繰り返し交換することでヒープ プロパティを調整します。
- 削除 : 最小ヒープから最小要素を削除するには、まずルート ノードを配列内の最後の要素と交換し、最後の要素を削除してから、要素が最小の子と要素を繰り返し交換してヒープ プロパティを調整します。正しい位置。
- ヒーピファイ : heapify 操作を使用して、ソートされていない配列から最小ヒープを作成できます。
最小ヒープ データ構造の操作とその実装:
ヒープ データ構造に対して実行できる一般的な操作をいくつか示します。
1. 最小ヒープ データ構造への挿入 :
要素は、削除に関して上で説明したのと同様のアプローチに従ってヒープに挿入できます。アイデアは次のとおりです。
- 最小ヒープへの挿入操作には、次の手順が含まれます。
- 新しい要素をヒープの末尾、つまりツリーの最終レベルの次に使用可能な位置に追加します。
- 新しい要素をその親と比較します。親が新しい要素より大きい場合は、それらを交換します。
- 親が新しい要素以下になるまで、または新しい要素がツリーのルートに到達するまで、手順 2 を繰り返します。
- 新しい要素は最小ヒープ内の正しい位置に配置され、ヒープ プロパティは満たされています。
図:
ヒープが次のような最小ヒープであると仮定します。
最小ヒープへの挿入
Min-Heap での挿入操作の実装:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // 新しい要素をヒープの最後に追加します heap.push_back(value); // 最後の要素のインデックスを取得 int index = heap.size() - 1; // 新しい要素をその親と比較し、 // 必要に応じて交換します while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // ツリーを現在の要素の親に移動します。 //index = (index - 1) / 2; } } // insert_min_heap をテストするメイン関数 function int main() { Vector ヒープ; int 値[] = { 10, 7, 11, 5, 4, 13 }; int n = sizeof(values) / sizeof(values[0]); for (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); cout << 'Inserted ' << values[i] << ' into the min-heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; } return 0; }>
ジャワ import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(int[] heap, int size, int value) { // Add the new element to the end of the heap heap[size] = value; // Get the index of the last element int index = size; // Compare the new element with its parent and swap // if necessary while (index>0 && ヒープ[(インデックス - 1) / 2]> ヒープ[インデックス]) { swap(ヒープ, インデックス, (インデックス - 1) / 2); // ツリーを現在の要素の親に移動します。 //index = (index - 1) / 2; } } // 配列内の 2 つの要素を交換する関数 public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = 温度; } // insertMinHeap 関数をテストするメイン関数 public static void main(String[] args) { int[] heap = new int[6]; int[] 値 = { 10, 7, 11, 5, 4, 13 }; 整数サイズ = 0; for (int i = 0; i< values.length; i++) { insertMinHeap(heap, size, values[i]); size++; System.out.print('Inserted ' + values[i] + ' into the min-heap: '); for (int j = 0; j < size; j++) { System.out.print(heap[j] + ' '); } System.out.println(); } } }> Python3 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 および heap[(index - 1) // 2]> heap[index]: heap[index], heap[(index - 1) // 2] = heap[(index - 1) // 2], heap[ Index] # ツリーを現在の要素の親に移動します。index = (index - 1) // 2 heap = []values = [10, 7, 11, 5, 4, 13] for value invalues: insert_min_heap( heap, value) print(f'{value} を最小ヒープに挿入しました: {heap}')> C# using System; using System.Collections.Generic; public class Program { // Function to insert a new element into the min-heap static void InsertMinHeap(List heap, int value) { // 新しい要素をヒープの末尾に追加します heap.Add(value); // 最後の要素のインデックスを取得 int index = heap.Count - 1; // 新しい要素をその親と比較し、 // 必要に応じて交換します while (index> 0 && heap[(index - 1) / 2]> heap[index]) { int temp = heap[index]; ヒープ[インデックス] = ヒープ[(インデックス - 1) / 2]; ヒープ[(インデックス - 1) / 2] = 温度; // ツリーを現在の要素の親に移動します。 //index = (index - 1) / 2; } } // InsertMinHeap 関数をテストするメイン関数 public static void Main() { List ヒープ = 新しいリスト (); int[] 値 = { 10, 7, 11, 5, 4, 13 }; foreach(値の int 値) { InsertMinHeap(ヒープ, 値); Console.Write('最小ヒープに ' + 値 + ' を挿入しました: '); foreach(ヒープ内の int 要素) { Console.Write(要素 + ' '); Console.WriteLine(); } } }>>'JavaScriptInserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...> 時間計算量: O(log(n)) ( ここで、n はヒープ内の要素の番号です。 )
補助スペース: の上)
2. 最小ヒープ データ構造の削除 :
最小ヒープから最小の要素 (ルート) を削除します。ルートはヒープ内の最後の要素に置き換えられ、親が両方の子よりも小さくなるか、新しいルートがリーフ ノードに到達するまで、新しいルートとその最小の子を交換することによってヒープ プロパティが復元されます。
- 削除するルートまたは要素を最後の要素に置き換えます。
- ヒープから最後の要素を削除します。
- 最後の要素がルート ノードの位置に配置されるようになりました。そのため、ヒープのプロパティに従わない可能性があります。したがって、ルートの位置に配置された最後のノードを山盛りにします。
図 :
ヒープが次のような最小ヒープであると仮定します。
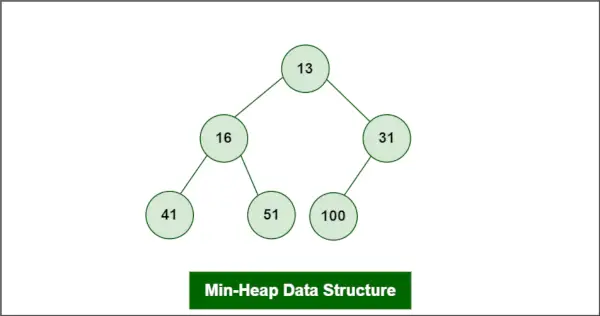
最小ヒープのデータ構造
Androidで誰かがあなたをブロックしたかどうかを確認する方法
削除する要素はルート、つまり 13 です。
プロセス :
最後の要素は 100 です。
ステップ1: 最後の要素をルートに置き換えて削除します。
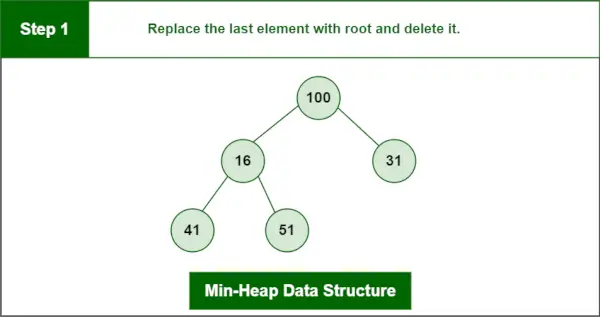
最小ヒープのデータ構造
ステップ2 : 根元を盛り上げます。
最終ヒープ:
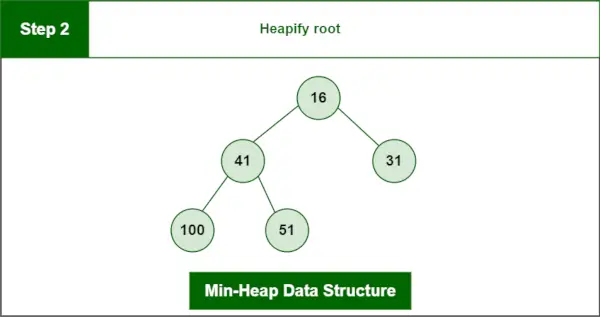
最小ヒープのデータ構造
Min-Heap での削除操作の実装:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // 新しい要素をヒープの最後に追加します heap.push_back(value); // 最後の要素のインデックスを取得 int index = heap.size() - 1; // 新しい要素をその親と比較し、 // 必要に応じて交換します while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // ツリーを現在の要素の親に移動します。 //index = (index - 1) / 2; } } // 最小ヒープからノードを削除する関数 void delete_min_heap(vector & heap, int value) { // 削除する要素のインデックスを検索 int index = -1; for (int i = 0; i< heap.size(); i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap[index] = heap[heap.size() - 1]; // Remove the last element heap.pop_back(); // Heapify the tree starting from the element at the // deleted index while (true) { int left_child = 2 * index + 1; int right_child = 2 * index + 2; int smallest = index; if (left_child < heap.size() && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.size() && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { swap(heap[index], heap[smallest]); index = smallest; } else { break; } } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() { vector ヒープ; int 値[] = { 13, 16, 31, 41, 51, 100 }; int n = sizeof(values) / sizeof(values[0]); for (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); } cout << 'Initial heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; delete_min_heap(heap, 13); cout << 'Heap after deleting 13: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; return 0; }>
ジャワ import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(List heap, int value) { // 新しい要素をヒープの末尾に追加します heap.add(value); // 最後の要素のインデックスを取得 int index = heap.size() - 1; // 新しい要素をその親と比較し、必要に応じて交換します // while (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap,index, (インデックス - 1) / 2); // ツリーを現在の要素の親に移動します。 //index = (index - 1) / 2; } } // 最小ヒープからノードを削除する関数 public static void deleteMinHeap(List heap, int value) { // 削除する要素のインデックスを検索します。 int index = -1; for (int i = 0; i< heap.size(); i++) { if (heap.get(i) == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap.set(index, heap.get(heap.size() - 1)); // Remove the last element heap.remove(heap.size() - 1); // Heapify the tree starting from the element at the // deleted index while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int smallest = index; if (leftChild < heap.size() && heap.get(leftChild) < heap.get(smallest)) { smallest = leftChild; } if (rightChild < heap.size() && heap.get(rightChild) < heap.get(smallest)) { smallest = rightChild; } if (smallest != index) { Collections.swap(heap, index, smallest); index = smallest; } else { break; } } } // Main function to test the insertMinHeap and // deleteMinHeap functions public static void main(String[] args) { List ヒープ = 新しい ArrayList (); int[] 値 = { 13, 16, 31, 41, 51, 100 }; int n = 値.長さ; for (int i = 0; i< n; i++) { insertMinHeap(heap, values[i]); } System.out.print('Initial heap: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); deleteMinHeap(heap, 13); System.out.print('Heap after deleting 13: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); } }> Python3 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 および heap[(index - 1) // 2]> heap[index]: heap[index], heap[(index - 1) // 2] = heap[(index - 1) // 2], heap[インデックス] インデックス = (インデックス - 1) // 2 def delete_min_heap(heap, value): インデックス = -1 for i in range(len(heap)): if heap[i] == value: インデックス = i ブレーク if インデックス== -1: heap[index] = heap[-1] heap.pop() を返します。 True の場合: left_child = 2 * インデックス + 1 right_child = 2 * インデックス + 2 最小 = インデックス if left_child< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)> C# using System; using System.Collections.Generic; class MinHeap { private List ヒープ = 新しいリスト (); public void Insert(int value) { heap.Add(value); int インデックス = heap.Count - 1; while (インデックス> 0 && ヒープ[(インデックス - 1) / 2]> ヒープ[インデックス]) { Swap(インデックス, (インデックス - 1) / 2); インデックス = (インデックス - 1) / 2; public void Delete(int value) { int インデックス = heap.IndexOf(value); if (インデックス == -1) { 戻り値; ヒープ[インデックス] = ヒープ[ヒープ.カウント - 1]; heap.RemoveAt(heap.Count - 1); while (true) { int leftChild = 2 * インデックス + 1; int rightChild = 2 * インデックス + 2; int 最小 = インデックス; if (左子< heap.Count && heap[leftChild] < heap[smallest]) { smallest = leftChild; } if (rightChild < heap.Count && heap[rightChild] < heap[smallest]) { smallest = rightChild; } if (smallest != index) { Swap(index, smallest); index = smallest; } else { break; } } } private void Swap(int i, int j) { int temp = heap[i]; heap[i] = heap[j]; heap[j] = temp; } public void Print() { for (int i = 0; i < heap.Count; i++) { Console.Write(heap[i] + ' '); } Console.WriteLine(); } } class Program { static void Main(string[] args) { MinHeap heap = new MinHeap(); int[] values = { 13, 16, 31, 41, 51, 100 }; for (int i = 0; i < values.Length; i++) { heap.Insert(values[i]); } Console.Write('Initial heap: '); heap.Print(); heap.Delete(13); Console.Write('Heap after deleting 13: '); heap.Print(); } }> JavaScript function insertMinHeap(heap, value) { // Add the new element to the end of the heap heap.push(value); // Get the index of the last element let index = heap.length - 1; // Compare the new element with its parent and swap if necessary for (let flr = Math.floor((index - 1) / 2); index>0 && ヒープ[flr]> ヒープ[インデックス]; flr = Math.floor((インデックス - 1) / 2)) { [ヒープ[インデックス], ヒープ[flr]] = [ヒープ[flr], ヒープ[インデックス], ]; // ツリーを現在の要素の親に移動します。index = Math.floor((index - 1) / 2); } } function deleteMinHeap(heap, value) { // 削除する要素のインデックスを検索します。 letindex = -1; for (i = 0 とする; i< heap.length; i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last element heap[index] = heap[heap.length - 1]; // Remove the last element heap.pop(); // Heapify the tree starting from the element at the deleted index while (true) { let left_child = 2 * index + 1; let right_child = 2 * index + 2; let smallest = index; if (left_child < heap.length && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.length && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { [heap[index], heap[smallest]] = [heap[smallest], heap[index]]; index = smallest; } else { break; } } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) { insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));>
出力 Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>
時間計算量 : O(log n) ここで、n はヒープ内の要素の数です。
補助スペース: の上)
3. Min-Heap データ構造に対するピーク操作:
最小要素 (つまり、ヒープのルート) にアクセスするには、ルート ノードの値が返されます。最小ヒープ内のピークの時間計算量は O(1) です。
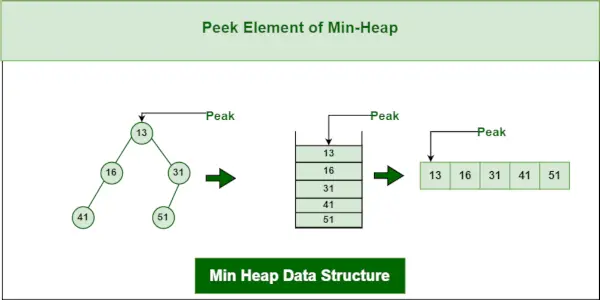
最小ヒープ データ構造
Min-Heap での Peek 操作の実装:
C++ #include #include #include using namespace std; int main() { // Create a max heap with some elements using a // priority_queue priority_queue 、より大きい > 最小ヒープ; minHeap.push(9); minHeap.push(8); minHeap.push(7); minHeap.push(6); minHeap.push(5); minHeap.push(4); minHeap.push(3); minHeap.push(2); minHeap.push(1); // ピーク要素 (つまり、最大の要素) を取得します int PeakElement = minHeap.top(); // ピーク要素 cout を出力します。<< 'Peak element: ' << peakElement << std::endl; return 0; }> ジャワ import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { // Create a max heap with some elements using a // PriorityQueue PriorityQueue minHeap = 新しい PriorityQueue(); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // ピーク要素 (つまり、最大の要素) を取得します int PeakElement = minHeap.peek(); // ピーク要素を出力します System.out.println('ピーク要素: ' + PeakElement); } }>> Python3 import heapq # Create a min heap with some elements using a list min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1] heapq.heapify(min_heap) # Get the peak element (i.e., the smallest element) peak_element = heapq.nsmallest(1, min_heap)[0] # Print the peak element print('Peak element:', peak_element)> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { // Create a min heap with some elements using a // PriorityQueue var minHeap = new PriorityQueue (); minHeap.Enqueue(9); minHeap.Enqueue(8); minHeap.Enqueue(7); minHeap.Enqueue(6); minHeap.Enqueue(5); minHeap.Enqueue(4); minHeap.Enqueue(3); minHeap.Enqueue(2); minHeap.Enqueue(1); // ピーク要素 (つまり、最小の要素) を取得します int PeakElement = minHeap.Peek(); // ピーク要素を出力します Console.WriteLine('ピーク要素: ' + PeakElement); } }>> JavaScript const PriorityQueue = require('fast-priority-queue'); // Create a min heap with some elements using a PriorityQueue const minHeap = new PriorityQueue((a, b) =>a - b); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // ピーク要素 (つまり、最小の要素) を取得します const PeakElement = minHeap.peek(); // ピーク要素を出力します console.log(`ピーク要素: ${peakElement}`);>>
出力 Peak element: 1>
時間計算量 : 配列またはリストを使用して実装された最小ヒープでは、ピーク要素は常にヒープのルートに位置するため、一定時間 O(1) でアクセスできます。
バイナリ ツリーを使用して実装された最小ヒープでは、ピーク要素は常にツリーのルートに位置するため、O(1) 時間でアクセスすることもできます。
補助スペース: の上)
4. Min-Heap データ構造に対する Heapify 操作:
heapify 操作を使用すると、ソートされていない配列から最小ヒープを作成できます。これは、最後の非リーフ ノードから開始して、すべてのノードがヒープ プロパティを満たすまでバブル ダウン操作を繰り返し実行することによって行われます。
最小ヒープでの Heapify 操作
Min-Heap での Heapify 操作の実装:
C++ #include #include using namespace std; void minHeapify(vector &arr, int i, int n) { int 最小 = i; int l = 2*i + 1; int r = 2*i + 2; もし(l< n && arr[l] < arr[smallest]) smallest = l; if (r < n && arr[r] < arr[smallest]) smallest = r; if (smallest != i) { swap(arr[i], arr[smallest]); minHeapify(arr, smallest, n); } } int main() { vector arr = {10, 5, 15, 2, 20, 30}; コート<< 'Original array: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; // Perform heapify operation on min-heap for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); コート<< '
Min-Heap after heapify operation: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; return 0; }>
ジャワ // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main { // Function to maintain the min-heap property of the heap rooted at index 'i' public static void minHeapify(List arr, int i, int n) { // 最初はルートが最小の要素であると仮定します。 int smallest = i; // 現在のノードの左右の子のインデックスを計算します int l = 2 * i + 1; int r = 2 * i + 2; // 左の子と現在の最小の子を比較します if (l< n && arr.get(l) < arr.get(smallest)) smallest = l; // Compare the right child with the current smallest if (r < n && arr.get(r) < arr.get(smallest)) smallest = r; // If the current node is not the smallest, swap it with the smallest child if (smallest != i) { int temp = arr.get(i); arr.set(i, arr.get(smallest)); arr.set(smallest, temp); // Recursively heapify the subtree rooted at the smallest child minHeapify(arr, smallest, n); } } public static void main(String[] args) { // Create a list representing the array List arr = Arrays.asList(10, 5, 15, 2, 20, 30); System.out.print('元の配列: '); // 元の配列を出力します (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); // Perform heapify operation on the min-heap // Start from the last non-leaf node and go up to the root of the tree for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); System.out.print('
ヒープ化操作後の最小ヒープ: '); // heapify 操作後の最小ヒープを出力します。 for (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); } }> パイソン def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)> C# using System; using System.Collections.Generic; class GFG { // Function to perform the minHeapify operation on a min-heap. static void MinHeapify(List arr、int i、int n) { int 最小 = i; int left = 2 * i + 1; int right = 2 * i + 2; // 左側の子と現在の最小ノードを比較します。 もし(左)< n && arr[left] < arr[smallest]) smallest = left; // Compare the right child with the current smallest node. if (right < n && arr[right] < arr[smallest]) smallest = right; // If the current node is not the smallest // swap it with the smallest child. if (smallest != i) { int temp = arr[i]; arr[i] = arr[smallest]; arr[smallest] = temp; // Recursively call minHeapify on the affected subtree. MinHeapify(arr, smallest, n); } } static void Main(string[] args) { List arr = 新しいリスト { 10、5、15、2、20、30 }; Console.Write('元の配列: '); foreach (arr の int num) Console.Write(num + ' '); // 最小ヒープに対してヒープ化操作を実行します。 for (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count); Console.Write('
ヒープ化操作後の最小ヒープ: '); foreach (arr の int num) Console.Write(num + ' '); } }>> JavaScript // Define a function to perform min-heapify operation on an array function minHeapify(arr, i, n) { let smallest = i; let l = 2 * i + 1; let r = 2 * i + 2; // Check if left child is smaller than the current smallest element if (l < n && arr[l] < arr[smallest]) smallest = l; // Check if right child is smaller than the current smallest element if (r < n && arr[r] < arr[smallest]) smallest = r; // If the smallest element is not the current element, swap them if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]]; minHeapify(arr, smallest, n); } } // Main function function main() { const arr = [10, 5, 15, 2, 20, 30]; // Print the original array console.log('Original array: ' + arr.join(' ')); // Perform heapify operation on the min-heap for (let i = Math.floor(arr.length / 2) - 1; i>= 0; i--) minHeapify(arr, i, arr.length); // heapify 操作後の最小ヒープを出力します console.log('heapify 操作後の最小ヒープ: ' + arr.join(' ')); } // main 関数を呼び出してプロセスを開始します main();>>
出力 Original array: 10 5 15 2 20 30 Min-Heap after heapify operation: 2 5 15 10 20 30>
最小ヒープ内の heapify の時間計算量は O(n) です。
5. Min-Heap データ構造の検索操作:
最小ヒープ内の要素を検索するには、ヒープを表す配列に対して線形検索を実行できます。ただし、線形探索の時間計算量は O(n) であり、効率的ではありません。したがって、検索は最小ヒープ内で一般的に使用される操作ではありません。
以下は、最小ヒープ内の要素を検索する方法を示すコード例です。 std::find() :
C++ #include using namespace std; int main() { priority_queue 、より大きい > 最小ヒープ; // 最大ヒープの例 min_heap.push(10); min_heap.push(9); min_heap.push(8); min_heap.push(6); min_heap.push(4); int 要素 = 6; // 検索する要素 bool found = false; // 最小ヒープを一時キューにコピーし、 // 要素 std::priority_queue を検索します 、より大きい > 温度 = 最小ヒープ; while (!temp.empty()) { if (temp.top() == 要素) { found = true; 壊す; temp.pop(); if (見つかった) { std::cout<< 'Element found in the min heap.' << std::endl; } else { std::cout << 'Element not found in the min heap.' << std::endl; } return 0; }> ジャワ import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { PriorityQueue min_heap = 新しい PriorityQueue(); min_heap.add(3); // 要素を優先キューに挿入します min_heap.offer(1); min_heap.offer(4); min_heap.offer(1); min_heap.offer(6); int 要素 = 6; // 検索する要素 boolean found = false; // 最小ヒープを一時キューにコピーし、 // 要素 PriorityQueue を検索します temp = 新しい PriorityQueue(min_heap); while (!temp.isEmpty()) { if (temp.poll() == 要素) { found = true; 壊す; if (found) { System.out.println( '最小ヒープで要素が見つかりました。'); } else { System.out.println( '要素が最小ヒープに見つかりません。'); } } }>>'Python3 C# using System; using System.Collections.Generic; public class GFG { public static void Main() { var minHeap = new PriorityQueue (); // 最小ヒープの例 minHeap.Enqueue(4); minHeap.Enqueue(6); minHeap.Enqueue(8); minHeap.Enqueue(9); minHeap.Enqueue(10); int 要素 = 6; // 検索する要素 bool found = false; // 最小ヒープを一時キューにコピーし、 // 要素を検索します var temp = new PriorityQueue (minHeap); while (temp.Count> 0) { if (temp.Peek() == 要素) { found = true; 壊す; temp.Dequeue(); if (found) { Console.WriteLine( '最小ヒープで要素が見つかりました。'); } else { Console.WriteLine( '要素が最小ヒープに見つかりません。'); } } }>>'JavaScript>
出力 Element found in the min heap.>
複雑さの分析 :
の 時間の複雑さ このプログラムのは O(n log n) 、 どこ n 優先キュー内の要素の数です。
挿入操作の時間計算量は次のとおりです。 O(log n) 最悪の場合、ヒーププロパティを維持する必要があるためです。検索操作には、優先キューを一時キューにコピーし、次に一時キューを走査することが含まれます。 O(n log n) 各要素をコピーしてキューからポップする必要があり、操作ごとに優先キューを再構築する必要があるため、最悪の場合は時間がかかります。
の 空間の複雑さ プログラムの の上) 保管しているので n 優先キュー内の要素を使用して一時キューを作成します。 n 要素。
最小ヒープ データ構造のアプリケーション:
- ヒープソート: 最小ヒープは、時間計算量が O(nlogn) の効率的なソート アルゴリズムであるヒープ ソート アルゴリズムの主要なコンポーネントとして使用されます。
- 優先キュー: 優先キューは、最小値を持つ要素が常にルートにある最小ヒープ データ構造を使用して実装できます。
- ダイクストラのアルゴリズム: ダイクストラのアルゴリズムでは、開始頂点からの距離が最小のグラフの頂点を格納するために最小ヒープが使用されます。最小距離の頂点は常にヒープのルートにあります。
- ハフマン符号化: ハフマン コーディングでは、最小ヒープを使用して優先キューを実装し、特定の文字セットに最適なプレフィックス コードを構築します。
- K 個のソートされた配列をマージします。 K 個のソートされた配列が与えられた場合、最小ヒープ データ構造を使用して、それらを 1 つのソートされた配列に効率的にマージできます。
最小ヒープ データ構造の利点:
- 効率的な挿入と削除 : 最小ヒープでは、O(log n) の時間計算量で要素を高速に挿入および削除できます。ここで、n はヒープ内の要素の数です。
- 最小要素の効率的な取得: 最小ヒープ内の最小要素は常にヒープのルートにあり、O(1) 時間で取得できます。
- スペース効率: 最小ヒープは、配列またはバイナリ ツリーを使用して実装できるコンパクトなデータ構造であり、スペース効率が高くなります。
- 並べ替え: 最小ヒープを使用すると、時間計算量が O(n log n) のヒープ ソートなどの効率的なソート アルゴリズムを実装できます。
- 優先キュー: 最小ヒープを使用して優先度キューを実装すると、最小優先度を持つ要素を O(1) 時間で効率的に取得できます。
- 多用途性: Min ヒープには、グラフ アルゴリズム、データ圧縮、データベース システムなど、コンピューター サイエンスの分野でいくつかの用途があります。
全体として、min heap は、効率的な操作とスペース効率を提供し、コンピューター サイエンスでいくつかの用途がある便利で多用途のデータ構造です。




