R プログラミングのロジスティック回帰は、イベントの成功と失敗の確率を見つけるために使用される分類アルゴリズムです。ロジスティック回帰は、従属変数が本質的にバイナリ (0/1、True/False、Yes/No) である場合に使用されます。ロジット関数は、二項分布のリンク関数として使用されます。
バイナリ結果変数の確率は、ロジスティック回帰として知られる統計モデリング手法を使用して予測できます。マーケティング、金融、社会科学、医学研究など、さまざまな業界で広く採用されています。
ロジスティック関数は一般にシグモイド関数と呼ばれ、ロジスティック回帰を支える基本的な考え方です。このシグモイド関数は、予測変数とバイナリ結果の尤度の間の相関関係を記述するためにロジスティック回帰で使用されます。

R プログラミングにおけるロジスティック回帰
ロジスティック回帰は次のようにも知られています。 二項ロジスティクス回帰 。これは、出力が確率であり、入力が -無限大から + 無限大までのシグモイド関数に基づいています。
理論
ロジスティック回帰は、一般化線形モデルとしても知られています。定性的応答を予測するための分類手法として使用されるため、y の値は 0 から 1 の範囲であり、次の方程式で表すことができます。

R プログラミングにおけるロジスティック回帰
p は、対象の特性の確率です。オッズ比は、失敗の確率と比較した成功の確率として定義されます。これはロジスティック回帰係数の重要な表現であり、0 から無限大までの値を取ることができます。オッズ比 1 は、成功の確率が失敗の確率と等しい場合です。オッズ比 2 は、成功の確率が失敗の確率の 2 倍である場合です。オッズ比 0.5 は、失敗の確率が成功の確率の 2 倍である場合です。
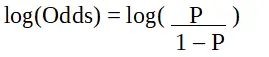
R プログラミングにおけるロジスティック回帰
二項分布(従属変数)を使用しているため、この分布に最適なリンク関数を選択する必要があります。
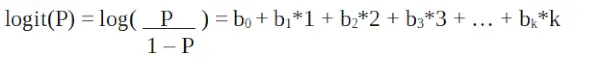
R プログラミングにおけるロジスティック回帰
それは ロジット関数 。上の式では、(通常の回帰のように) 二乗誤差の合計を最小化するのではなく、サンプル値を観察する可能性を最大化するために括弧が選択されています。ロジットはオッズの対数とも呼ばれます。ロジット関数は独立変数と線形関係にある必要があります。これは方程式 A からのもので、左側は x の線形結合です。これは、y が x に線形関係があるという OLS の仮定に似ています。変数 b0、b1、b2 などは不明なので、利用可能なトレーニング データに基づいて推定する必要があります。ロジスティック回帰モデルでは、b1 に 1 単位を乗算すると、ロジットが b0 だけ変化します。 1 単位の変化による P の変化は、乗算される値によって異なります。 b1 が正の場合、P は増加し、b1 が負の場合、P は減少します。
データセット
MTカー (モーター トレンド カー ロード テスト) は、32 台の自動車の燃費、パフォーマンス、および自動車設計の 10 の側面で構成されます。プリインストールされています dplyr Rのパッケージ。
R
# Installing the package> install.packages>(>'dplyr'>)> # Loading package> library>(dplyr)> # Summary of dataset in package> summary>(mtcars)> |
>
>
データセットに対してロジスティック回帰を実行する
ロジスティック回帰は、R で次のように実装されます。 glm() データセット内の特徴または変数を使用してモデルをトレーニングすることによって。
R
# Installing the package> # For Logistic regression> install.packages>(>'caTools'>)> # For ROC curve to evaluate model> install.packages>(>'ROCR'>)> > # Loading package> library>(caTools)> library>(ROCR)> |
>
>
データの分割
R
# Splitting dataset> split <->sample.split>(mtcars, SplitRatio = 0.8)> split> train_reg <->subset>(mtcars, split ==>'TRUE'>)> test_reg <->subset>(mtcars, split ==>'FALSE'>)> # Training model> logistic_model <->glm>(vs ~ wt + disp,> >data = train_reg,> >family =>'binomial'>)> logistic_model> # Summary> summary>(logistic_model)> |
>
>
出力:
Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (切片) 1.58781 2.60087 0.610 0.5415 wt 1.36958 1.60524 0.853 0.3936 disp -0.02969 0.01577 -1.882 0.0598 。 --- シニフ。コード: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (二項族の分散パラメータを 1 とみなします) ヌル逸脱: 24 自由度で 34.617 残留逸脱: 20.212 22 自由度 AIC: 26.212 フィッシャー スコアリング反復数: 6>>
- 呼び出し: ロジスティック回帰モデルを近似するために使用される関数呼び出しが、ファミリー、式、およびデータに関する情報とともに表示されます。逸脱残差: これらは逸脱残差であり、モデルの適合度を測定します。これらは、実際の応答とロジスティック回帰モデルによって予測される確率との間の差異を表します。係数: ロジスティック回帰におけるこれらの係数は、応答変数の対数オッズまたはロジットを表します。推定された係数に関連する標準誤差は、Std.に示されています。エラー列。有意性コード: 各予測変数の有意性レベルは、有意性コードによって示されます。分散パラメータ: ロジスティック回帰では、分散パラメータは二項分布のスケーリング パラメータとして機能します。このインスタンスでは 1 に設定されており、想定される分散が 1 であることを示します。 ヌル逸脱: ヌル逸脱は、切片のみを考慮した場合のモデルの偏差を計算します。これは、予測変数のないモデルから生じる偏差を象徴しています。残差逸脱: 残差逸脱は、予測変数が適合された後のモデルの偏差を計算します。これは、予測変数を考慮した後の残差偏差を表します。 AIC: 赤池情報量基準 (AIC) は、予測変数の数を考慮したもので、モデルの適合度を測る尺度です。過剰適合を防ぐために、より複雑なモデルにペナルティを与えます。より適合したモデルは、AIC 値が低いほど示されます。フィッシャー スコアリングの反復数: モデル パラメーターを推定するためにフィッシャー スコアリング手順で必要な反復数は、反復数によって示されます。
モデルに基づいてテストデータを予測する
R
雪と氷
predict_reg <->predict>(logistic_model,> >test_reg, type =>'response'>)> predict_reg> |
>
>
出力:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943>
R
# Changing probabilities> predict_reg <->ifelse>(predict_reg>0.5、1、0)>> # Evaluating model accuracy> # using confusion matrix> table>(test_reg$vs, predict_reg)> missing_classerr <->mean>(predict_reg != test_reg$vs)> print>(>paste>(>'Accuracy ='>, 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <->prediction>(predict_reg, test_reg$vs)> ROCPer <->performance>(ROCPred, measure =>'tpr'>,> >x.measure =>'fpr'>)> auc <->performance>(ROCPred, measure =>'auc'>)> auc <- [email protected][[1]]> auc> # Plotting curve> plot>(ROCPer)> plot>(ROCPer, colorize =>TRUE>,> >print.cutoffs.at =>seq>(0.1, by = 0.1),> >main =>'ROC CURVE'>)> abline>(a = 0, b = 1)> auc <->round>(auc, 4)> legend>(.6, .4, auc, title =>'AUC'>, cex = 1)> |
>
>
出力:
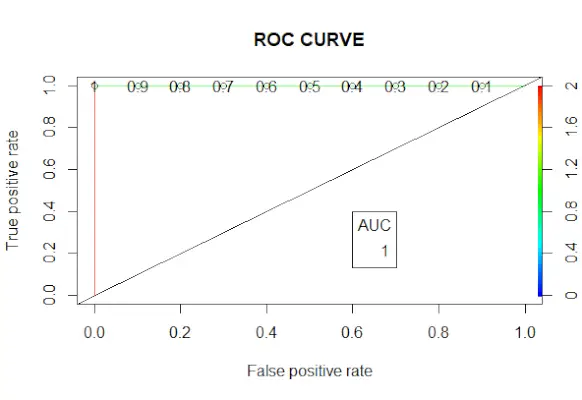
ROC カーブ
例 2:
R で設定されたロジスティック回帰モデルの Titanic Data を実行できます。
R
# Load the dataset> data>(Titanic)> # Convert the table to a data frame> data <->as.data.frame>(Titanic)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary>(model)> |
>
>
出力:
Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (インターセプト) 4.022e-16 8.660e-01 0 1 Class2nd -9.762e-16 1.000e+00 0 1 Class3rd -4.699e-16 1.000e+00 0 1 ClassCrew -5.551e-16 1.000e+ 00 0 1 Sex Female -3.140e-16 7.071e-01 0 1 AgeAdult 5.103e-16 7.071e-01 0 1 (二項族の分散パラメーターを 1 とみなします) ヌル逸脱: 31 自由度での 44.361 残留逸脱: 44.361 26 自由度の場合 AIC: 56.361 フィッシャー スコアリングの反復数: 2>>
タイタニック号データセットの ROC 曲線をプロットする
R
# Install and load the required packages> install.packages>(>'ROCR'>)> library>(ROCR)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <->predict>(model, type =>'response'>)> # Create a prediction object for ROCR> prediction_objects <->prediction>(predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <->performance>(prediction_obj, measure =>'tpr'>, x.measure =>'fpr'>)> # Plot the ROC curve> plot>(roc_object, main =>'ROC Curve'>, col =>'blue'>, lwd = 2)> # Add labels and a legend to the plot> legend>(>'bottomright'>, legend => >paste>(>'AUC ='>,>round>(>performance>(prediction_objects, measure =>'auc'>)> >@y.values[[1]], 2)), col =>'blue'>, lwd = 2)> |
>
>
出力:
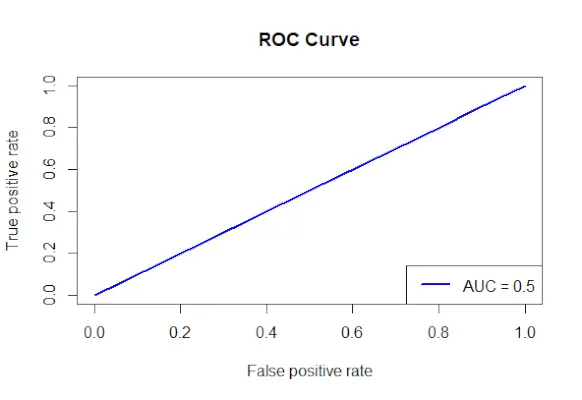
ROC曲線
- Survived の予測に使用される要素が指定され、Survived Class + Sex + Age という式を使用してロジスティック回帰モデルが作成されます。
- detect() 関数を使用すると、適合モデルを使用してデータセットに対して予測が行われます。
- ROCR パッケージの予測() メソッドを使用して、予測確率を実際の結果値と組み合わせて予測オブジェクトを構築します。
- 真陽性率 (tpr) の測定値と偽陽性率 (fpr) の x 軸測定値が指定され、ROCR パッケージのパフォーマンス() 関数を使用して ROC 曲線オブジェクトが作成されます。
- メインタイトル、色、線幅を指定する ROC 曲線オブジェクト (roc_obj) は、plot() 関数を使用してプロットされます。
- これは、measure = auc を指定した Performance() 関数を使用して AUC (曲線下面積) 値を決定し、プロットにラベルと凡例を追加します。
