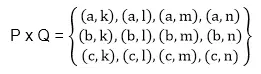和集合、積集合、補集合の操作に基づく集合は、表 1 に示すさまざまな法則 (恒等式) を満たします。

表: 集合代数の法則

表 1 は集合の代数の法則を示しています。

例 1: 冪等法則を証明する:

 (a) A ∪ A = A 

解決：

 Since, B ⊂ A ∪ B, therefore A ⊂ A ∪ A Let x ∈ A ∪ A ⇒ x ∈ A or x ∈ A ⇒ x ∈ A ∴ A ∪ A ⊂ A As A ∪ A ⊂ A and A ⊂ A ∪ A ⇒ A =A ∪ A. Hence Proved. 

 (b) A ∩ A = A 

解決：

 Since, A ∩ B ⊂ B, therefore A ∩ A ⊂ A Let x ∈ A ⇒ x ∈ A and x ∈ A ⇒ x ∈ A ∩ A ∴ A ⊂ A ∩ A As A ∩ A ⊂ A and A ⊂ A ∩ A ⇒ A = A ∩ A. Hence Proved. 

例 2: 結合法則を証明する:

 (a) (A ∪ B) ∪ C = A ∪ (B ∪ C) 

解決：

 Let some x ∈ (A'∪ B) ∪ C ⇒ (x ∈ A or x ∈ B) or x ∈ C ⇒ x ∈ A or x ∈ B or x ∈ C ⇒ x ∈ A or (x ∈ B or x ∈ C) ⇒ x ∈ A or x ∈ B ∪ C ⇒ x ∈ A ∪ (B ∪ C). Similarly, if some x ∈ A ∪ (B ∪ C), then x ∈ (A ∪ B) ∪ C. Thus, any x ∈ A ∪ (B ∪ C) ⇔ x ∈ (A ∪ B) ∪ C. Hence Proved. 

 (b) (A ∩ B) ∩ C = A ∩ (B ∩ C) 

解決：

 Let some x ∈ A ∩ (B ∩ C) ⇒ x ∈ A and x ∈ B ∩ C ⇒ x ∈ A and (x ∈ B and x ∈ C) ⇒ x ∈ A and x ∈ B and x ∈ C ⇒ (x ∈ A and x ∈ B) and x ∈ C) ⇒ x ∈ A ∩ B and x ∈ C ⇒ x ∈ (A ∩ B) ∩ C. Similarly, if some x ∈ A ∩ (B ∩ C), then x ∈ (A ∩ B) ∩ C Thus, any x ∈ (A ∩ B) ∩ C ⇔ x ∈ A ∩ (B ∩ C). Hence Proved. 

例 3: 交換法則の証明

 (a) A ∪ B = B ∪ A 

解決：

 To Prove A ∪ B = B ∪ A A ∪ B = {x: x ∈ A or x ∈ B} = {x: x ∈ B or x ∈ A} (∵ Order is not preserved in case of sets) A ∪ B = B ∪ A. Hence Proved. 

 (b) A ∩ B = B ∩ A 

解決：

 To Prove A ∩ B = B ∩ A A ∩ B = {x: x ∈ A and x ∈ B} = {x: x ∈ B and x ∈ A} (∵ Order is not preserved in case of sets) A ∩ B = B ∩ A. Hence Proved. 

例 4: 分配法則の証明

 (a) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) 

解決：

 To Prove Let x ∈ A ∪ (B ∩ C) ⇒ x ∈ A or x ∈ B ∩ C ⇒ (x ∈ A or x ∈ A) or (x ∈ B and x ∈ C) ⇒ (x ∈ A or x ∈ B) and (x ∈ A or x ∈ C) ⇒ x ∈ A ∪ B and x ∈ A ∪ C ⇒ x ∈ (A ∪ B) ∩ (A ∪ C) Therefore, A ∪ (B ∩ C) ⊂ (A ∪ B) ∩ (A ∪ C)............(i) Again, Let y ∈ (A ∪ B) ∩ (A ∪ C) ⇒ y ∈ A ∪ B and y ∈ A ∪ C ⇒ (y ∈ A or y ∈ B) and (y ∈ A or y ∈ C) ⇒ (y ∈ A and y ∈ A) or (y ∈ B and y ∈ C) ⇒ y ∈ A or y ∈ B ∩ C ⇒ y ∈ A ∪ (B ∩ C) Therefore, (A ∪ B) ∩ (A ∪ C) ⊂ A ∪ (B ∩ C)............(ii) Combining (i) and (ii), we get A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C). Hence Proved 

 (b) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) 

解決：

 To Prove Let x ∈ A ∩ (B ∪ C) ⇒ x ∈ A and x ∈ B ∪ C ⇒ (x ∈ A and x ∈ A) and (x ∈ B or x ∈ C) ⇒ (x ∈ A and x ∈ B) or (x ∈ A and x ∈ C) ⇒ x ∈ A ∩ B or x ∈ A ∩ C ⇒ x ∈ (A ∩ B) ∪ (A ∪ C) Therefore, A ∩ (B ∪ C) ⊂ (A ∩ B) ∪ (A ∪ C)............ (i) Again, Let y ∈ (A ∩ B) ∪ (A ∪ C) ⇒ y ∈ A ∩ B or y ∈ A ∩ C ⇒ (y ∈ A and y ∈ B) or (y ∈ A and y ∈ C) ⇒ (y ∈ A or y ∈ A) and (y ∈ B or y ∈ C) ⇒ y ∈ A and y ∈ B ∪ C ⇒ y ∈ A ∩ (B ∪ C) Therefore, (A ∩ B) ∪ (A ∪ C) ⊂ A ∩ (B ∪ C)............ (ii) Combining (i) and (ii), we get A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∪ C). Hence Proved 

例 5: ド・モルガンの法則を証明する

 (a) (A &#x222A;B)<sup>c</sup>=A<sup>c</sup>&#x2229; B<sup>c</sup> 

解決：

 To Prove (A &#x222A;B)<sup>c</sup>=A<sup>c</sup>&#x2229; B<sup>c</sup> Let x &#x2208; (A &#x222A;B)<sup>c</sup> &#x21D2; x &#x2209; A &#x222A; B (&#x2235; a &#x2208; A &#x21D4; a &#x2209; A<sup>c</sup>) &#x21D2; x &#x2209; A and x &#x2209; B &#x21D2; x &#x2209; A<sup>c</sup> and x &#x2209; B<sup>c</sup> &#x21D2; x &#x2209; A<sup>c</sup>&#x2229; B<sup>c</sup> Therefore, (A &#x222A;B)<sup>c</sup> &#x2282; A<sup>c</sup>&#x2229; B<sup>c</sup>............. (i) Again, let x &#x2208; A<sup>c</sup>&#x2229; B<sup>c</sup> &#x21D2; x &#x2208; A<sup>c</sup> and x &#x2208; B<sup>c</sup> &#x21D2; x &#x2209; A and x &#x2209; B &#x21D2; x &#x2209; A &#x222A; B &#x21D2; x &#x2208; (A &#x222A;B)<sup>c</sup> Therefore, A<sup>c</sup>&#x2229; B<sup>c</sup> &#x2282; (A &#x222A;B)<sup>c</sup>............. (ii) Combining (i) and (ii), we get A<sup>c</sup>&#x2229; B<sup>c</sup> =(A &#x222A;B)<sup>c</sup>. Hence Proved. 

 (b) (A &#x2229;B)<sup>c</sup> = A<sup>c</sup>&#x222A; B<sup>c</sup> 

解決：

 Let x &#x2208; (A &#x2229;B)<sup>c</sup> &#x21D2; x &#x2209; A &#x2229; B (&#x2235; a &#x2208; A &#x21D4; a &#x2209; A<sup>c</sup>) &#x21D2; x &#x2209; A or x &#x2209; B &#x21D2; x &#x2208; A<sup>c</sup> and x &#x2208; B<sup>c</sup> &#x21D2; x &#x2208; A<sup>c</sup>&#x222A; B<sup>c</sup> &#x2234; (A &#x2229;B)<sup>c</sup>&#x2282; (A &#x222A;B)<sup>c</sup>.................. (i) Again, Let x &#x2208; A<sup>c</sup>&#x222A; B<sup>c</sup> &#x21D2; x &#x2208; A<sup>c</sup> or x &#x2208; B<sup>c</sup> &#x21D2; x &#x2209; A or x &#x2209; B &#x21D2; x &#x2209; A &#x2229; B &#x21D2; x &#x2208; (A &#x2229;B)<sup>c</sup> &#x2234; A<sup>c</sup>&#x222A; B<sup>c</sup>&#x2282; (A &#x2229;B)<sup>c</sup>.................... (ii) Combining (i) and (ii), we get(A &#x2229;B)<sup>c</sup>=A<sup>c</sup>&#x222A; B<sup>c</sup>. Hence Proved. 

例 6: アイデンティティの法則を証明する。

 (a) A ∪ ∅ = A 

解決：

 To Prove A ∪ ∅ = A Let x ∈ A ∪ ∅ ⇒ x ∈ A or x ∈ ∅ ⇒ x ∈ A (∵x ∈ ∅, as ∅ is the null set ) Therefore, x ∈ A ∪ ∅ ⇒ x ∈ A Hence, A ∪ ∅ ⊂ A. We know that A ⊂ A ∪ B for any set B. But for B = ∅, we have A ⊂ A ∪ ∅ From above, A ⊂ A ∪ ∅ , A ∪ ∅ ⊂ A ⇒ A = A ∪ ∅. Hence Proved. 

 (b) A ∩ ∅ = ∅ 

解決：

 To Prove A ∩ ∅ = ∅ If x ∈ A, then x ∉ ∅ (∵∅ is a null set) Therefore, x ∈ A, x ∉ ∅ ⇒ A ∩ ∅ = ∅. Hence Proved. 

 (c) A ∪ U = U 

解決：

 To Prove A ∪ U = U Every set is a subset of a universal set. ∴ A ∪ U ⊆ U Also, U ⊆ A ∪ U Therefore, A ∪ U = U. Hence Proved. 

 (d) A ∩ U = A 

解決：

 To Prove A ∩ U = A We know A ∩ U ⊂ A................. (i) So we have to show that A ⊂ A ∩ U Let x ∈ A ⇒ x ∈ A and x ∈ U (∵ A ⊂ U so x ∈ A ⇒ x ∈ U ) ∴ x ∈ A ⇒ x ∈ A ∩ U ∴ A ⊂ A ∩ U................. (ii) From (i) and (ii), we get A ∩ U = A. Hence Proved. 

例 7: 補則の証明

 (a) A &#x222A; A<sup>c</sup>= U 

解決：

 To Prove A &#x222A; A<sup>c</sup>= U Every set is a subset of U &#x2234; A &#x222A; A<sup>c</sup> &#x2282; U.................. (i) We have to show that U &#x2286; A &#x222A; A<sup>c</sup> Let x &#x2208; U &#x21D2; x &#x2208; A or x &#x2209; A &#x21D2; x &#x2208; A or x &#x2208; A<sup>c</sup> &#x21D2; x &#x2208; A &#x222A; A<sup>c</sup> &#x2234; U &#x2286; A &#x222A; A<sup>c</sup>................... (ii) From (i) and (ii), we get A &#x222A; A<sup>c</sup>= U. Hence Proved. 

 (b) A &#x2229; A<sup>c</sup>=&#x2205; 

解決：

 As &#x2205; is the subset of every set &#x2234; &#x2205; &#x2286; A &#x2229; A<sup>c</sup>..................... (i) We have to show that A &#x2229; A<sup>c</sup> &#x2286; &#x2205; Let x &#x2208; A &#x2229; A<sup>c</sup> &#x21D2; x &#x2208; A and x &#x2208; A<sup>c</sup> &#x21D2; x &#x2208; A and x &#x2209; A &#x21D2; x &#x2208; &#x2205; &#x2234; A &#x2229; A<sup>c</sup> &#x2282;&#x2205;..................... (ii) From (i) and (ii), we get A&#x2229; A<sup>c</sup>=&#x2205;. Hence Proved. 

 (c) U<sup>c</sup>= &#x2205; 

解決：

 Let x &#x2208; U<sup>c</sup> &#x21D4; x &#x2209; U &#x21D4; x &#x2208; &#x2205; &#x2234; U<sup>c</sup>= &#x2205;. Hence Proved. (As U is the Universal Set). 

 (d) &#x2205;<sup>c</sup> = U 

解決：

 Let x &#x2208; &#x2205;<sup>c</sup> &#x21D4; x &#x2209; &#x2205; &#x21D4; x &#x2208; U (As &#x2205; is an empty set) &#x2234; &#x2205;<sup>c</sup> = U. Hence Proved. 

例8: インボリューションの法則の証明

 (a) (A<sup>c</sup> )<sup>c</sup> A. 

解決：

 Let x &#x2208; (A<sup>c</sup> )<sup>c</sup> &#x21D4; x &#x2209; A<sup>c</sup>&#x21D4; x &#x2208; a &#x2234; (A<sup>c</sup> )<sup>c</sup> =A. Hence Proved. 

二重性:

E の双対 E∗ は、E に出現するすべての ∪、∩、U、∅ をそれぞれ ∩、∪、∅、U に置き換えることによって得られる式です。たとえば、次の双対

 (U ∩ A) ∪ (B ∩ A) = A is (∅ ∪ A) ∩ (B ∪ A) = A 

双対性の原理として、方程式 E が単位である場合、その双対 E∗ も単位であることが注目されます。

拡張の原則:

拡張の原則によると、2 つのセット A と B は、同じメンバーを持つ場合にのみ同じになります。等しい集合を A=B で表します。

 If A= {1, 3, 5} and B= {3, 1, 5}, then A=B i.e., A and B are equal sets. If A= {1, 4, 7} and B= {5, 4, 8}, then A≠ B i.e.., A and B are unequal sets. 

2 つの集合のデカルト積:

2 つの集合 P と Q の順序でのデカルト積は、最初のメンバーが集合 P に属し、2 番目のメンバーが集合 Q に属するすべての順序付きペアの集合であり、P x Q で表されます。

1から10までの乱数

 P x Q = {(x, y): x ∈ P, y ∈ Q}. 

例： P = {a, b, c} および Q = {k, l, m, n} とします。 P と Q のデカルト積を求めます。

解決： P と Q のデカルト積は次のようになります。