- 私たちは前方または後方のいずれかで推論できる戦略を研究しましたが、複雑で大きな問題を解決するには 2 つの方向を組み合わせた方が適切です。このような混合戦略により、最初に問題の主要な部分を解決し、その後、問題の主要な部分を組み合わせるときに発生する小さな問題に戻って解決することが可能になります。このようなテクニックはと呼ばれます 手段目的分析 。
- 手段目的分析は、AI プログラムの検索を制限するために人工知能で使用される問題解決手法です。
- これは、後方検索技術と前方検索技術を組み合わせたものです。
- MEA 技術は、1961 年にアレン ニューウェルとハーバート A. サイモンによって、一般問題ソルバー (GPS) と名付けられた問題解決コンピュータ プログラムに初めて導入されました。
- MEA 分析プロセスは、現在の状態と目標状態の間の差異の評価を中心としていました。
手段目的分析の仕組み:
手段目的分析プロセスは、問題に対して再帰的に適用できます。問題解決において検索をコントロールする戦略です。以下は、問題を解決するための MEA 技術の動作を説明する主なステップです。
- まず、初期状態と最終状態の違いを評価します。
- それぞれの違いに適用できるさまざまな演算子を選択します。
- それぞれの差に演算子を適用すると、現在の状態と目標状態の差が小さくなります。
オペレーターのサブゴール
MEA プロセスでは、現在の状態と目標の状態の違いを検出します。これらの違いが発生したら、演算子を適用して違いを減らすことができます。ただし、演算子を現在の状態に適用できない場合があります。したがって、演算子を適用できる現在の状態の部分問題を作成します。演算子が選択され、演算子の前提条件を確立するためにサブ目標が設定されるこのようなタイプの後向き連鎖は、と呼ばれます。 オペレーターのサブゴール 。
手段目的分析のアルゴリズム:
現在の状態を CURRENT 、目標の状態を GOAL として、MEA アルゴリズムの手順を次に示します。
OSIモデルレイヤー
- 現在の差に適用できる新しい演算子 O を選択し、そのような演算子がない場合は失敗を通知します。
- 演算子 O を CURRENT に適用してみます。 2 つの状態について説明します。
i) O-Start、O の前提条件が満たされた状態。
ii) O-Result、O-start で O が適用された場合に生じる状態。 - もし
(前編)<------ mea (current, o-start)< strong>
そして
(最後の部分<----- mea (o-result, goal)< strong>、成功した場合は、成功を通知し、FIRST-PART、O、および LAST-PART を組み合わせた結果を返します。
上で説明したアルゴリズムは単純な問題に適していますが、複雑な問題を解決するには適切ではありません。
平均目標分析の例:
以下に示すように初期状態と目標状態がわかっている例を考えてみましょう。この問題では、初期状態と目標状態の違いを見つけて演算子を適用することで、目標状態を取得する必要があります。
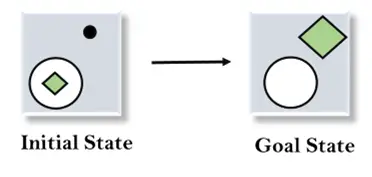
解決:
上記の問題を解決するには、まず初期状態と目標状態の違いを見つけ、それぞれの違いに対して新しい状態を生成し、演算子を適用します。この問題に対して使用できる演算子は次のとおりです。
Wordの透かし
1. 初期状態の評価: 最初のステップでは、初期状態を評価し、初期状態と目標状態を比較して、両方の状態の違いを見つけます。
Javaの文字列で

2. 削除演算子の適用: 確認できるように、最初の違いは、目標状態には初期状態に存在するドット シンボルがないことです。そのため、最初に 演算子の削除 このドットを削除するには、

3. 移動演算子の適用: 削除演算子を適用すると、新しい状態が発生します。これを再び目標状態と比較します。これらの状態を比較すると、正方形が円の外側にあるという別の違いがあるため、 移動オペレータ 。

4. 展開演算子の適用: 3 番目のステップで新しい状態が生成され、この状態を目標の状態と比較します。州を比較した後も、正方形のサイズという違いが 1 つあるため、次のように適用します。 展開演算子 , そして最後に、目標状態を生成します。

