現実世界では 機械学習 アプリケーションでは、関連する機能が多数あるのが一般的ですが、それらのサブセットのみが観察可能である場合があります。観測できる場合もあれば観測できない場合もある変数を扱う場合、その変数が可視または観測されているときにインスタンスを利用して、観測できないインスタンスを学習して予測することが実際に可能です。このアプローチは、欠損データの処理と呼ばれることがよくあります。変数が観察可能な利用可能なインスタンスを使用することで、機械学習アルゴリズムは観察されたデータからパターンと関係を学習できます。これらの学習されたパターンを使用して、変数が欠落している場合や観測できない場合の変数の値を予測できます。
期待値最大化アルゴリズムは、変数が部分的に観測可能な状況を処理するために使用できます。特定の変数が観察可能な場合、それらのインスタンスを使用してその値を学習し、推定することができます。そうすれば、観測できない場合でも、インスタンス内のこれらの変数の値を予測できます。
EM アルゴリズムは、Arthur Dempster、Nan Laird、Donald Rubin によって 1977 年に出版された独創的な論文で提案され、命名されました。彼らの研究はアルゴリズムを形式化し、統計的モデリングと推定におけるその有用性を実証しました。
EM アルゴリズムは、直接観測できないが他の観測変数の値から推測される変数である潜在変数に適用できます。これらの潜在変数を支配する確率分布の既知の一般形式を利用することにより、EM アルゴリズムはそれらの値を予測できます。
EM アルゴリズムは、機械学習の分野における多くの教師なしクラスタリング アルゴリズムの基盤として機能します。これは、統計モデルの極大尤度パラメータを見つけ、データが欠落しているか不完全な場合に潜在変数を推測するためのフレームワークを提供します。
期待値最大化 (EM) アルゴリズム
期待値最大化 (EM) アルゴリズムは、さまざまな教師なしを組み合わせた反復的な最適化手法です。 機械学習 観測されていない潜在変数を含む統計モデルのパラメータの最尤度または最大事後推定値を見つけるアルゴリズム。 EM アルゴリズムは潜在変数モデルによく使用され、欠損データを処理できます。これは、推定ステップ (E ステップ) と最大化ステップ (M ステップ) で構成され、モデルの適合性を向上させるための反復プロセスを形成します。
- E ステップでは、アルゴリズムは潜在変数、つまり現在のパラメーター推定値を使用した対数尤度の期待値を計算します。
- M ステップでは、アルゴリズムは E ステップで取得された期待対数尤度を最大化するパラメーターを決定し、対応するモデル パラメーターが推定された潜在変数に基づいて更新されます。

EMアルゴリズムにおける期待値の最大化
これらのステップを反復的に繰り返すことにより、EM アルゴリズムは観測データの尤度を最大化しようとします。これは、潜在変数が推論されるクラスタリングなどの教師なし学習タスクによく使用され、機械学習、コンピューター ビジョン、自然言語処理などのさまざまな分野に応用されています。
期待値最大化 (EM) アルゴリズムの重要な用語
期待値最大化 (EM) アルゴリズムで最も一般的に使用される重要な用語の一部は次のとおりです。
- 潜在変数: 潜在変数は、観察可能な変数への影響を通じて間接的にのみ推論できる、統計モデル内の観察されない変数です。それらは直接測定することはできませんが、観察可能な変数への影響によって検出できます。尤度: モデルのパラメーターが与えられた場合に、特定のデータが観察される確率です。 EM アルゴリズムの目標は、尤度を最大化するパラメーターを見つけることです。対数尤度: 観測データとモデル間の適合度を測定する尤度関数の対数です。 EM アルゴリズムは、対数尤度を最大化しようとします。最尤推定 (MLE) : MLE は、モデルが観測データをどの程度よく説明するかを測定する尤度関数を最大化するパラメータ値を見つけることによって統計モデルのパラメータを推定する方法です。事後確率: ベイズ推論のコンテキストでは、EM アルゴリズムを拡張して最大事後 (MAP) 推定値を推定することができます。この場合、パラメーターの事後確率は事前分布と尤度関数に基づいて計算されます。期待 (E) ステップ : EM アルゴリズムの E ステップは、観測データと現在のパラメーター推定値に基づいて、潜在変数の期待値または事後確率を計算します。これには、各データ ポイントの各潜在変数の確率を計算することが含まれます。最大化 (M) ステップ: EM アルゴリズムの M ステップは、E ステップから得られる期待される対数尤度を最大化することによってパラメーター推定値を更新します。これには、通常は数値最適化手法を使用して、尤度関数を最適化するパラメーター値を見つけることが含まれます。収束: 収束とは、EM アルゴリズムが安定した解に到達したときの状態を指します。これは通常、対数尤度またはパラメータ推定値の変化が事前定義されたしきい値を下回るかどうかをチェックすることによって決定されます。
期待値最大化 (EM) アルゴリズムの仕組み:
期待値最大化アルゴリズムの本質は、データセットの利用可能な観測データを使用して欠損データを推定し、そのデータを使用してパラメーターの値を更新することです。 EM アルゴリズムを詳しく理解しましょう。

EM アルゴリズムのフローチャート
- 初期化:
- 最初に、パラメータの初期値のセットが考慮されます。不完全な観測データのセットは、観測データが特定のモデルから得られたものであるという前提でシステムに与えられます。
- 観察されたデータと現在のパラメーター推定値に基づいて、各潜在変数の事後確率または責任を計算します。
- 現在のパラメーター推定値を使用して、欠落しているデータ値または不完全なデータ値を推定します。
- 現在のパラメーター推定値と推定欠損データに基づいて、観測データの対数尤度を計算します。
- E ステップから得られる予想される完全なデータの対数尤度を最大化することにより、モデルのパラメーターを更新します。
- これには通常、最適化問題を解決して対数尤度を最大化するパラメータ値を見つけることが含まれます。
- 使用される具体的な最適化手法は、問題の性質と使用されるモデルによって異なります。
- 反復間の対数尤度またはパラメーター値の変化を比較して、収束しているかどうかを確認します。
- 変化が事前定義されたしきい値を下回っている場合は、停止してアルゴリズムが収束したとみなします。
- それ以外の場合は、E ステップに戻り、収束が達成されるまでプロセスを繰り返します。
期待値最大化アルゴリズムの段階的な実装
必要なライブラリをインポートする
Python3
import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> |
>
>
2 つのガウス成分を含むデータセットを生成する
Python3
# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()> |
>
Javaのintから文字列へ
>
出力 :

密度プロット
パラメータの初期化
Python3
# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> |
>
>
EMアルゴリズムを実行する
- 指定されたエポック数 (この場合は 20) の間反復されます。
- 各エポックで、E ステップは各コンポーネントのガウス確率密度を評価し、対応する比率で重み付けすることによって責任 (ガンマ値) を計算します。
- M ステップは、各コンポーネントの加重平均と標準偏差を計算することでパラメータを更新します。
Python3
# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> |
>
>
出力 :

エポックと対数尤度
最終的な推定密度をプロットする
Python3
# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> |
>
>
出力 :
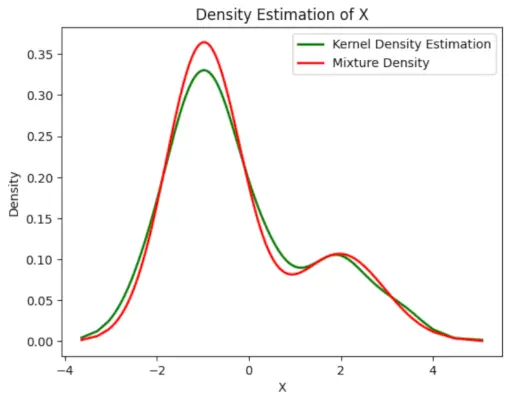
推定密度
のアプリケーション EMアルゴリズム
- サンプル内の欠落データを埋めるために使用できます。
- クラスターの教師なし学習の基礎として使用できます。
- これは、隠れマルコフ モデル (HMM) のパラメーターを推定する目的で使用できます。
- 潜在変数の値を発見するために使用できます。
EMアルゴリズムの利点
- 反復のたびに可能性が増加することが常に保証されます。
- E ステップと M ステップは、実装の点で多くの問題に対して非常に簡単であることがよくあります。
- M ステップの解決策は、多くの場合、閉じた形式で存在します。
EM アルゴリズムの欠点
- 収束が遅いです。
- 局所最適化のみに収束します。
- 前方と後方の両方の確率が必要です (数値最適化には前方確率のみが必要です)。
